采用压电波动法的水下消能爆破损伤特征试验研究*

熊 伟，钟冬望，严爱国，司剑峰，王鹏宇，刘振标

(1.武汉科技大学 理学院，武汉 430065；2.湖北省智能爆破工程技术研究中心，武汉 430065；3.中铁第四勘察设计院集团有限公司，武汉 430063)

在桥梁、大坝、围堰拆除等水下基础设施建设过程中，通常会涉及大量的水下钻孔爆破开挖工程。在岩石的钻爆开挖过程中，由于爆炸应力波的作用，在爆破完毕后，开挖轮廓线下岩体和周围保留岩体会新生许多裂纹，加上原有的微裂纹被扩大，导致这些区域岩体的力学性质劣化。这些由于爆破损伤所致的力学性质的劣化将会导致岩体完整性和稳定性受到影响，给保留岩体及岩体建基面上的构筑物安全造成了极大的安全隐患。因此，岩石爆破开挖过程中的爆破损伤监测和控制是岩石工程中的关键技术问题，它对爆破设计理论及岩体建基面稳定性分析具有重要的指导意义。为了减少爆破开挖中的损伤范围，必须采用控制爆破技术。经过数十年的工程实践经验，逐渐延伸出了一系列的爆破开挖技术，例如分层爆破开挖技术，水平预裂爆破技术，水平光面爆破技术，带垫层的台阶爆破技术等[1]。但这些技术在水下工程中往往无法使用，或者因为施工复杂导致开挖效率不高。考虑到这些因素，卢文波和胡皓然等提出了一种在垂直钻孔底部安装反射装置的爆破技术(消能爆破技术)[2,3]，用于坝基的快速挖掘。通过现场试验表明，该技术能够有效的减少岩体基础的动力破坏，并且工艺简单便捷。

爆破引起的损伤检测可以通过实测的震动位移、质点峰值振动速度或加速度值来确定。但这些方法都是根据经验得到的安全阈值，并不能直接判断爆破损伤大小。近年来，通过声波速度变化直接判断岩体爆破损伤的方法被广泛使用，研究人员基于该方法做了大量的研究。Lai等采用超声速度法检测超高性能混凝土在不同深度反复穿透和爆炸下的损伤[4]。Zhang Y Z等发现[5]，使用P波上升时间可以相对容易地区分损伤区域。但声波测量损伤的方法是依据时差法，对于较长且宽度很小的微小裂缝，绕过裂缝末端到达的绕射波有时并不优先到达接收器，而穿过微裂缝的直达波一般情况下优先到达传感器，造成损伤识别的不准确[6]。因此，迫切需要一种新的检测技术来测量爆破荷载对岩石的损伤程度。

随着对结构损伤检测要求的不断提高，结构健康监测(SHM)得到了迅速的发展，压电陶瓷传感器(PZT)在结构健康和损伤检测中得到了广泛的应用。它们具有低成本、宽频带频率响应、能量收集能力以及即可作为执行器也可用作传感器的功能[7]。压电传感器被用来直接测量结构的加速度、应变和声速[8]。同时，PZT传感器也广泛用于监测和检测静态荷载、冲击荷载和动态荷载下混凝土结构的损伤、钢筋混凝土结构中钢筋的腐蚀、混凝土的早期加固和水化以及钢筋和混凝土之间的界面脱粘[9]。Kong等人利用压电陶瓷智能骨料研究了拟动力荷载作用下钢筋混凝土桥柱的开裂问题[10]。蔡路军等利用PZT压电智能骨料监测了高强度混凝土板在爆炸荷载作用下的内部损伤情况[11]，发现小波包能量损伤指数能够良好的反映混凝土结构的损伤状况。目前，基于压电陶瓷传感器在爆破损伤检测方面的研究相对较少，特别在水下爆破方面，相关研究成果更少。

本文拟结合压电波动法的结构健康监测技术，展开水下消能爆破条件下岩体损伤状态研究。结合水介质爆炸容器进行水下消能爆破及水下常规钻孔爆破模型试验，利用压电信号研究岩体模型的损伤状态，分析消能爆破技术在水下工程中的作用。

1 试验方案

1.1 模型及测点

本次试验浇筑了一批长方体混凝土模型，其长宽高分别为245 mm、245 mm、300 mm，并在其顶部中心预留直径为12 mm，高为100 mm的炮孔。模型的物理力学参数如表1所示。

表 1 混凝土模型物理力学参数Table 1 Physical and mechanical parameters of concrete model

在混凝土模型养护好以后，在其相对的两个面上用油漆标记了20个损伤测试点，具体为水平方向上每49 mm一个点共四个点(1～4)，垂直方向上每50 mm一个点共5个点(A～E)，浇筑后模型的标记示意图如图1所示。

1.2 基于压电波动法的损伤检测

将损伤测试点标记好后，基于波动法，在爆破前，利用压电信号采集与分析系统测试混凝土模型的健康状况。用于激励的信号为脉冲信号，其幅度，脉冲宽度，持续时间和编码位分别为100 V，15 μs，30 μs和2，如图2所示。

图 1 损伤测试点标记示意图Fig. 1 Schematic diagram of damage test point marking

图 2 用于激励的脉冲信号Fig. 2 Pulse signal for excitation

图3所示为本次试验所用的压电陶瓷测试与分析系统。测试时，用凡士林将图中的2个PZT贴片耦合到对应的损伤测试点上，PZT连接采集仪，采集仪通过六类网线连接PC端。通过电脑控制采集仪激励脉冲信号，同时，用于接收的传感器将收到的信号传输到PC端。

图 3 压电信号采集与分析系统Fig. 3 Piezoelectric signal acquisition and analysis system

1.3 模型试验装药结构

消能爆破技术首先将一层松软细沙垫在炮孔底部，再在松砂上装入由铸铁或高波阻抗混凝土材料制作成的消能球，最后进行常规装药和堵塞[12]。图4为其具体装药结构及炸药爆炸产生应力波的反射透射示意图[13]。

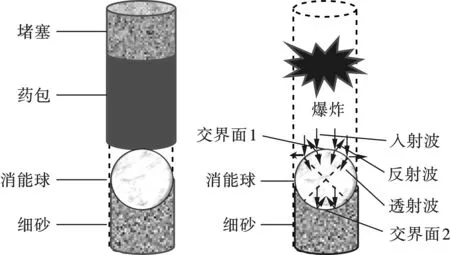
图 4 消能爆破技术的装药结构及 应力波反射透射示意图Fig. 4 Charge structure and stress wave reflection and transmission of energy-relief blasting technique

根据应力波反射透射理论，以一束一维应力波的传播为例，当应力波从一种介质传播到另一种介质时，将在分界面发生反射和透射，其反射透射系数可用下式表示[14]

(1)

(2)

式中：I为入射应力波强度；R为反射波强度；T为透射波强度；ρCp为材料的波阻抗。

在炮孔内炸药爆轰的瞬间，如图4所示，由于炮孔内爆生气体、消能球以及消能球下方的细沙波阻抗各不相同，爆炸波将在交界面1和交界面2发生多次反射和透射。首先，由于消能球和爆生气体的波阻抗不同，在交界面1会发生应力波的反射和透射，部分被反射回上部岩体中，部分被透射到消能球内。这些透射到消能球内的应力波在交界面又会再次发生反射和透射，造成透射到炮孔下方岩体的应力波被大幅削弱，有效的减少了炮孔底部岩体的损伤。

选3个模型进行消能爆破技术的装药，首先在炮孔中垫一层10 mm厚的细沙，再加入直径为10 mm的消能球，本次试验中使用的消能球为轴承钢珠。另一个模型采用常规装药，在底部同一高度直接装药堵塞，具体的模型编号如表2所示，实际的装药结构如图5所示，其中起爆用的雷管按照1 g药量计算。

表 2 模型实验方案一览表Table 2 List of model experiment schemes

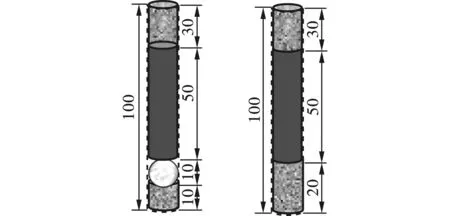
图 5 实际装药结构示意图(单位：mm)Fig. 5 Schematic diagram of the actual charge structure(unit:mm)

1.4 水下爆破环境

借助200 m水深水介质爆炸容器，装药完成后，将模型放入水介质爆炸容器中，并将导爆管做好防水处理连接到容器的装药口。通过向容器内注满水并加压到0.4 MPa模拟40 m水深，加压完成后，在装药口连接起爆线，进行40 m水深水下钻孔爆破试验。图6为试验所用的水介质爆炸容器。

图 6 水介质爆炸容器Fig. 6 The water medium explosion vessel

爆破完成后，泄压排水，取出试样，待试样晾干后，采用和爆前一致的压电波动法对模型试样进行结构健康监测。

2 试验结果

爆破完成后，试样在宏观上都表现出了很明显的损伤，如图7所示。相同药量的试样F5和F6在表面上的损伤并没有表现出明显的区别。但随着药量的增大，试样在宏观上的损伤变得明显。在仅有1 g药量的情况下，试样F4仅能观察到非常微小的裂纹，炮孔无明显的扩大但附近有小块崩落；在药量为3 g时，试样F5和F6都会出现明显的贯穿到试样边界的“米”字型裂纹；在药量为5 g的情况下，试样F1也存在贯穿边界的裂纹且出现了明显的爆破漏斗。

图 7 爆破后试样的宏观损伤情况Fig. 7 Macroscopic damage of specimens after blasting

在爆破前后，分别利用压电信号采集与分析系统，对每个试样上标记的损伤测试点进行基于波动法的结构健康监测。图8(左：爆前；右：爆后)列出了爆破前后每个试样上A2、C2、E2三个典型测试点的压电信号。

从图8可以看出，在爆破前，测点上都能接收到比较良好的压电波形，说明混凝土材料在爆破前是一种良好的应力波传导介质。由于混凝土材料在浇筑的时候很难达到理想的均质状态，不同测点压电信号的波形也存在一定的差异。爆破后，原始裂纹被扩大且伴随着新裂纹的产生，阻碍了应力波的传播，导致相同测点在爆破后的信号幅值都会衰减。且在炮孔附近的A2、C2测点衰减十分明显，但在试样相对底部的E2测点则衰减很小。

图 8 爆破前后A2、C2、E2测试点的压电信号Fig. 8 Piezoelectric signals of A2、C2、E2 test points before and after blasting

3 结果分析

在利用波动法的结构损伤识别分析中，较为常用的损伤计算方法有时差分析法、时域分析方法和频域分析方法等。本文通过分析比较爆前爆后接收信号在一定时域的能量得到相应测点的损伤指数。若信号x(t)为接收信号传感器采样所获得的一组离散数据，该信号的能量表达式为

(3)

式中：i为该时域内的采样点个数、xi为对应采样点的电压幅值。通过比较爆前的信号能量Epre得到的岩体在爆破荷载作用下的损伤指数为

(4)

为了进一步分析水下钻孔爆破作用下混凝土岩体的损伤，根据式(4)，计算了不同混凝土试样在爆破后的损伤因子。将20个损伤测试点的损伤因子绘制成图9所示的三维矩阵图，可以明显的发现，每个试样的炮孔部分损伤明显大于炮孔以下部分，且每个试样上的大部分测点越接近炮孔的损伤越大，即损伤与该点和炮孔的距离成反比。

图 9 4个试样各测点损伤情况Fig. 9 Damage of each measurement point of four specimens

为了了解不同药量的损伤情况，计算了3个相同装药结构情况下试样炮孔部分和炮孔以下部分两个区域内计算得出的损伤因子的平均值，通过损伤因子的均值来判断损伤随药量的变化情况。图10为试样上下两个部分损伤因子随药量的变化情况。

图 10 试样上下两部分损伤因子随药量变化Fig. 10 The damage index of the upper and lower parts of specimen changes with the charge

通过图10可以看出，试样的损伤和药量存在明显的关系。在药量从1 g增加到3 g时，炮孔部分的损伤增加了160.57%，而炮孔底部的损伤增加了34.23%。此时炮孔底部损伤增加的幅度较炮孔部分要小很多。当药量继续增加到5 g时，炮孔部分的损伤仅增加了1.11%，而炮孔底部的损伤增加了79.87%。即在药量为3 g时，试样的炮孔部分已经基本被完全损伤，但试样底部的损伤相对较小，导致药量继续增加时，试样底部的损伤增加的幅度较大。综合来看，试样的损伤随着药量的增大而增大，且药量为3 g时的试样炮孔部分已基本被完全破坏。

基于压电波动法，通过试样整体的损伤分布情况和损伤因子随药量的变化情况分析，发现损伤分布和随药量的变化和已知的规律十分一致，这说明基于压电波动法的水下钻孔爆破损伤测试方法是可行的。

为了进一步分析水下消能爆破技术的损伤控制效果，分析了在相同药量的情况下，采用常规爆破技术的F6试样和采用消能爆破技术的F5试样的损伤分布区别。

图11为F5和F6两个试样从上至下“A～E”五排测点的平均损伤因子变化趋势。可以看出，在炮孔部分，两个试样的损伤值并无明显区别；但采用消能爆破技术的试样在D排测点的损伤因子衰减幅度的要明显大于采用常规爆破试样。计算了炮孔以下“D”,“E”两排八个测点损伤因子的平均值，发现使用消能爆破技术的试样平均损伤值比常规爆破要小33%。说明消能爆破技术在水下钻孔爆破中同样具有良好的效果。

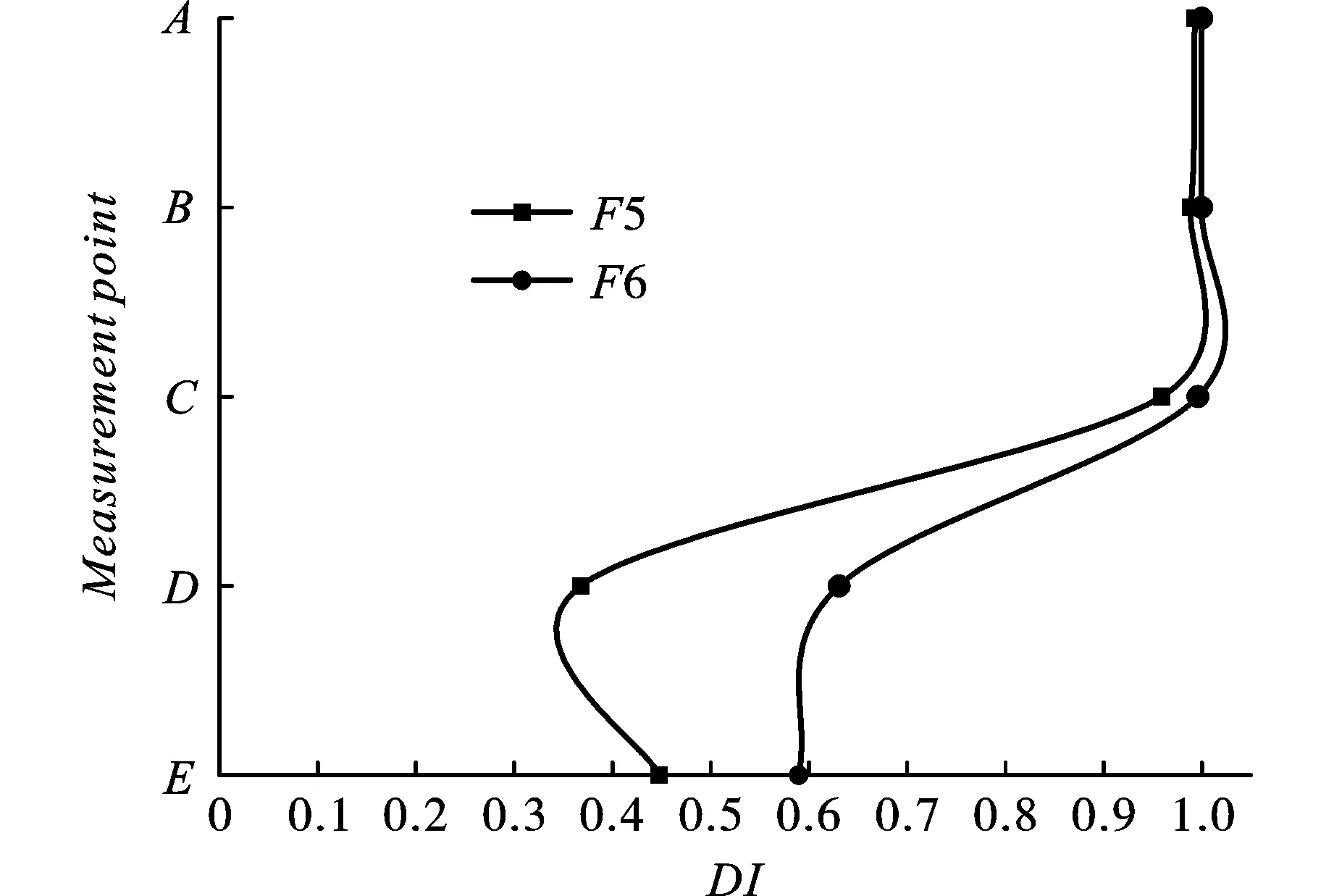
图 11 每排测点平均损伤因子变化图Fig. 11 Change graph of average damage index for each row of measurement points

从图9和图11中都可以发现，最后一排的损伤因子出现反弹现象，这是爆炸压缩波在试样边界反射为拉伸波造成的二次损伤以及爆破振动使试样底部与容器发生碰撞产生的二次损伤导致，这也是模型试验的局限性。

4 结论

通过对混凝土岩体模型进行不同条件的水下钻孔爆破试验，并结合基于波动法的压电陶瓷损伤检测技术检测试样的损伤，主要得出以下结论：

(1)对于所有的试样，所有试样某一点的损伤与该点到炮孔的距离成反比。试验得出的损伤因子分布与实际观测到的损伤分布相关性较好，采用波动法结合能量分析得出的损伤因子能够比较准确的体现水下钻孔爆破产生的损伤。

(2)水下钻孔爆破损伤随药量的增加而增加，且本实验中所使用的混凝土模型炮孔部分在药量为3 g时已基本被完全破坏。

(3)在基底部分的两排测点，使用消能爆破技术的试样平均损伤因子比常规爆破要小33%，这说明消能爆破技术在水下钻孔爆破中具有良好的损伤控制效果。

(4)爆破引起的试样振动和边界效应会在试样的边界处造成一定程度的二次损伤。