防暴弹室内爆炸扩散试验及刺激剂浓度预测*

张延泽，肖凯涛，宋伟伟，秦 健，迟 卉，黄瑞源

(1.南京理工大学 瞬态物理国家重点实验室，江苏 210094；2.福州大学 土木学院，福州 350000；3.防化研究院，北京 102205；4.海军研究院，北京 100161)

鉴于恐怖暴乱活动日显猖獗，严重影响国家的政治稳定和经济发展，目前反恐防暴已经成为一项严峻、迫切、长久、持续的特殊任务。能否确保对室内非法集结及恐怖暴乱形势进行迅速、有效地控制，并能最大程度上减少人员伤亡，需要警务人员在执行不同级别制乱任务时，使用不同类型的反恐防暴装备[1-4]。刺激剂防暴弹是反恐防暴中一种常用武器，警务人员在处置突发事件和反恐防暴中，根据特定情况需要，会向室内或者相对密闭的空间内以爆炸式防暴弹形式施放刺激剂，用以震慑控制恐怖暴乱分子。对刺激剂防暴弹室内爆炸扩散的威力效能进行评估能够为该武器的合理使用提供理论依据。

刺激剂具有达到战斗浓度的药剂用量少、症状出现和消失快、具有很高的安全比和可用多种弹药器材释放等优点[5,6]，早在第一次世界大战和美越战争时已经被广泛使用。目前国内外学者主要从试验研究、理论分析和数值模拟三个方面开展刺激剂防暴弹爆炸扩散非致命效能方面的研究。Noh等通过实验和数值模拟的方法对洁净室内颗粒物浓度分布进行了研究[7]，结果发现颗粒物浓度与排风量和送风位置有很大关系。Sharon等在室外开展了不同气象条件下脏弹爆炸烟云实验[8]，提出了云顶预估模型。Posner等采用CFD方法模拟得到实验室条件下烟雾的流动受障碍物的影响很大[9]。Shi Guangshan等提出了一种由大孔和基质组成的双介质概念模型[10]，对瓦斯扩散进行了实验及数值模拟研究。段中山等对TNT爆炸烟云在大气中扩散的时空分布进行了试验及仿真研究[11,12]，得到了烟云扩散形态演变过程和爆炸烟云扩散高度分布模型；谢朝阳等开发了大气中炸药爆炸气溶胶扩散数值计算程序[13]，用于快速预测炸药爆炸事故引发气溶胶扩散的浓度分布。程万影等对空中两米处的新型控暴器材进行爆炸分散研究[14]，采用隐形示踪剂和采样分析的试验手段，得到了单发弹静爆后形成的威力幅员和作用时间。王晓华研究了可燃气体室内的扩散特性[15]，蒋裕平等则对甲醛的室内扩散特性进行了模拟研究[16]；欧阳的华等采用Fluent软件对催泪剂的室内扩散特性进行了模拟研究[17]。刘志龙等在爆炸室内对短切碳纤维开展了空中爆炸分散试验[18]，获得了壳体破裂、云团特征，得出云团参数变化规律及相似律。已有的研究结果表明：目前相关研究主要针对颗粒及气体扩散，并且对目标物爆炸后云团的形成过程及扩散特性的研究主要集中在室外环境下，而对于刺激剂防暴弹室内爆炸扩散及威力评估的研究较少。由于室内环境与室外环境相比，初始风场及壁面效应对于刺激剂云团的形成及扩散迁移运动的影响很大，将室外环境下的研究成果应用于室内防暴弹的威力评估并不合适。

基于上述问题，开展了室内环境下刺激剂防暴弹爆炸扩散试验，并通过改变送风口风速实现不同初始流场条件下刺激剂气溶胶扩散的物理过程。通过室内空间中36个采样点，测得不同时间不同空间位置的刺激剂浓度。采用Matlab软件对室内空间中的浓度分布进行三维拟合，分析空间中不同位置的刺激剂浓度随时间变化的规律，同时定量分析不同送风条件对空间中不同位置刺激剂浓度的影响规律。在此基础上，以送风速度、时间和空间坐标为输入，以刺激剂浓度为输出，采用BP神经网络方法对试验数据进行训练，建立刺激剂浓度预测模型，对一定送风速度范围条件下刺激剂防暴弹室内爆炸扩散的刺激剂浓度分布进行预测，从而为刺激剂防暴弹药的有效威力效能评估提供实验数据和理论依据。

1 爆炸扩散试验

1.1 试验场地与测点布局

试验在某平房(见图1)内进行，平房尺寸为10.9 m(长)×9.1 m(宽)×3.28 m(高)，在东侧墙壁高度2 m处设有3个送风口(见图2)，西侧墙壁下方距地面0.15 m处设置3个回风口。

图 1 试验场地 Fig. 1 Experiment site

图 2 平房内部Fig. 2 Bungalow interior

试验对空间内的36个点进行了浓度的测定。测点位置：取长度方向的五等分点4个，宽度方向的四等分点3个，高度方向3个(0.5 m、1.5 m、2.5 m)，总测点个数共计4×3×3=36个。测点位置见图3，并采用如图4所示方式对同一高度平面内的测点进行编号。见图3、图4。

图 3 测点位置Fig. 3 Measuring locations

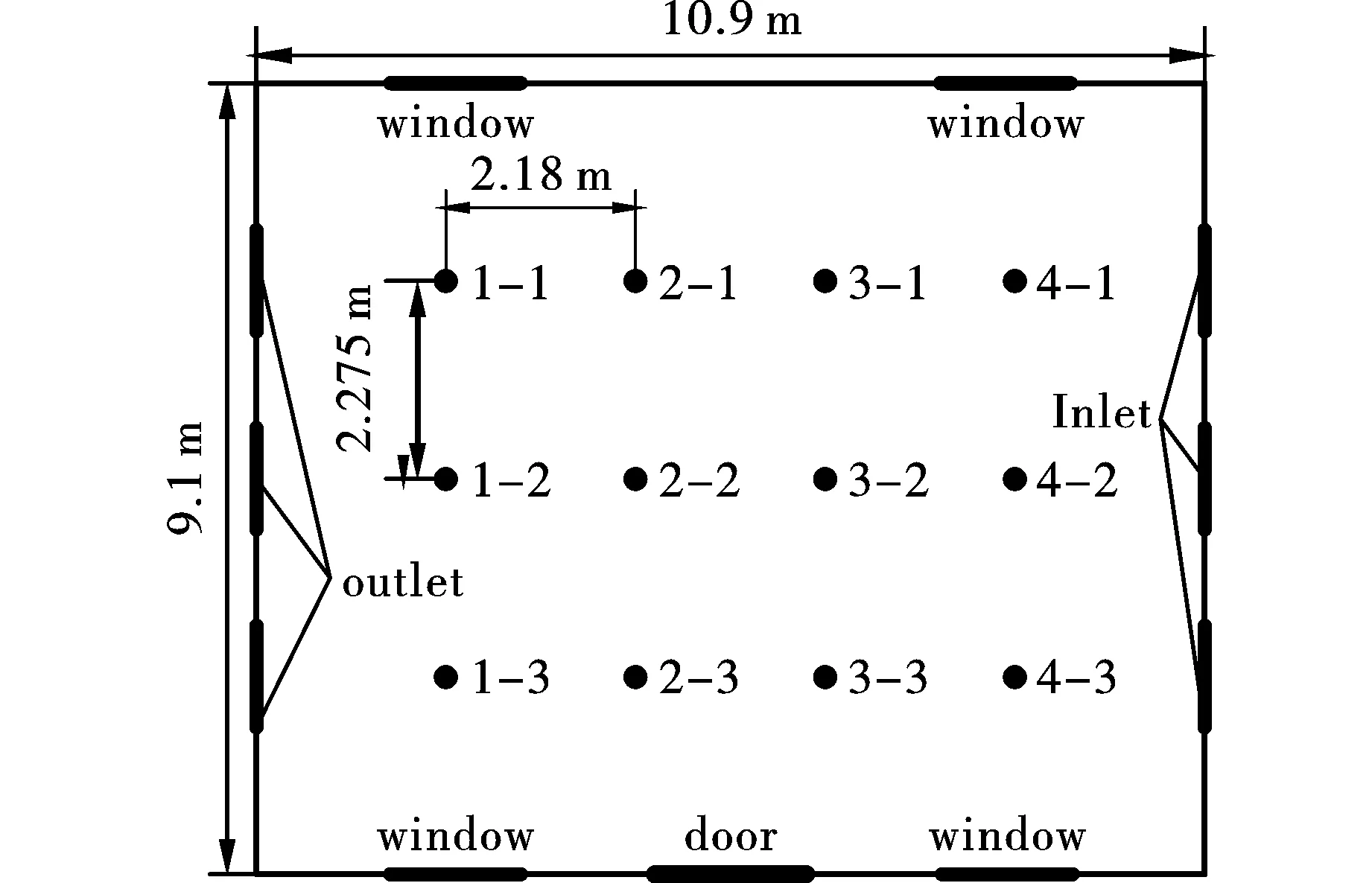
图 4 测点位置平面示意图Fig. 4 Plan sketch of measuring points

1.2 数据采集及处理

试验采用电风扇送风，电风扇的转动频率采用低中高三档进行调节，其频率分别为20 Hz、30 Hz、40 Hz，对应的风速分别为1.0 m/s、1.2 m/s和1.5 m/s。为保证试验准确性，在相同风速下分别进行了三次重复试验，经风速仪测得送风口处同一风速下的试验结果具有较好的重复性。在送风速度为1.0 m/s、1.2 m/s和1.5 m/s条件下分别进行3次重复爆炸扩散试验，共9组试验，弹药均在建筑空间中心高度为1.5 m处爆炸。

测试系统由智能多路气体采样器、智能采样器和空气动力学粒径谱仪组成。通过调节采样器控制流量及采样时间，采样器流率为6 L/min，采样原理为经采样头采集刺激剂，通过粒径谱仪测定气溶胶颗粒的空气动力学粒径，从而给出气溶胶数量浓度、表面积浓度、体积浓度以及质量浓度随粒径的分布情况[3]。

从弹药燃爆开始计时，分别在30 s、90 s、150 s时刻启动采样器进行采集，采样时间为1 min，取1 min内平均浓度。记爆炸后时间t在30～90 s对应t1，90～150 s对应t2，150～210 s对应t3。试验结束10 min后，进入试验区取下采样头依次进行去壳、取膜、加液、超声、沉淀处理，并送至分析实验室采用液相色谱法进行定量分析[19]。采样器采集刺激剂时依赖泵吸作用，具有一定的抽吸力，采样系统具有自动补偿功能，经采样得到的OC浓度即为大气中该点处的实际浓度值。按(1)式计算出每个采样点上的平均浓度值。

(1)

式中：c为采样时间Δt内的平均浓度，mg/m3；gz为采样头所采集的刺激剂样品量，mg；V是采样体积，m3；Q为采样器流量，m3/s；Δt为采样时间，s。

对于同种工况的三组数据进行处理时，采用了格拉布斯法[20-23]，数据处理过程如下。

(2)

(3)

接着计算Gi值

(4)

将Gi值与格拉布斯原则给出的临界值GP(n)比较，如果计算的Gi值大于临界值GP(n)，则能判断该测量数据是异常值，可以剔除。对于三次试验(n=3)置信概率P=0.95的G0.95(3)=1.153。剔除异常值后，求出均值。

1.3 试验结果分析

1.3.1 送风速度为1.2 m/s时浓度分布

采用MATLAB软件，将送风口送风速度为1.2 m/s条件下爆炸浓度扩散试验各测点数据绘制成三维曲面。采用插值逼近的方法，将三维坐标中的数据离散点采用重调和方程四阶偏微分方程近似成光滑曲面，可以近似得到试验空间中某一高度平面内刺激剂浓度值的大致分布，结合等值线可以分析出浓度分布的规律。图5给出了送风速度v=1.2 m/s时，弹药爆炸后不同时间段(t1、t2、t3)的浓度平均值在不同高度(0.5 m、1.5 m、2.5 m)水平面内的分布。图中x、y为测点在水平面内的坐标；z轴表示浓度值，单位为mg/L；箭头所示方向表示吹风方向。

图 5 不同高度测点浓度分布(v=1.2 m/s)Fig. 5 Concentration distribution at different heights(v=1.2 m/s)

在风场的作用下，同一水平面内的12个测点浓度大致呈阶梯分布，由上风口到下风口浓度值依次升高，其原因是刺激剂自由扩散的同时受风场影响，上风口处的气溶胶颗粒在风场作用下向下风口处飘散聚集。从时间上看，这种浓度梯度差随时间的延长而减小，整体浓度值趋于大致相同。由于墙壁处的壁面效应，使得刺激剂在随气流吹散到出风口墙壁处时造成回流并形成涡旋，部分刺激剂气溶胶颗粒由出风口墙壁处回旋至房间中心，从而使房间内部刺激剂浓度分布随时间变化越来越均匀。从高度上看，1.5 m高度处各点的浓度值普遍较高，0.5 m高度处的浓度值次之，2.5 m高度处的浓度值最低，这是由于1.5 m高度处是爆炸中心位置，爆炸初始浓度较高。另一方面爆炸后一些较小的刺激剂气溶胶颗粒相互吸附聚集形成较大的颗粒团，刺激剂气溶胶颗粒平均空气动力学直径为10 μm，受重力作用进行沉降，逐渐向低处聚集并形成较高的浓度。从整体浓度分布趋势可以发现，室内通风条件下刺激剂防暴弹的爆炸位置靠近送风口且高度在1.5 m以上时能够发挥较大的震慑威力，警务人员使用防暴弹时，应考虑室内通风系统中的送回风口位置以及投放高度。

1.3.2 高度1.5 m处不同送风条件的浓度分布

选取高度1.5 m处不同风速下的浓度数据探究送风速度的大小对浓度分布规律的影响。

由于测试系统原因，当v=1.0 m/s和v=1.2 m/s时“测点1～3”处采样器未测出浓度数值，在拟合浓度分布三维曲面时，将该点排除，如图6中(a)～(c)和(g)～(i)图中画红色“×”的位置所示。可以看出，浓度值呈上风口浓度低于下风口浓度。并且随着送风速度的增加，这种浓度差有越来越大的趋势。

图 6 不同风速下浓度分布(h=1.5 m)Fig. 6 Concentration distribution under different wind speeds (h=1.5 m)

当v=1.0 m/s时，爆炸扩散开始后t1时间内(图6(a))，上风口浓度略高于下风口。一方面是刺激剂爆炸后形成的气溶胶初始云团的浓度分布不均匀，另一方面是由于风速过低，风力过小，导致气溶胶颗粒受风的作用较小，随着时间的延长，气溶胶颗粒扩散运动受风场的影响越来越明显。在t2时段(图6(b))，水平面内的浓度值分布较为均匀。当t3时(图6(c))，可以看到，呈下风口浓度值偏高的分布状态。当v=1.2 m/s时，可以看出，在风场的影响下，刺激剂浓度在水平面内的分布较为均匀。当v=1.5 m/s时，从爆炸扩散前期开始就有下风口的浓度聚集现象，并且浓度梯度差相对较大。这是由于风力过强，气溶胶颗粒受风场的作用较大，扩散较快，导致水平面内上、下风口处浓度差偏大，浓度最大值为8.19 mg/L，与最小值0.12 mg/L相差67倍。分析送风速度对刺激剂浓度分布的影响，可以看出风速大小对于刺激剂浓度扩散速度影响较大，针对本试验条件而言，送风速度为1.2 m/s时，刺激剂浓度在空间中分布均匀，没有产生局部浓度过高或过低的现象。刺激剂浓度过高会对人员造成过度伤害，浓度过低又不能起到控制的作用。刺激剂防暴弹在实际投放时，应考虑使用场景中气流的影响，必要时增加送风设备以营造适合的流场环境，充分发挥刺激剂防暴弹的威力效能。

1.3.3 风速对刺激剂浓度值的影响

图7对比了风速为1.0 m/s、1.2 m/s、1.5 m/s时测点的浓度值，高度为0.5 m和1.5 m的各测点浓度值均随着送风速度的增加而降低。当高度为0.5 m时，三种风速下测点平均浓度分别为2.37 mg/L、2.14 mg/L和1.36 mg/L，可以看出风速对浓度值分布的影响较大。一定范围内风速越大，房间内流场运动越快，刺激剂气溶胶向房间外部的扩散运动越剧烈，导致房间内浓度整体水平降低。但对于部分测点，如高度为0.5 m的测点1-1和测点3-3、高度1.5 m的测点3-3、4-2和4-3，其浓度值在v=1.2 m/s时最高。上述测点位置均靠近墙角处，v=1.2 m/s时室内形成涡流场，致使墙角附近处的刺激剂颗粒持续聚集累积，形成较高的浓度。

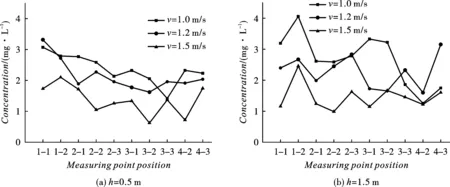
图 7 不同风速下测点浓度值(t=t3)Fig. 7 Concentration value of measuring point under different wind speeds(t=t3)

1.3.4 刺激剂浓度值随时间变化

对于送风速度1.5 m/s的条件下(见图8)，各测点浓度值随着时间的延长而降低，浓度分布随时间变化越来越均匀。高度为2.5 m(图8(c))的大部分测点在t1、t2、t3时浓度平均分别为2.43 mg/L、1.67 mg/L、1.20 mg/L。测点1-1和测点1-2浓度值随时间变化较大，测点1-1在t1、t2、t3时段浓度值为其他测点的1.2～3.6倍，测点1-2在三个时段的平均浓度为其他测点的2.2～4.2倍。造成浓度差较大的原因是其位置距出风口较近，在较大风力(v=1.5 m/s)的作用下，刺激剂气溶胶颗粒向出风口处聚集形成较高的浓度。

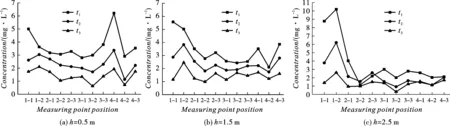
图 8 不同时间段各测点浓度对比(v=1.5 m/s)Fig. 8 Concentration comparison of each measuring point in different time periods(v=1.5 m/s)

为进一步说明刺激剂浓度值随时间下降快慢受风速的影响，给出了高度1.5 m的测点1-1浓度时程曲线，如图9(a)所示。在1.0 m/s和1.5 m/s风速下，测点1-1的刺激剂浓度值随时间变化基本呈线性降低，t1时段到t3时段浓度分别下降了62%和79%，当风速为1.2 m/s，t1到t2时浓度下降了59%，t1到t2时浓度下降只有5.3%，这表明1.2 m/s风速下室内流场在爆炸1.5 min后浓度场较为稳定，刺激剂浓度值缓慢下降。风速1.2 m/s下测点2-2不同高度浓度时程曲线如图9(b)所示，爆炸后t1时段该点在1.5 m高度处有较高的刺激剂浓度，而高度2.5 m处浓度较低。随时间推移，三个高度的浓度差逐渐变小，在达到时间t2后浓度均在1.35～3.81 mg/L范围内变化。可以看出该工况下刺激剂爆炸后可在1.5 m处形成较高的浓度，并且在较长时间内刺激剂浓度维持在2.8 mg/L以上。

图 9 测点浓度时程曲线Fig. 9 The concentration time history curve of the measuring point

2 BP神经网络预测

2.1 BP神经网络简介

BP神经网络(Back-ProPagation Neural Network)又称反向传播神经网络[24,25]，通过样本数据的训练，不断修正网络权值和阈值使误差函数沿负梯度方向下降，逼近期望输出。BP神经网络具有一个或多个隐含层和输出层，可以对具有有限个不连续点的函数进行逼近从而具备出现线性不可分问题的能力，是目前神经网络应用中最为广泛的神经网络模型之一[26,27]。

BP神经网络由输入层、隐含层和输出层组成，网络选用S型传递函数(式(5))，通过反传误差函数(式(6))不断调节网络权值和阈值使误差函数E达到极小。

(5)

(6)

式中：ti为期望输出；Oi为网络的计算输出。

2.2 BP神经网络参数设置

以不同送风速度、不同时间以及不同空间位置的测点浓度数据作为样本值，共有324组样本，由于试验样本采集问题，其中部分测点数据失真，总计有效样本297组。在297组样本中随机选取277组样本作为训练神经网络的训练集，10组样本作为测试网络质量的验证集，其余10组则作为测试网络预测精确度的测试集。首先分别将训练集、验证集和测试集的数据作归一化处理，使其分布于0～1之间，神经网络是以样本在事件中的统计分布率来进行训练(概率计算)和预测的，归一化的作用是统一样本在0～1之间的统计概率分布。

接着创建神经网络，输入层为影响刺激剂浓度的因素，分别为送风速度v、时间t、及空间坐标x、y、z，共五维，将其用X1，X2，…，X5表示。输出层只有一维，即为刺激剂的浓度值c，将其设为Y。

在参数调整中初选隐含层节点数按经验公式(式(7)～式(9))确定大致范围

(7)

M=log2n

(8)

(9)

式中：k为样本数;M为隐含层节点数;n为输入层节点数;m为输出层节点数;a为0～10之间的整数。

Levenberg-Marquardt(LM)算法是求解非线性最小二乘问题的一种广泛应用的方法[28]，它是牛顿法的变形，用以最小化那些作为其他非线性函数平方和的函数。1994年，Hagan等人首次把数值优化算法Levenberg-Marquardt (LM)应用到BP算法的训练[29]，以改进其收敛速度。多年来，国内外学者针对LM算法做了大量应用与改进研究[27,30-33]，其目的是提高精度，加快运算速度。对于本研究中刺激剂浓度预测问题，选用常用的LM算法，以期在快速收敛的基础上能保证较高的稳定性和精度。训练的收敛误差平方和取为1×10-5，训练的最大次数设为1000，学习速率为0.001。经过多次运行进行试值，最终确定隐含层节点数为10，迭代次数为22次，网络质量及测试结果见图10。经过训练后，BP神经网络收敛，预测值与试验值相对误差在±5%以内。将训练好的BP神经网络权值及阈值保存，以便进行接下来的浓度预测。见图10。

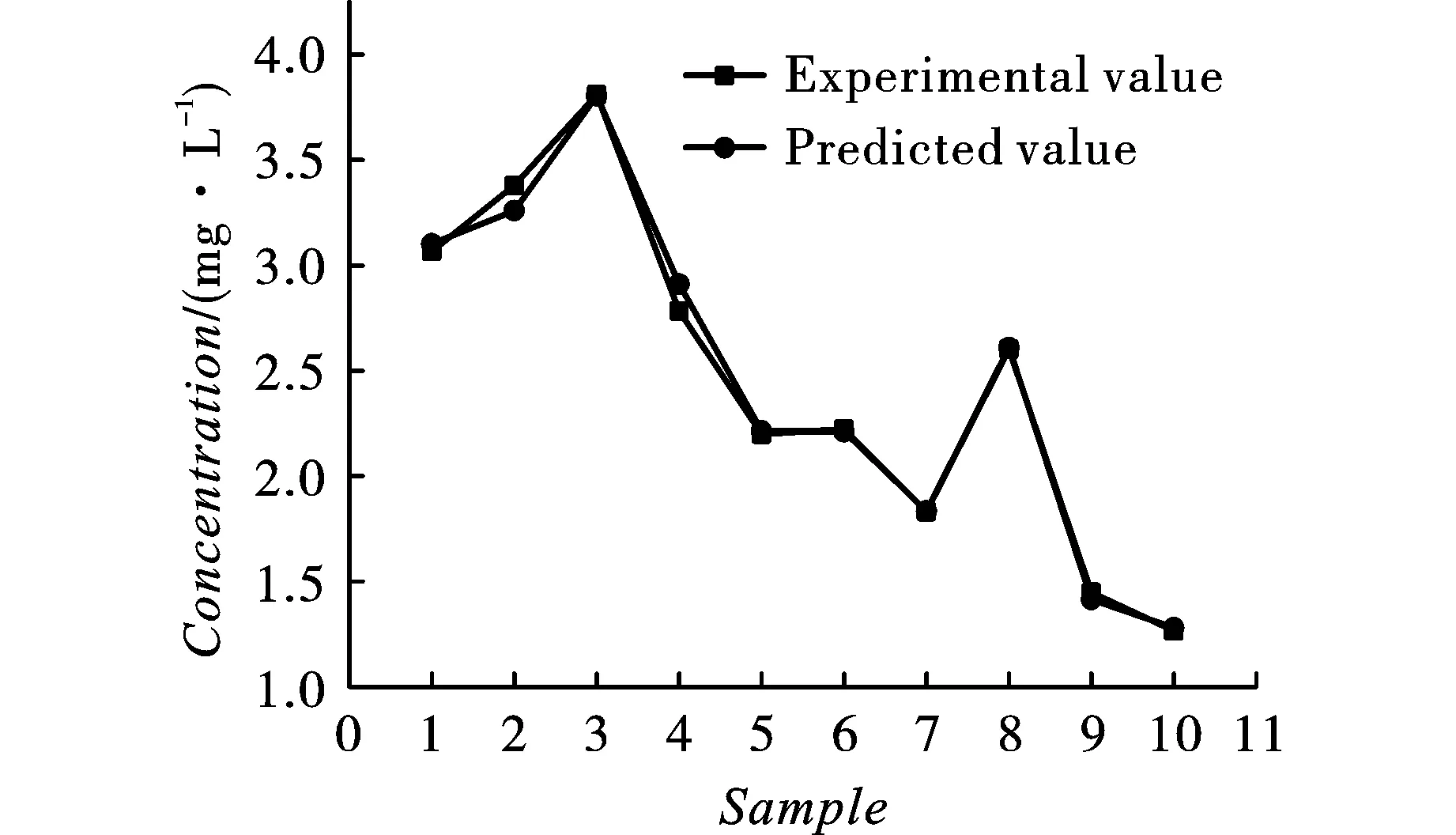
图 10 BP神经网络测试结果Fig. 10 BP neural network test results

2.3 BP神经网络预测结果

采用已建好的BP神经网络对送风速度为1.0～1.5 m/s范围内，空间中测点2-2(h=1.5 m)的浓度随时间变化情况进行预测，得到如图11(a)所示的浓度时程曲线。从曲线来看，在爆炸后30～210 s的时间段，空间中2-2测点的浓度值随时间变化呈递减趋势，且浓度值随送风口风速的增大而递减的越快。

对不同高度处的2-2测点位置预测其在爆炸后t1时浓度值随送风速度大小的变化，得到如图11(b)所示曲线。在送风速度为1～1.5 m/s的范围内，测点2-2的浓度值随风速的增加而基本呈线性降低，且高度1.5 m的测点浓度值高于高度为0.5 m的测点，2.5 m高度处的测点浓度最低。此外，为了探究浓度值随测点位置与送风口的距离的关系，对送风速度为1.2 m/s，t1时段，高度1.5 m的平面内，距离送风口2.275～6.825 m的范围内的测点浓度值进行了预测，如图12所示。从测点浓度值随距送风口距离大小变化的曲线图中，不难看出，观测点位置离送风口越近，该点浓度值越低。并且这种变化规律基本呈线性，而测点高度对该变化规律几乎无影响。

图 11 测点2-2浓度预测Fig. 11 Concentration prediction at measuring point 2-2

图 12 测点浓度值与距送风口距离大小的关系Fig. 12 The relationship between the concentration value of the measuring point and the distance from the inlet

此BP神经网络预测模型适用于本研究中提到的刺激剂防暴弹和试验场地，在送风速度为1.0～1.5 m/s范围内能够对空间中刺激剂浓度进行准确预测。

3 结论

针对刺激剂防暴弹爆炸扩散的研究以室外环境居多，室内较少的现状，采用试验结合仿真预测进行研究，通过三种不同送风条件下室内空间中刺激剂的爆炸扩散试验，得到了爆炸后刺激剂气溶胶在空间中的浓度分布规律，同时采用BP神经网络预测模型，以试验得到的不同风速下、不同时刻空间中不同位置采样点的浓度数据为训练对象建立神经网络，对一定送风速度范围内的时空浓度分布进行了预测。研究得到：

(1)基于室内环境下开展的刺激剂防暴弹爆炸扩散试验，其刺激剂浓度分布受室内初始风场条件和壁面效应的影响，刺激剂经过扩散运动及沉降吸附作用，在下风口及空间低处逐渐形成较高的浓度。在刺激剂防暴弹设计过程中，刺激剂含量应适当选取，避免局部空间刺激剂浓度过高对人员造成不必要的伤害。

(2)室内初始风场条件对刺激剂浓度时空分布影响较大，当风速为1.2 m/s时刺激剂扩散速度相对较快，同时室内刺激剂浓度分布也较为均匀，可以为刺激剂防暴弹在室内合理使用提供一定参考。

(3)以BP神经网络理论为基础，基于试验数据建立了刺激剂防暴弹室内爆炸扩散浓度预测模型，该预测模型适用于风速在1.0～1.5 m/s时室内刺激剂防暴弹爆炸扩散浓度预测问题，预测结果与试验结果进行对比，误差仅为5%，满足工程要求，可应用此预测模型对试验未开展的工况及试验难以观测的采样点进行浓度预估。