基于改进分支定价算法的ASC车辆路径问题

周 红，朱 瑾

（上海海事大学物流科学与工程研究院,上海 201306）

0 引言

自主驾驶无人跨运车(Autonomous Straddle Carrier，ASC)是一种应用在自动化集装箱码头上的移动机器人，依靠人工智能技术能够实现自主定位、自主导航、面对突发状况能够做出智能决策，并且能够自主规划出集装箱水平运输的最优路径[1]。AGV与ASC都是自动化集装箱码头上的水平运输车辆，主要的区别在于ASC不需要与岸桥和自动轨道吊直接交互，可以独立完成集装箱的装卸工作，装卸效率高。ASC的车辆路径问题就是为每台ASC寻找一条可行且高效的路径，使ASC完成一系列的集装箱转运工作。由于涉及到的作业量大、ASC数量多且码头环境复杂，ASC车辆路径问题受到越来越多的关注。

基于ASC作业的独立性，可以将ASC车辆路径问题建模为带硬时间窗的同时取送货问题（PDPTW）。关于车辆路径问题的求解算法，已经有许多学者进行了深入研究。例如，姚锦宝等[2]用改进的蚁群算法对同时取货送货车辆路径问题进行求解，贾方方等[3]采用改进的粒子群优化算法对同时取货送货车辆路径问题进行求解，陈秀娟等[4]用改进的蚁群算法求解了逆向物流中的车辆路径问题，武小平等[5]设计遗传算法求解了不确定配送条件下的车辆路径问题。文献[6，7]提出了基于禁忌搜索和导引式局部搜索的混合式启发式算法求解同时取货送货问题，文献[8]提出一种混合遗传算法求解了带硬时间窗的车辆路径问题，但这些方法都是基于近似的方法，能够得到可行解但并不是最优解。近年来关于VRP及其一系列变体问题的研究大都将其转化为大规模整数规划问题来求解。在精确算法的相关研究中，最基本的方法为分支定界算法，虽然能够从理论上保证在有限时间内获得最优解，但在实际计算中存在着计算耗时巨大的情况。Desrosiers等[9]首次提出将列生成算法与分支定界算法结合起来对车辆路径问题进行求解，Barnhart等[10]将其命名为分支定价算法。文献[11]针对自动化集装箱码头ASC的车辆路径问题，以车辆运输成本最低为目标建立优化模型，提出了一种基于分支定界和列生成算法的精确算法，但在模型中没有考虑ASC的载荷量约束，并且子问题的求解依赖于主问题的对偶变量，每次迭代需要重新对子问题建模，影响算法的求解效率。文献[12]提出了ASC车辆路径问题的多目标优化模型，用分支定价算法求解，并与单目标车辆路径问题对比，验证了多目标模型的有效性和灵活性。车辆路径问题的子问题通常是带资源约束的最短路径问题（ESPPRC）。文献[13]提出了K循环消除方法提高对子问题松弛问题下界的约束。文献[14，15]分别提出了标签算法和列生成算法，并应用到车辆路径问题中，标签算法通过迭代过程对标签逐步修正，可以在搜索过程中删除大量标签，提高算法效率，用列生成算法求解了ESPPRC的松弛问题。文献[16]引入了子集-行不等式，极大地改进了分支定价算法中每个节点的下界，但增加了定价问题的复杂性。文献[17]提出了一种基于隐枚举法的精确求解方法，极大地缩小了搜索空间。

在分支定价算法的框架中设计合理的加速策略以提高车辆路径问题中定价子问题的求解效率仍然是目前的研究热点。基于此，本文以最小化ASC总行驶距离为目标，考虑ASC的载荷量以及每个作业点的时间窗和需求量等因素，建立带硬时间窗的ASC车辆路径问题的混合整数规划模型，并改进分支定价算法求解模型，即将脉冲算法嵌入列生成算法提高子问题的求解效率。最后通过求解不同规模的算例验证了模型和算法的有效性，并对影响算法效率的相关因素进行了灵敏度分析。

1 问题描述与数学模型

1.1 问题描述

ASC车辆路径问题可以描述为将集装箱的运输任务分配给ASC，以满足每个作业点（提箱点/卸箱点）的时间窗约束、ASC的载荷量约束和ASC的数量约束。假设前一个任务的卸箱点为后一个任务的提箱点，并以最小化ASC总行驶距离为目标函数，将ASC车辆路径问题建模为带硬时间窗的同时取送货问题（PDPTW）。

为符合PDPTW的数学框架，简化搜索空间结构，首先根据自动化集装箱码头的堆场环境图构建ASC-PDPTW运输网络，用有向图G=（P，A）表示，由作业点集P={0，1，2，...，n，n+1} 和弧集A组成，作业点0和n+1表示车场，n+1为虚拟节点，代表终点，定义节点n到n+1的距离为0，其他n个作业点集记为N={1，2，...，n}。ASC的集合记为V={1，2，...，k}，每个作业点i（i∈N）都有给定的需求量di、所需的作业时间si和时间窗[ai，bi]，ai，bi分别表示该作业的最早开始时间和最晚开始时间，ASC早到必须等待，但不能在最晚作业时间bi之后到达。其中车场的时间窗[a0，b0]=[an+1，bn+1]表示作业完成的周期。ASC的最大载荷量为q，tij表示ASC从作业点i行驶到作业点j(i，j∈N)的行驶时间，cij表示ASC访问运输网络中每个弧段的成本（行驶距离）。

假设q，ai，bi，di，cij均为非负整数，tij，si为正整数。引入两个决策变量x和s，对每个弧段(i，j)和每一辆车k，定义

其中i≠j，i≠n+1，j≠0，sik定义为车辆k在i点开始作业的时间，若k不在i点作业则sik无意义，本文假设a0=0，即对于所有的ASC均有s0k=0。

本文所解决的问题是改进分支定价算法求解ASC最优行驶路径，在各个作业点的时间窗内完成所有的运输任务，并使得ASC总行驶距离最短。

1.2 数学模型

以最小化ASC总行驶距离为目标建立ASC-PDPTW混合整数规划模型。

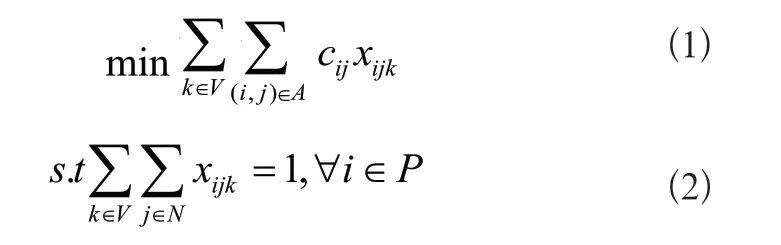
其中约束条件(7)可以线性化为：

Mij是一个很大的常数，可以缩小到max{bi+tij-aj}，{i，j}∈A。

式(1)表示最小化ASC总行驶距离，式(2)保证每个作业点只能被一辆ASC访问且仅访问一次，式(3)表示每辆ASC的载荷量不能超过q，式(4)～式(6)确保每辆ASC由车场出发，依次完成作业后仍回到车场，式(7)表示ASC从作业点i行驶到作业点j的时间约束，式(8)表示ASC到达作业点的时间必须满足时间窗约束，式(9)表示若第k辆ASC从i行驶到j，则xijk=1，否则为0，式(10)给出了ASC数量上限。

2 模型分解

建立的模型中只有赋值约束(2)是车辆耦合约束，其余的约束条件均分别处理各ASC。因此可以将模型化为具有对角结构的线性规划问题，然后用列生成算法求解，从Dantzig-Wolf分解原理出发，将模型分解为带资源约束的最短路径定价子问题和变量数目很大的主问题。

2.1 ASC-PDPTW主问题

设Ω为车辆k(k∈V)的可行路径集合，随着问题规模的增大，可行路径的数目呈现爆炸式增长，因此不能把所有的可行路径都在模型中显性的表示出来。本文从单纯形法的理论出发，将问题转化为求解满足约束的若干条可行路径，并使得目标函数值最小。主问题即为包含这若干条可行路径的集合划分问题。

设Ω为车辆k(k∈V)的可行路径集合，二进制决策变量xkijp=1表示车辆k在它的可行路径集合中的路径p(p∈Ω)中从i到j，否则为0，ykp表示车辆k是否经过路径p，则有：

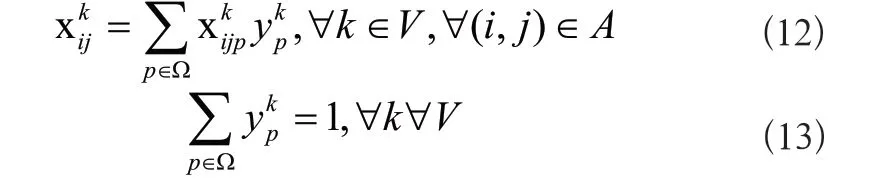
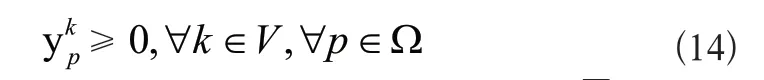
通过xkijp可以定义一条路径的花费为；车辆k访问客户点i的次数为aki，∀k∈V,∀i∈N,∀p∈Ω。

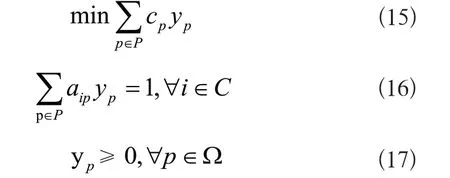
在列生成算法中，并不是所有的列都显性的表达出来，主问题的列集合仅限于已经生成的列，在所有可行路径集合中找到满足条件和目标函数的路径Ω'，称为受限主问题(Restricted Master Problem，RMP)。RMP的模型表示如下：

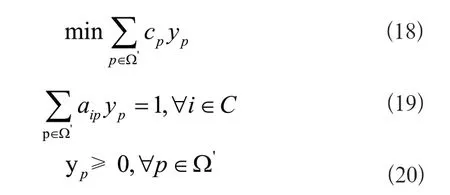
2.2 ASC-ESPPRC定价子问题

ASC车辆路径问题的子问题是带资源约束的最短路径问题（ASC-ESPPRC），是NP难问题。为了找到向RMP可行路径集Ω'中添加的路径，ASC-ESPPRC定价子问题是在考虑约束(3)至(9)的条件下最小化可行路径的节约成本，由原问题分解得到的模型为：

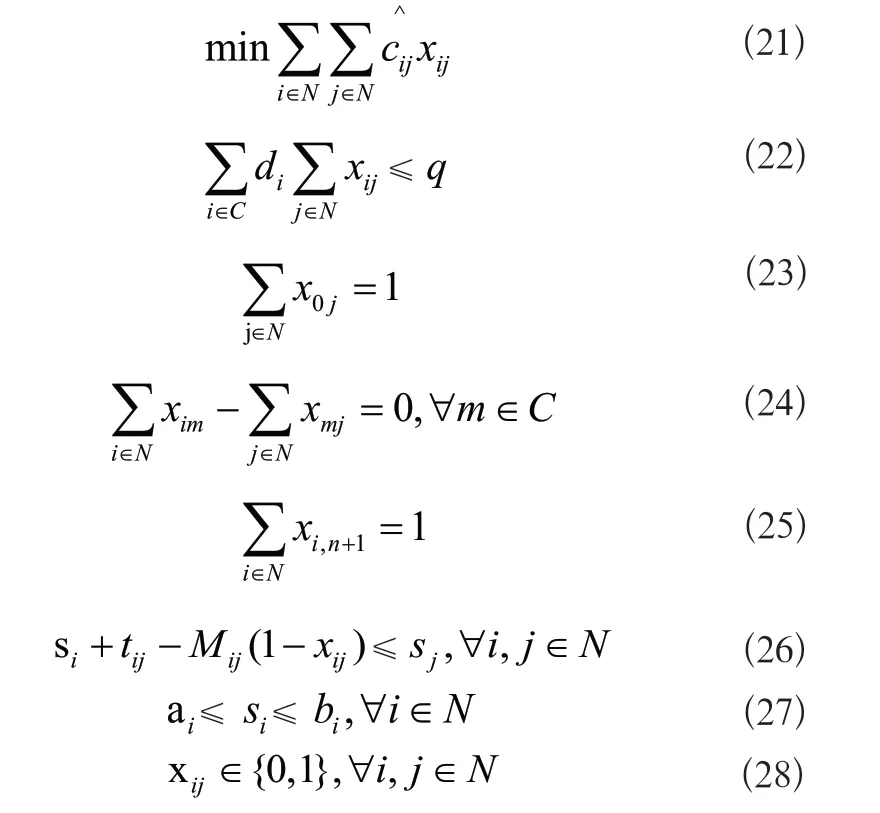
3 改进的分支定价算法

本文从包含部分路径的RMP出发，采用脉冲算法求解ASC-ESPPRC定价子问题，将子问题的解为负的列加入RMP重新求解，如此迭代直到子问题的解为非负则得到了RMP的最优解。将得到的解采用弧分支策略得到最优整数解。图1是改进分支定价算法（Improved branch-andprice algorithm，IBP）的流程图。

图1 IBP算法流程图

3.1 脉冲算法

脉冲算法是通过对已得到的部分路径递归搜索，在扩展过程中部分路径所包含的节点会被不断扩展到最终作业点或剪枝不满约束条件的路径。良好的定界策略能够大大缩小搜索空间，提高算法的求解效率，脉冲算法过程中包含三个不同的剪枝策略。图2为脉冲算法流程图。

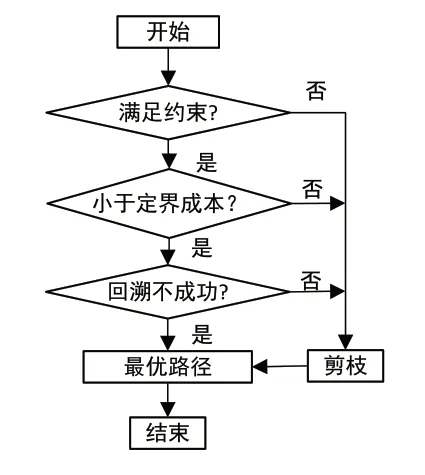
图2 脉冲算法流程图

3.1.1 符号说明

G：访问作业节点（路径）有向图；

ns：脉冲算法的起始节点；

ne：脉冲算法的终止节点；

S：当前节点的路径信息；

S*：获得的最优路径；

r(S)：当前路径节约成本的累加和；

q(S)：当前路径载荷量的累加和；

t(S)：行驶到当前路径花费的时间；

Δ：定界算法中时间变化步长；

[tu，td]：定界过程的时间范围；

ASC每行驶到一个节点，就会运行脉冲算法进行递归搜索。执行上述三个不同的剪枝策略尝试缩小搜索空间，最后到达节点ne的脉冲包含了从ns到ne的所有信息。

3.1.2 脉冲算法流程

针对ASC-ESPPRC定价子问题，求解过程可以分为两个阶段。首先通过定界（Bound）算法计算出到达每个节点的最低成本（cost），该过程称为定界。然后运行脉冲（Pulse）算法进行路径搜索。此时通过定界算法得到的每个节点的最低成本用于剪枝，能够去掉不好的路径。

求解过程如图3所示。a)～d)将当前获得的部分路径S、当前路径节约成本r(S)、当前载荷量累加和q(S)和当前花费的时间t(S)初始化。e)运行定界算法确定ASC行驶到各个节点时的最低成本，如3.2.2所述。f)执行脉冲过程。通过不同的剪枝策略得到最优路径S*，如3.2所述。最后输出最优路径。

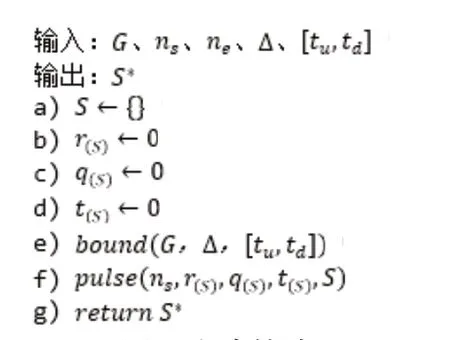
图3 脉冲算法

3.2 脉冲过程剪枝策略

脉冲过程主要包括三个剪枝策略：

If_Feasible：用于检查ASC行驶到当前节点时是否满足约束条件；

Check_Bound：用于检查到达当前节点时的cost是否小于等于通过Bound算法求得的最低cost，若不是则该条路径被剪枝；

Rollback：用于回溯操作，即检查是否有满足三角不等式的节点，使得比原来的路径成本更低，若有则原来的路径被剪枝。

脉冲剪枝策略的执行过程如图4所示，其中Ψ+(ni)表示从当前节点出发后的入度节点。

图4 脉冲剪枝策略

3.2.1 检查约束剪枝策略

当ASC到达当前节点时，首先检查是否满足模型的约束条件，即时间窗约束，载荷量约束以及完成任务的周期约束。运行If_Feasible剪枝策略，当行驶到节点ni时检查是否形成循环、是否超出载荷量q以及是否违反时间窗约束。若其中任何一个不满足，这条路径为不可行路径，将被剪枝。

为检查当前路径是否有循环，本文设置一个标记函数标记在当前路径中已经访问过的节点，若访问过则该部分路径被剪枝。对于载荷量约束，若ASC在行驶到下一节点时载荷量超出，则该部分路径被剪枝。对于时间窗约束，若ASC在bi后到达则该部分路径被剪枝，若在ai前到达则需要等待到ai才可以作开始作业。

3.2.2 定界剪枝策略

定界算法用于求解ASC行驶到不同节点时，在不同最晚到达时间下的最低成本，最终得到ASC在不同时间到达该点的成本矩阵。定义为边界值的上界，随着路径的变化更新，运行定界算法后得到每个节点ni∈N在当前的时间t(S)下的最小节约成本，记为。定界算法的执行过程如图5所示。最低成本矩阵记为，其中为达到最低成本时的时间。

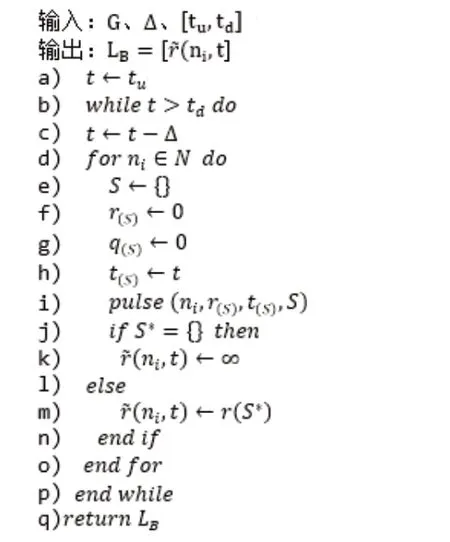
图5 定界策略

tu是访问车场的时间窗上界，Δ是非负的时间步长，访问节点的最晚到达时间从tM开始每次减少一个时间步长，直到减小到td。即当访问节点ni时，首先设置到达该节点的最晚到达时间为t(S)=tM-Δ，求得的最优解为当前最小节约成本的下界。若此时t(S)≠td，则继续设置该节点的最晚到达时间为t(S)=tu-Δ，计算最优解。此后的过程重复上述操作，直到当前访问节点的t(S)=td。此时得到不同节点在不同最晚到达时间下的最小成本矩阵。

3.2.3 回溯剪枝策略

由于脉冲算法是通过递归的方式寻找路径，因此采用深度优先搜索寻找路径节点。深度优先搜索的缺点是选择了分支定界树上的分支后必须遍历完，但不一定得到最优解，此时需要返回重新搜索。本文采用回溯策略，在获得部分路径的最后一个节点就执行回溯操作，寻找是否有更优的路径，若有则替换当前最优部分路径。如图6所示，假设有部分路径Ssi从节点ns出发到达ni，然后访问节点nl，最终到达nk。回溯剪枝策略会在重新判断到达终点前选择的节点，S'SK为回溯操作后可选择的另一条路径，由Ssi直接扩展到节点ni，不经过nl直接到达nk。此时需要进一步判断路径S'SK是否满足以下约束：1)S'SK⊆SSK；2)t(S'SK)≤t(SSK)；3)r(S'SK)≤r(SSK)；4)q(S'SK)≤t(SSK)。

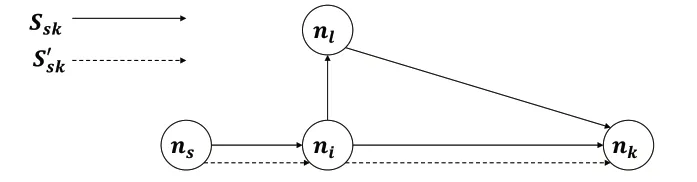
图6 回溯剪枝策略示意图

由上述分析易知，约束1)，4)显然满足，因此只需要判断约束2)，3)是否满足。若满足则用S'SK替换SSK，即原路径被剪枝。

3.3 列生成算法与整数解

由列生成求解得到的RMP的最优解可以是整数或浮点数，若为整数则与当前上界相比较，小于当前上界则更新上界值并剪枝。对于浮点数解，若小于当前上界则在求得的变量中选择最接近0.5的变量进行分支，得到两条路径S1和S2，S1中包括弧段(i，j)，S2不经过i点到达j，删除当前节点同时将分支节点加入分支定界搜索树。若大于当前上界则不需要分支。

4 实验结果分析

本实验使用Eclipse JDK 4.3.0版本，在Java多线程中调用Cplex求解模型，实现了本文IBP算法。进行实验的计算机参数为Inter(R) Core(TM)i5-8250U CPU @ 1.60GHz 1.80GHz。

实验首先在Solomon标准测试集中选取5组小规模算例，分别用分支定界算法和IBP算法求解，并用本文IBP算法求解得到了部分较大规模Gehring&Homberger算例的最优解，同时对影响算法效率的相关因素进行灵敏度分析。

4.1 对比实验及小规模算例测试结果

在Eclipse中编写分支定界算法，调用Cplex求解小规模算例，并与改进的分支定价算法求解结果对比。从Solomon标准测试集中选取5组小规模算例进行测试，测试结果如表1所示。图7为相同规模下传统分支定界算法与IBP算法求解时间的对比。

表1 分支定界算法IBP算法小规模算例结果对比

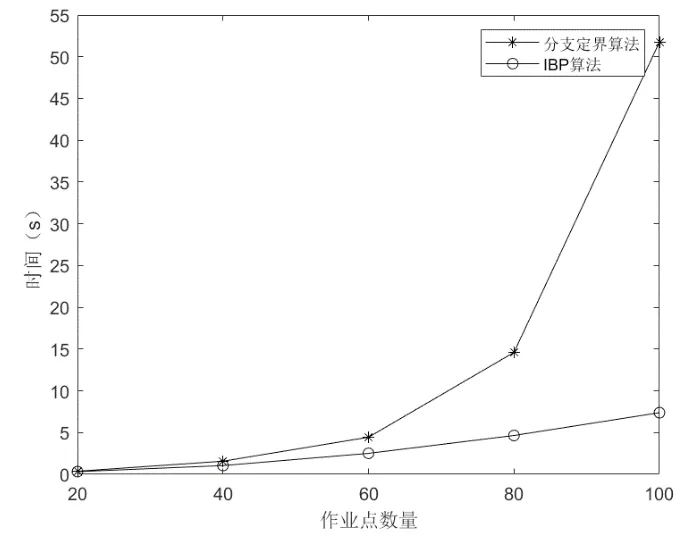
图7 分支定界算法与IBP算法效率对比

通过表1可以看出两个算法求解的ASC行驶总距离基本吻合，平均误差小于1，且IBP算法求解时间比分支定界算法平均值短11.37s。通过图7更可直观看出，随着问题复杂程度的上升，IBP算法效率高于分支定界算法。

选取不同类型的算例测试算法的有效性。C类算例表示作业点集中在部分区域，R类算例表示作业点随机分布，RC类算例表示作业点既有集中分布、也有随机分布的。表2为改进的分支定价算法在不同测试集下的计算结果。表3列出了三类算例的部分ASC车辆行驶路径。

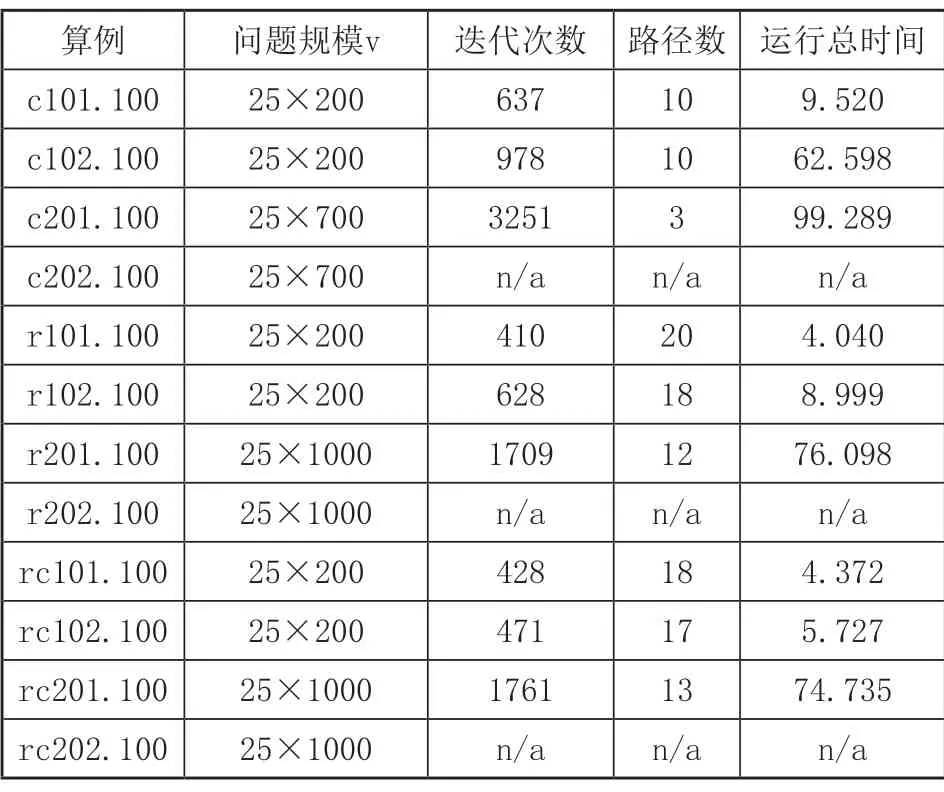
表2 改进的分支定价算法求解结果

表3 IBP算法求解部分算例路径

由表2、表3可得，随着问题规模的增加，迭代次数不断增加，即子问题求解次数增加。求解时间R类＜RC类＜C类，即作业点越分散计算时间越短。作业点数量相同条件下，随机分布的R类算例，路径数比C类算例和RC类算例多，每条路径中访问的作业点数量少，需要的ASC数量多，C类算例中每条路径的作业点数目分配较均匀，所需的ASC数量较少。即作业点越分散求解时间越短，但所需ASC数量越多。

4.2 较大规模算例求解结果

在Gehring&Homberger数据集中选取了7组较大规模的C类算例求解，作业点规模为200、400、600，设置可接受的最大求解时间为2小时，定界策略中的时间步长。实验结果如表4所示。

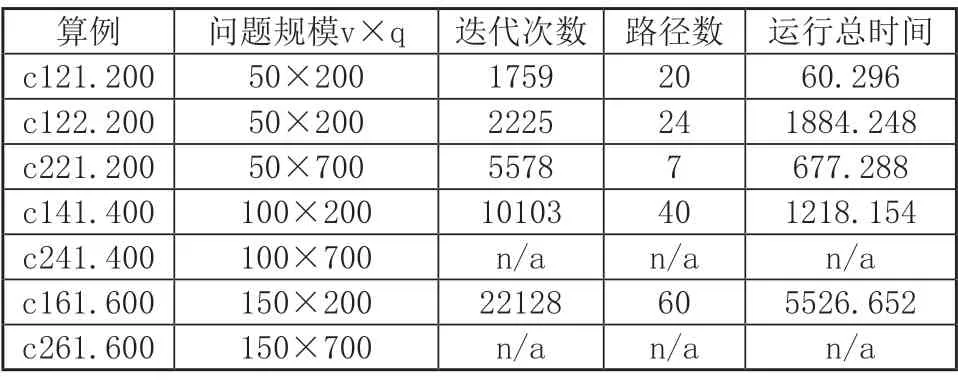
表4 较大规模算例求解结果

由表4可得，IBP算法能够用于求解一些较大规模的ASC车辆路径问题，并且能在不同规模算例和可接受的时间范围内求得最优解。问题规模与求解时间成正比，但得到的可行路径数目与求解时间不一定成正比，这与算例本身的数据复杂程度有关。可行路径少的算例中每条路径的作业点较多，ASC的利用率较低；可行路径多的算例中ASC利用率较高。

4.3 灵敏度分析

在IBP算法中，子问题求解过程中定界策略对求解效率起关键作用，另外ASC的载荷量也会直接影响求解结果。因此分析定界策略中不同时间步长与不同ASC载荷量对算法求解效率的影响。为保证实验的一般性，从Solomon标准测试集中选取6组作业点规模相同的算例进行实验。分别分析定界策略中不同的时间步长和ASC不同载荷量对算法求解效率的影响。

1）定界策略的时间步长

为研究不同时间步长下的定界策略对算法的效率影响，在其他参数不变的条件下，每组算例依次设置步长为4、8、12、16、20进行测试。实验结果如表5所示。

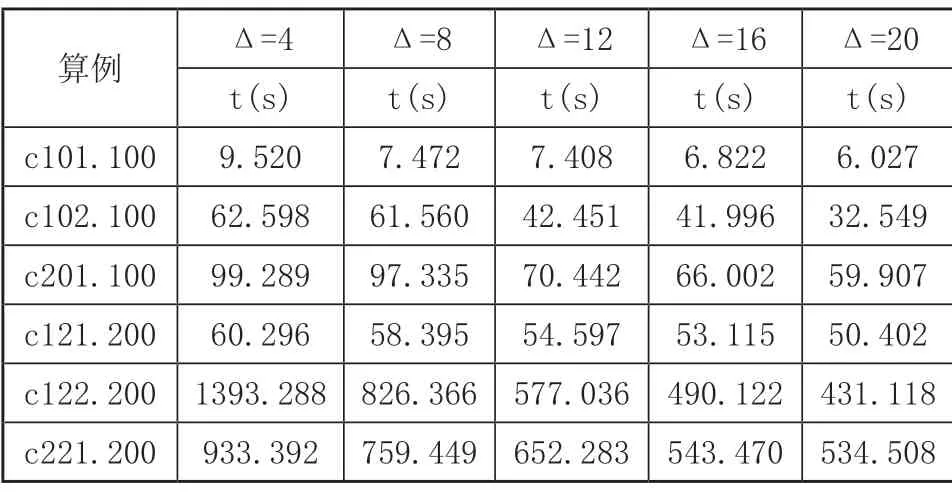
表5 不同时间步长灵敏度分析

由表5纵向来看，随着算例规模的增加和问题本身复杂程度的上升，算法的求解时间不断增加，但都能够在0.5小时内得到最优解；横向来看，上述6个算例从Δ=4增加到Δ=20，算法求解时间逐渐减少，求解效率分别提升了36%、48%、40%、16.4%、69%和42.7%。验证了时间步长对算法效率的影响，时间步长越大得到的成本矩阵规模越小，求解时间越短。

2）ASC不同的载荷量

为研究ASC在不同载荷量下对实验结果的影响，选取6组算例进行测试，在其他参数不变的情况下，设置可接受的求解时间为2小时以内，分别设置ASC载荷量为200、400、600、800和1000进行测试。实验结果如表6所示。

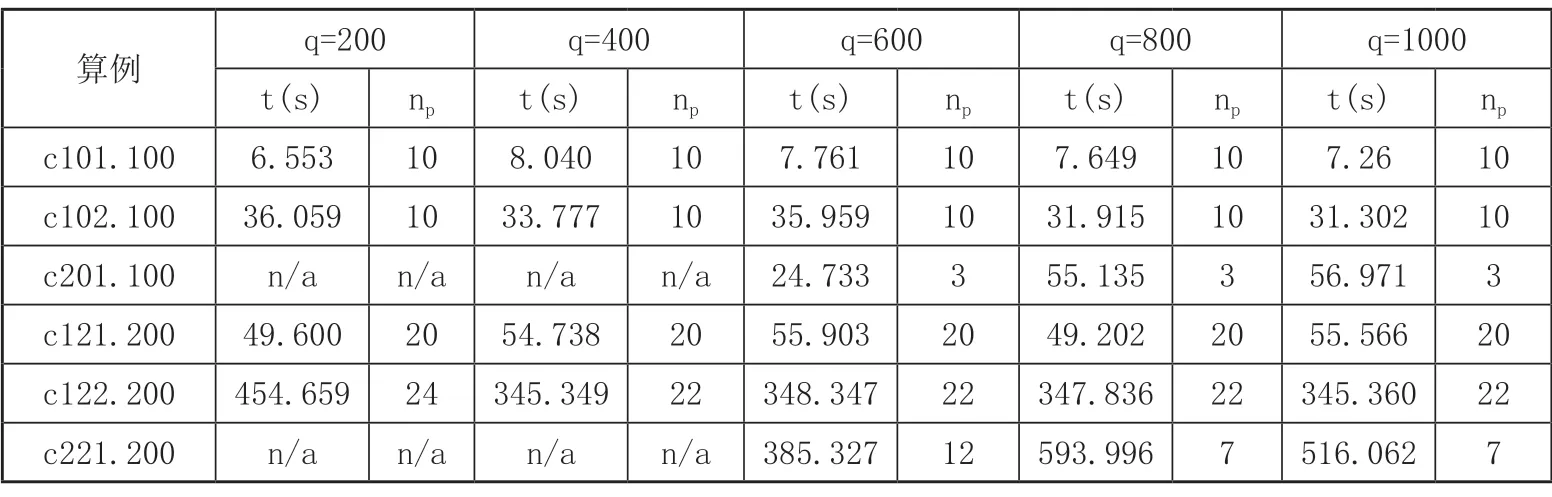
表6 ASC不同载荷量灵敏度分析

由表6 可得，对于数据简单的小规模算例，如c101.100和c102.100，不同载荷量下得到的最优路径相同，随着ASC载荷量的增加，求解时间呈减少趋势，最大差值为1.487s和4.757s，ASC不同载荷量对求解时间的影响小于5s。对于数据较复杂的算例，如c201.100和c221.200，q＜600时无法在可接受时间范围内得到最优解，q≥600时能得到最优解，在q=600时求解时间最短，此后得到的路径数趋于稳定，即随着ASC载荷量的增大，最优解趋于稳定。对于较大规模算例，如c121.200和c221.200，c121.200在不同载荷量下得到最优解的时间差值小于6s，c122.200由q=400增加到q=600时得到最优解，随着q的增加求解时间基本稳定。由上述分析可得，ASC载荷量越大算法的求解效率越高，对于数据简单的算例对求解时间的影响小于7s，对于数据复杂的算例，ASC达到一定的载荷量后得到的最优路径趋于稳定。验证了ASC不同载荷量对算法效率的影响，且不同的算例能够求得最优的ASC载荷量。

5 结语

本文建立了自动化集装箱码头ASC-PDPTW混合整数规划模型，提出了一种求解ASC车辆路径问题改进的分支定价算法。用脉冲算法求解定价子问题并嵌入分支定价算法框架中，定界过程中包含三种剪枝策略，用于有效缩小解搜索空间，提高求解效率。设计了小规模算例的对比实验；求解并分析了较大规模算例的实验结果，并进一步对不同的时间步长和ASC载荷量进行灵敏度分析。作业点在20至100内小规模算例的求解时间比传统分支定界算法平均提高11.37s；作业点在200至600的较大规模算例能够在可接受时间范围内求得最优解，即该算法不仅能够更加快速的求解小规模算例，也能够在可接受时间范围内求解一些较大规模算例。在灵敏度分析中，随着定界策略中时间步长增加到20，求解效率平均提高42.01%；随着ASC载荷量的增加，对于数据简单的算例得到的最优解基本稳定，对于数据复杂的算例，载荷量越大求解效率越高，在达到最优载荷量后最优路径不再变化，求解时间会增加。实验结果验证了本文所建立模型的可行性，提出的IBP算法能够有效提高求解ASC最优行驶路径的效率。