电力输配电线路运行短路故障自动检测方法研究

王德海，傅洪全，陈 曦，黄泽华

（国网江苏省电力有限公司技能培训中心，苏州 310015）

0 引言

经济飞速发展离不开电力支持，同时较大的电力需求促进了经济快速发展，可见电能的质量变得越来越重要。输配电作为给用户直接提供电能的环节，以串联电容的方式补偿电抗，优化输配电线路的工作稳定性[1]。但随着城市化进程发展加快，越来越多的建筑、行业以及其他用户，对于电能的需求越来越大，为了实现“覆盖式”供电、合理调度用电，现阶段的电力输配电线路结构变得越来越复杂，包含的支路逐渐增多，产生了大量故障问题，其中短路故障最为明显，大约有10种故障类型。此种情况下的输配电网运行，需要利用故障检测方法，排查短路故障问题，但目前的检测方法对于故障类型的分析较为单一，导致检测存在极大误差，给实际维修工作带来困难的同时，也耗费了宝贵的维修时间，针对这一问题研究全新的电力输配电线路运行短路故障自动检测方法。

1 电力输配电线路运行短路故障自动检测方法

1.1 构建短路故障仿真模型

电力输配电线路长时间暴露在自然环境当中，受外力破坏、气体腐蚀以及恶劣气候影响，存在运行短路故障问题，包括单相短路、两相短路、三相短路，细分上述短路总共有10种短路故障类型，为了自动检测短路故障得到可靠的检测结果，构建电力输配电线路运行短路故障仿真模型。已知电阻、电抗以及电导等参数沿线均匀分布，所以构建模型时难度较大，为此不考虑线路分布参数的自身特点，面对短距离检测时，可建立一个“П”型线路模型。该模型中的分布参数包括输配电线路总电阻R、电感G、各相导线之间、导线与大地之间的电容D，通过下列公式计算获得：

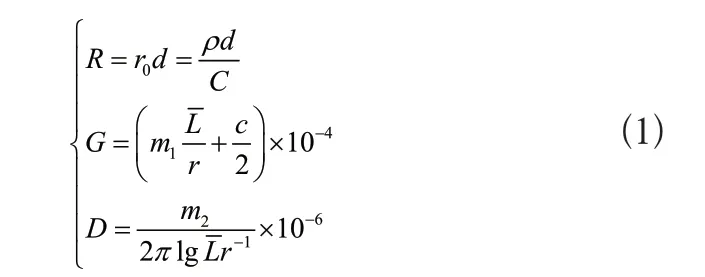
式中：r0、r表示导线电阻的单位长度和半径；d表示导线长度；p、c表示材料的电阻率和导磁系数；C表示导线截面积；m1、m2表示常数项；表示三相导线之间的平均距离[2]。当电力输配电线路的运行距离较远时，模型的测量精度有所下降，所以根据线路的分布特性，以串联多个短距离线路模型的方式，模拟长距离线路中的分布参数特征，近似得到一个能够获取长距离线路分布参数的故障仿真模型，如图1所示。

图1 长距离条件下的仿真模型

上述参数解释对应图1中的参数。已知输配电线路短路电流大小与故障类型相关，且短路电流大小与电源特性及输电线路参数也存在一定联系，所以利用MATLAB建立上述两种短路故障仿真模型，得到单相短路、两相短路、三相短路的电流，公式为：

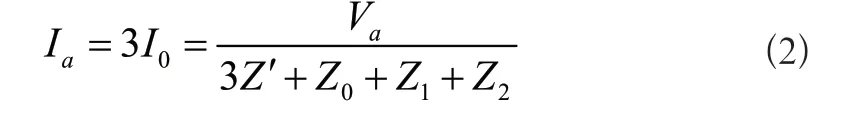
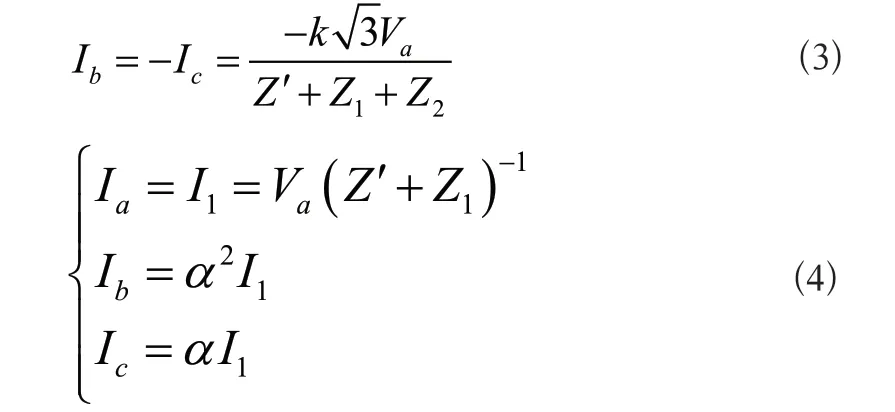
式中：Ia、Ib、Ic表示a相、b相、c相短路电流；I0、I1表示零序电流和正序电流；Va表示a相发生故障时的相电压值；k表示衔接点数量；Z'表示故障点处的过渡电阻；Z0、Z1、Z2表示零序阻抗和两个线路完全不同的正序阻抗；a表示复数算子。根据短路故障仿真模型显示短路故障数据，进一步分析短路信号在电力输配电线路上的所在位置。

1.2 定位发生短路时的故障电流信号

根据故障仿真模型反馈的短路电流，定位故障电流信号。已知发生短路后，母线端测量装置不仅接收故障行波，还会接收折射行波和反射行波，这些波幅具有多样性和复杂性特征，检测装置根据这些波幅无法准确获得故障来源，所以根据故障仿真模型反馈的信息，通过假设故障点判断行波与检测装置之间的时差，确定第一反射波与检测装置之间的时间区段。假设时间为t，最早与最晚条件下存在t∈（tmin，tmax）。假设故障发生在母线附近的点A处和末端的点B处，在点A和点B两个位置，该点和母线之间的第一反射波，只往返传输了一次，且第一反射波还在两个节点之间传输了三次，则最短和最长时间为：

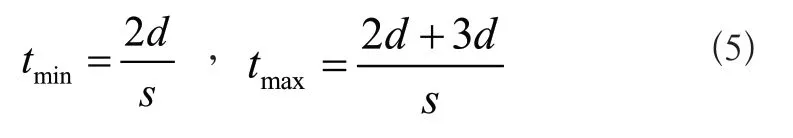
式中：S表示行波传播速度。出现波阻抗不连续的现象时，暂态行波的多次折射与反射导致波头信息相互叠加产生误差，所以采用VMD算法处理模态混叠问题[3]。假设模态分量共有n个，通过Hilbert变换模态分量得到信号函数，然后将预估的n个模态分量的中心频率和带宽频谱，调整到特定频带当中，通过约束带宽控制暂态信号，该算法的计算过程为：

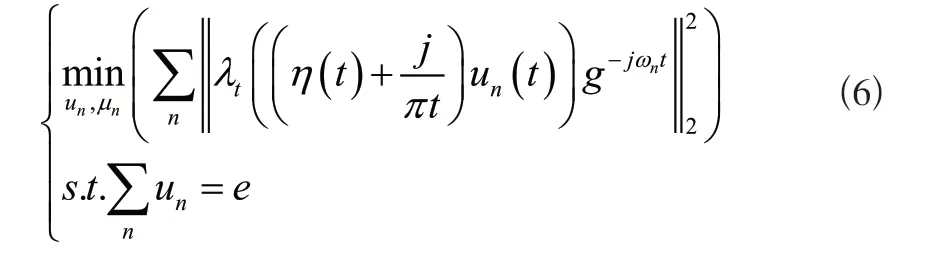
1.3 提取短路故障特征

针对不同故障类型提取多组不同短路故障特征，但由于VMD算法无法表征多尺度下的故障信号特征，所以在本环节中，利用多尺度熵弥补VMD算法的不足，提取故障信号的不同尺度特征，最大限度挖掘发生短路故障时所包含的故障特征，从而获得故障检测所需的特征向量。多尺度熵的参数包括嵌入维数m、尺度因子β、相似容忍度f，计算时间序列尺度因子的长度均值，生成不同时间序列，根据多个序列得到多尺度熵。多尺度熵融合下，设置离散原始时间序列为{h1，h2…，hn}，利用尺度因子β粗粒化处理该序列，得到：

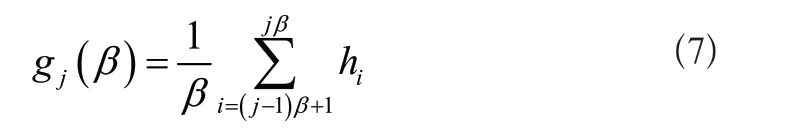
式中：j表示离散时间序列长度。假设嵌入维数和相似容忍度限值已知，则随机两个节点i和节点j之间的距离为：

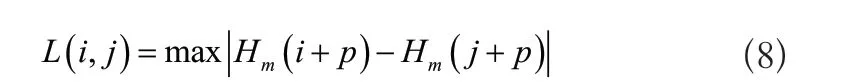
公式中：Hm(i+p)、Hm(j+p)表示变化幅度为p时的向量值[4]。将上述结果与距离总数进行比较，并计算平均值，得到：

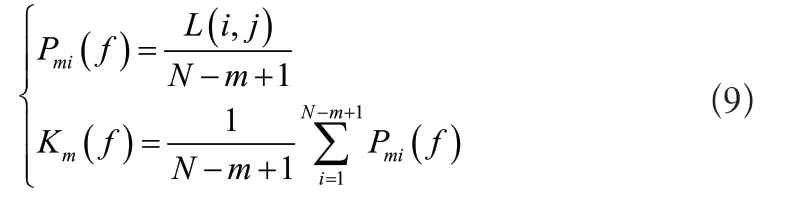
式中：N表示m维时间序列向量总数；Pmi(f)表示向量比值。重复上述计算，当N有限值时得到样本估计熵的计算结果：

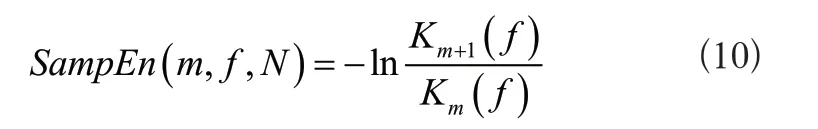
然后再次重复上述四步计算，得到多尺度熵的值，也就是式(10)的多个计算结果，根据该结果区分故障特征，在应用VMD算法定位故障电流信号位置的前提下，融合多尺度熵提取短路故障特征。

1.4 基于参数估计自动检测短路故障

将特征提取结果作为已知条件，采用参数估计的方式自动检测短路故障距离。假设短路故障发生在i-j分支当中，则故障点到终端的传输方程，可通过下列公式描述：

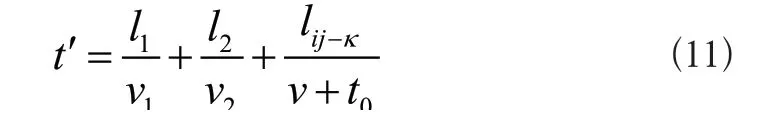
式中：t'表示测量获得的行波到达时间；l1、l2表示故障点到架空线和电缆的距离；v、v1、v2表示行波波速；lij-k表示存在k故障的线路；t0表示运行过程中，短路故障的发生时刻。考虑到检测对象为电力输配电线路运行短路故障，所以考虑弧垂效应，在式(11)中加入弧垂系数γ，该参数的计算公式为：

将线路上的短路故障点检测，转换为地面距离上的短路故障点检测，消除弧垂效应对检测结果的影响。根据式(11)和式(12)计算得到多组传输方程，联立得到n个检测点的矩阵形式：

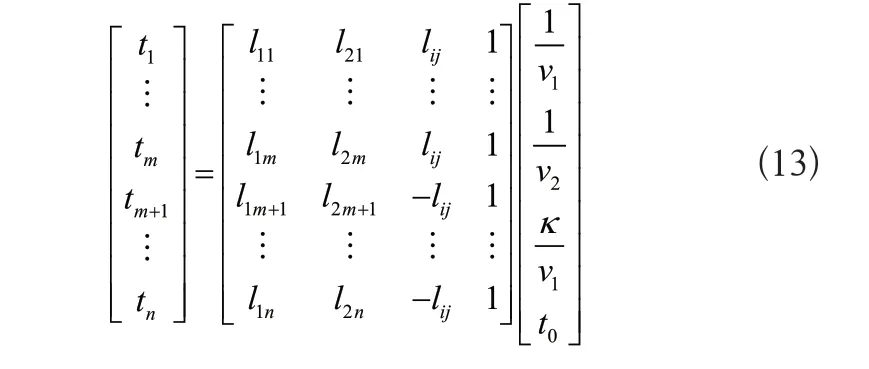
简化上述公式得到t=SampEn（m，f，N）Ex，其中t表示时刻列向量；E表示系数矩阵；x表示为自变量，是波速、长度、时间等参数构成的向量集合。但实际工作中存在干扰因素，所以检测结果还是存在一些偏差，因此基于参数估计修正偏差，将简化后的公式再次修正，得到：

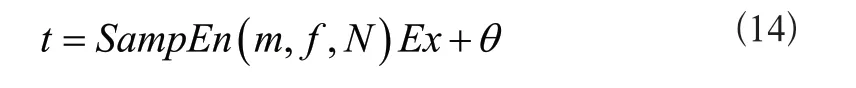
式中：θ表示误差向量[5]。根据上述公式可知t值，待求解向量为x，当θ=0时，式(14)存在无穷解；当θ为任意值时，需要建立误差最小的目标函数，得到：

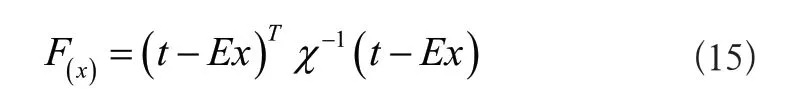
公式中：x表示为测量误差方差矩阵。求导上述公式并要求求导结果为0，即，根据上述计算求解最佳估计值x，利用该值设置电力输配电线路运行短路故障自动检测中，测点在配置区间中的所在位置。自动检测方法根据参数估计值，判断故障点在电力输配电线路中的所在位置，根据不同的时间差矩阵，判断结果生成差分矩阵：

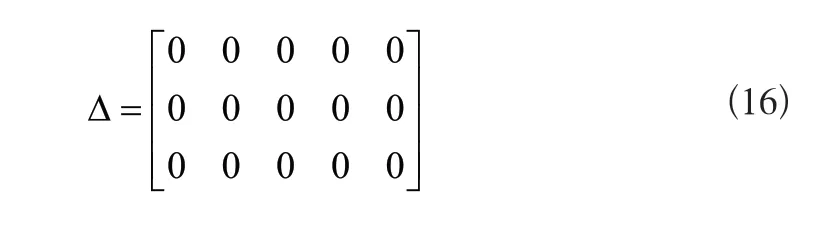
式中，第1列至第5列分别表示5条不同的检测线路。当公式中出现大于0的数据时，说明检测过程中发现故障，若中间的值为0，两端显示其他大于0的数据，说明该线路的前半段和后半段区间均存在短路故障，根据上述公式得到检测结果，至此实现对电力输配电线路运行短路故障的自动检测。

2 应用测试

2.1 测试环境准备

针对研究的检测方法搭建实验测试环境，选择监测终端、智能集中器和后台主站。选择的监测终端适用于110kV～500kV电压等级的输配电线路，当输配电线路运行正常时，可以定时上传输配电线路的感应电流，通过建立的故障仿真模型分析电流状态。当发生不同类型的短路故障时，监测终端通过闪光警示功能和射频通信功能，为智能集中器提供关键数据。智能集中器被安装在电力杆塔上，接收监测终端发送的实时数据后进行转发，上传到主站。此次实验要求选择的集中器需，要具备遥测功能和遥信功能，其中前者用来用来传送电流信息，后者用来采集带电状态。无论线路是否出现短路故障，集中器都能将信息发送给主站，反馈输配电线路的实时运行情况。后台主站是一台工业控制计算机，接收智能集中器的上传数据，通过组态显示和故障统计分析，实现自动检测。综合来说，利用监测终端获取线路电流；利用集中器接收与上传电流数据；利用主站接收数据、分析输配电线路运行状态。图2为测试硬件组图。

图2 测试硬件

根据上述测试环境，在高、中、低三种导线电流的测试条件下，对上述硬件装置进行参数校正，尽量让测试结果的误差最小，让检测数据贴近实际数据。测试过程中调节加压器，观察输配电线路上的电流监测值，利用钳形电流计读数，然后根据智能集中器上传的数据，最后后台主站进行电流分析，图3为钳形电流计和主站界面的测试结果。

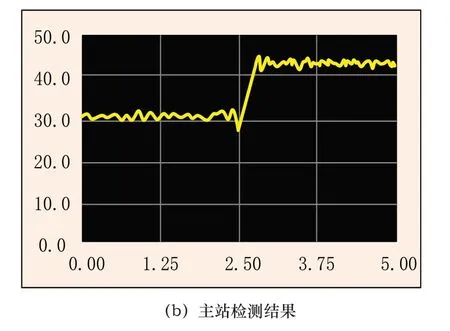
图3 硬件装置测试

图3(b)中横、纵坐标分别代表时间s和电流A。对比图3显示的测试结果可知，钳形电流计测量的实际电流为48.97A，主站根据电流检测曲线得到的短路电流为48.45A，虽然存在约0.5A的检测误差，但已经达到了一个较好的效果。将设备安装到实际输配电线路当中，应用此次研究的检测方法，自动检测电力输配电线路运行短路故障。

2.2 自动检测短路故障

根据搭建的硬件测试环境，应用此次研究的自动检测方法，检测电力输配电线路运行短路故障线路，利用建立的短路故障仿真模型生成仿真图，如图4所示。

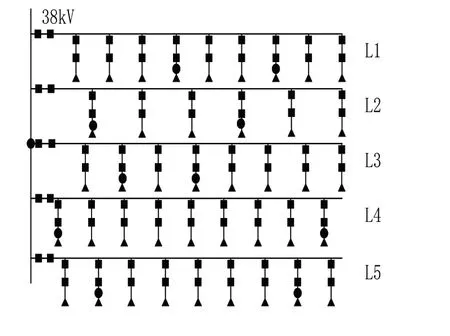
图4 仿真模型

图中的线路长度单位为km，L1、L2、L3、L4以及L5表示输配电线路编号，线条表示架空线，方块表示电缆线，圆形表示行波测点，三角表示发电机组。为了保证测试结果的真实性，检测方法在5条线路中分别设置了不同位置的2个测点，最后在38kV处再设置一个测点，合计设置了11个测点。测试从两个角度，验证本文自动检测方法的可行性：

1）故障位置；

2）检测行波测点附近的短路故障区间。

仿真线路L1发生短路故障，故障位置与电缆端之间的距离为7.5km，发生故障的时刻为0.05s，表1为11个测点行波波头的到达时刻。

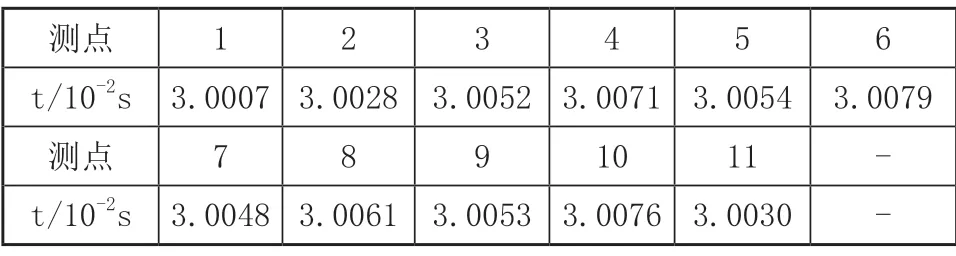
表1 测点行波测量信息

通过参数估计的方式，得到无短路故障时的时间差矩阵△t、11个测点在实际测量条件下的时间差矩阵△t'，公式为：

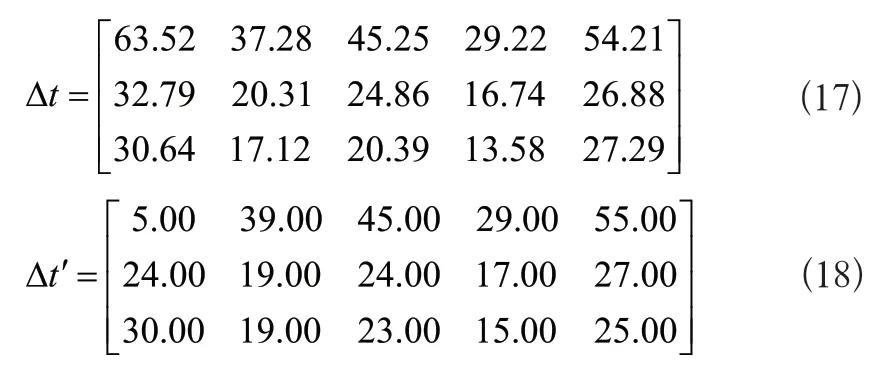
根据公式（16-18）得到差分矩阵：

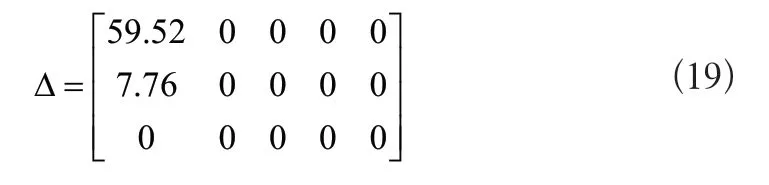
根据公式的第一列可以确定，线路L1存在故障，且故障发生在线路L1的前半段。采用本文方法检测短路故障，为了进一步说明本文方法的应用效果，将目前基于功率因数法的故障检测方法，也应用到同一测试中，并将结果一同绘制在图5中。

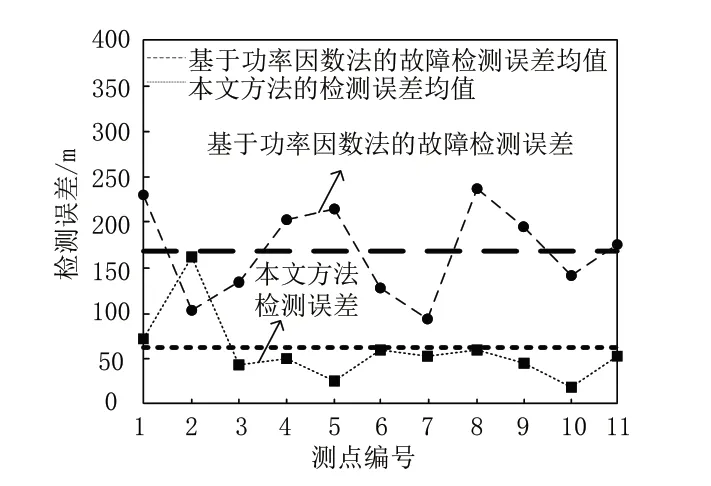
图5 短路故障检测误差

根据图5显示的测试结果可知，本文方法在个别位置上的检测误差，高于基于功率因数法的故障检测方法，但所有测点的检测结果，大部分小于误差均值。计算两种方法的平均误差，分别为170.2m和69.8m，说明本文方法有更好的检测精度。

3 结语

此次研究的检测方法，利用新的仿真模型细化了不同类型的短路故障，为特征提取工作提供了可靠的前提条件。但综合整体设计来看，新的检测方法计算步骤和涉及的参数较多、设计方法较为复杂，在实际工作过程中增加了难度，今后可以简化部分计算步骤，或优化仿真模型，减少由于计算可能带来的问题。