柔性关节机器人参数分步辨识策略研究

陈飞翔，李成刚，储亚东，王剑，岳云双

(南京航空航天大学 机电学院，江苏 南京 210016)

0 引言

机器人动态控制需确定动力学参数，再通过设计激励轨迹，将采样点数据代入动力学模型，并结合相关辨识方法以求解参数值并验证。柳贺等将机器人动力学模型线性化处理后，使用多项式作为激励轨迹，并用最小二乘法辨识参数[1]。ATKESON C G等依据辨识矩阵上三角结构，将参数分成两组进行辨识[2]。丁亚东等鉴于机器人肘、腕关节差异性，将六自由度机器人前后三关节参数分开辨识[3]。分步辨识利于简化模型，但上述研究从机器人具体结构或辨识矩阵特殊形式说明参数集可分成独立的参数组，进而进行分步辨识，故其不具普适性。

张铁等提出先完成摩擦参数辨识，使动力学模型可线性化，再辨识惯性参数[4]。GROTJAHN M等根据不同激励条件，选择对应关节组合运动，实现分步辨识[5]。对于无法独立分离的参数，只可将已辨识参数代入后续辨识方程组中，则此时会产生误差累积。但各研究均未给出减少误差的具体方法。

本文针对柔性关节机器人，首先建立了包含重力补偿的动力学模型，同时将模型线性化处理。随后，依据各参数的独立性进行初分组，并确定对应激励轨迹形式，将辨识矩阵转换为观测矩阵，分析其秩与条件数，进行再分组。最后，结合变量间的关联关系确定辨识顺序，采用最小二乘法进行参数分步辨识。以二自由度机器人为例，通过本文所提出策略，得出具体的参数分组与辨识顺序，并验证了策略可实现模型所有参数的辨识。

1 机器人动力学模型

将柔性关节简化为图1所示模型，即用刚度为ki的弹簧表示谐波减速器中柔轮的柔性，θmi为电机i转子输出转角，θri为减速后转角，θli为最终连杆i输出转角。

图1 柔性关节机器人关节简化模型图

由于谐波减速器采用行星齿轮传动，故输入与输出轴轴线可视作重合，又因质量主要集中在连杆，速度集中在转子，故仅考虑转子与连杆动能。由此，可用标准D-H法建立连杆与转子坐标系。

以二自由度机器人为例，建立如图2所示的坐标系。设O′i-x′iy′iz′i为转子坐标系，Oi-xiyizi为连杆坐标系，li、d′i分别为杆长与电机安装位置几何参数。

图2 二自由度柔性关节机器人坐标系分析图

由D-H参数可得各系变换矩阵，后利用拉格朗日方程建立机器人动力学模型。因转子上任一点的速度由自身相对转速与对应杆牵连速度组成，使得转子动能中存在转子转角与连杆转角耦合项。当减速器减速比较大时，可忽略连杆转速。另设转子质心位于旋转轴上，由此可消去耦合项，同时简化重力势能项，利于后续参数辨识。最终柔性关节机器人动力学模型如下所示：

(2)

τ=K(N-1θm-θl)

(3)

本文针对装有转矩传感器的机器人进行重力补偿。目前机器人模型中，重力补偿多是针对六维力传感器，抑或是研究并联机器人，此处给出柔性关节串联机器人的重力补偿模型。图3为机器人在静止状态下关节所受重力矩作用示意图。

图3 机器人静态下的关节受力分析图

因关节2跟随连杆1运动，连杆1与转子1重力未对关节2产生相对运动趋势，所以关节2转矩传感器仅受到连杆2的重力作用。可求得如下关系式：

(4)

(5)

取Mg1、Mg2的Z维度数值，即得作用在关节1、关节2轴上的总重力矩Mg1Z、Mg2Z。机器人运动状态下，转矩传感器示数包括零点值、重力矩、外力矩与连杆惯性力，有

τ=MgZ+M0+τext+Fa

(6)

式中：MgZ为重力矩向量；M0为传感器零点向量；Fa为连杆惯性力。联立式(1)、式(6)，可得式(7)，即为基于转矩传感器的机器人重力补偿动力学模型。

(7)

其中g′v为gv与MgZ之差，两者具有相同参数，故可合并。

2 参数辨识策略

分析机器人动、势能公式，可知动力学方程可化作关于惯性参数的线性方程，且当摩擦、阻尼等均采用线性模型时，机器人整体动力学模型可线性化。此处考虑关节柔性与重力矩，其对应模型在形式上同样易化为线性方程组。

采用最小二乘法求解线性方程组的解，则此时需保证系数矩阵非奇异，故去除模型中的线性相关项，使所对应参数化作最小参数集，对应系数矩阵行、列满秩。可得如下方程组：

Y[pg,pI,plf]T=τext+τ

(8)

Ym[pm,pmf]T=τm-N-1τ

(9)

(10)

MgZ+M0=[Yg,E][pg,M0]T

(11)

式中：pg为重力矩相关参数；pI为惯量相关参数；plf、pmf为连杆、转子摩擦参数；pm为电机相关参数；pk为弹簧刚度参数；Y、Ym、Yk、Yg为各方程组系数矩阵；E为单位矩阵；n1、n2为对应关节减速比。

设计激励轨迹θl=θl(t)或θm=θm(t)，t为轨迹运行时间。依据设备确定采样频率fs，以式(8)为例，可将方程写作如下形式：

[τext0+τ0,τext1+τ1,…,τextNA+τNA]T=

YN[pg,pI,plf]T

(12)

其中：T为单次运动时间；YN为辨识矩阵Y的观测矩阵；NA=Tfs为时间T内除0时刻外的总采样点数。当确定激励轨迹后，控制机器人运动，代入实验所测反馈值，得YNr，则可由最小二乘法得出所求参数值。

由此可知，YN中线性无关行向量必须大于等于所求变量数。故在进行辨识实验前，需验证YN的秩。本文采用不同变量表示不同时刻采样值，变量间彼此独立，则此时系数矩阵无需按采样频率进行扩充，仅需满足行数大于等于对应变量数。如pm为六维向量，而Ym行数为2，则仅需取3组无关变量作为3个时刻的采样值，求解该伪观测矩阵的秩即可。

当机器人静止，且无外力矩作用时，若(Yg,E)满足秩要求，则式(11)可进行辨识。但计算知(Yg,E)不可能满秩，故无法单独进行重力与零点的参数辨识。同理，式(8)在无摩擦力的情况下才可辨识。

经对各式系数矩阵秩的分析，可确定各参数的基本辨识顺序，即必须先单独进行摩擦参数pf辨识，后代入连杆模型，以辨识pg与pI，进而求取M0。因系数矩阵满秩，故pm、pmf可直接辨识，而式(10)同时包含连杆与转子转角，可直接沿用前连杆或转子所得激励轨迹进行辨识。

3 优化参数辨识策略

cond2(A1A2)≤cond2(A1)cond2(A2)

(13)

其中：cond2(A1A2)一般接近其最大值；A1、A2为任意矩阵。当式(10)与式(9)联立时，有：

[Ym,N-1Yk][pm,pmf,pk]T=

[Ym,E2×2]diag(E6×6,N-1Yk)[pm,pmf,pk]T=

(14)

[τm0,τm1,…,τmNA]T

(15)

(16)

综上所述，对于机器人动力学模型参数辨识，需要从系数矩阵的秩与条件数两个方面出发，确定各参数组合情况。所提参数分步辨识策略流程如图4所示。

图4 机器人动力学模型参数分步辨识策略

当考虑阻尼、干扰力矩，或是分析刚性机器人等，上述策略仍适用。对于二自由度柔性关节机器人，具体辨识过程如图5所示。

图5 柔性关节机器人参数分步辨识流程图

由于使用最小二乘法后，对应系数矩阵条件数为观测矩阵条件数的平方，故为保证精度，观测矩阵条件数一般<10。

4 策略验证

针对二自由度柔性关节机器人，采用多项式形式的激励轨迹，以验证所提策略的可行性。为防止偶然性，将多项式轨迹修正为周期函数，有

θ(t)=a0+a1mod(t,T)+a2[mod(t,T)]2+…+

aNF[mod(t,T)]NF

(17)

式中：θ为任意关节连杆或电机转角；ai为激励轨迹系数；NF为多项式次数；t为时间参数；T为运动周期；mod(t,T)为t对T作取余运算。为保护设备，应使电机柔性启动，且在安全范围内运动，有边界条件如下：

(18)

依据条件方程数目，可知NF≥8。此处采用八次多项式作为激励轨迹，代入各方程的观测矩阵中。同时，为简化运算，统一指定初始角度为30°，周期为5 s，采样频率为50 Hz，机器人参数如表1所示。

表1 机器人模型参数表

采用遗传算法求解各方程条件数最小值，其相关参数如表2所示。

表2 遗传算法主要参数表

由于观测矩阵满秩是条件数衡量方程解误差的前提，故仅对满足秩要求的方程进行最小条件数计算，结果如表3所示。

表3 机器人模型最小条件数统计表

由计算结果，可得各模型优化后的激励轨迹曲线，如图6、图7所示。

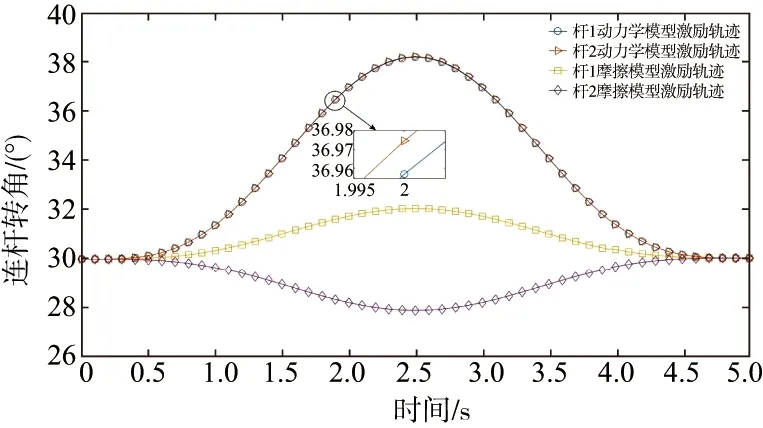
图6 单杆运动各杆激励轨迹图

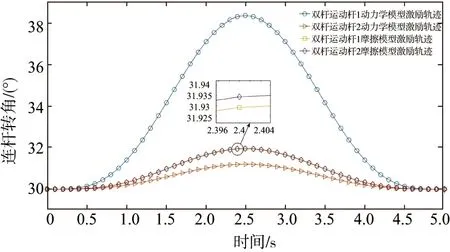
图7 双杆运动各杆激励轨迹图

由仿真计算结果，可得如下结论：

1)各模型最小条件数均较小，满足要求；

2)依条件数大小，先单独运动各杆以辨识摩擦参数，后运动杆2辨识部分惯性参数，最后同时运动两杆，辨识剩余参数；

3)轨迹范围大小与条件数不一定成正比；

4)采样频率与运动周期应取较大值，否则条件数将较大。

5 结语

本文提出基于关节转矩传感器重力补偿的柔性关节机器人动力学模型。在模型可线性化以及辨识方法为最小二乘法的前提下，本文制定了基于矩阵秩与条件数的参数分步辨识策略，并针对线性方程，说明了进行分步辨识的判据、确定辨识顺序的方法以及降低误差的途径等。该策略同样可用于其他领域线性方程组的参数辨识。