接触式机械密封孔隙率及密封间隙研究
於秋萍,孙见君,马晨波
(南京林业大学 机械电子工程学院,南京 210037)
0 引言
机械密封失效最主要和最直观的表现是在给定的工作条件下,提前出现泄漏超标的现象,而泄漏是由界面间的泄漏微通道和流体的流动阻力决定的,因此前人展开了大量关于泄漏微通道[1-3]和微通道内流体流动[4-6]的研究。其中,存在泄漏微通道是产生泄漏的前提,而泄漏微通道构成与否取决于密封界面的孔隙率;另一方面,孔隙率也影响着界面间的孔隙分布,从而影响着流体的流动。因此,孔隙率对密封界面的泄漏特性研究具有重要意义。
关于粗糙表面的接触,目前主要有2种分析方法:(1)按照双粗糙表面进行弹塑性变形分析,研究两表面的接触力、接触刚度、摩擦热等[7-9];(2)将两粗糙表面的接触简化为一粗糙表面与一刚性光滑平面的接触,从而进行接触力、接触面积、接触压力分布等[10-12]研究。然而,这2种方法的适用场合却没有明确地给出界定,也没有具体针对接触式机械密封进行研究。
本文针对接触式机械密封,求解了密封面的逾渗阈值,分析了表面的接触状态,利用MATLAB计算出了两粗糙表面接触时的密封间隙高度比和孔隙率,并分析了表面形貌对它们的影响,旨在为机械密封界面泄漏机理研究和接触力学分析提供新思路。
1 密封界面孔隙率及接触状态
1.1 孔隙率
对于接触式机械密封而言,若两密封表面均十分光滑,则两表面间的接触属于完全接触,密封界面不存在泄漏通道;然而,实际的密封表面并不光滑,存在着大量大小不一的微凸体,密封面的接触并不理想,接触界面间分布着大大小小的孔隙和孔隙团,当这些孔隙团连通形成贯穿密封界面的微通道后,在压差的作用下被密封介质便会沿着微通道从腔室的一侧泄漏到另一侧。
接触式机械密封的密封界面凹凸不平,根据体积平均化的思想,可以在机械密封界面上取一个单元来表征整个密封多孔界面。
对于底面为L×L、高度为h(即密封间隙)的长方体单元,其孔隙率与骨架体积占有率之和为1,即:

式中φ0——初始孔隙率;
V ——骨架体积;
V0——多孔密封界面总体积。
当机械密封承受载荷pc作用时,密封界面由于受力会产生接近量δ,密封界面的高度由h减小至h-δ,载荷作用下的单元体如图1所示,此时,密封界面上计算单元体的体积由V0=L2h变为V0'=L2(h- δ)。

图1 载荷作用下的密封界面计算单元体Fig.1 Calculating element of the sealing interface under load
在加载过程中,密封界面内的骨架会发生变形,但体积几乎不变,始终为(1-φ0)V0,而孔隙体积则变为V0'-V,因此,加载后的密封界面孔隙率变为:

可以看出,加载后的孔隙率与初始孔隙率、密封间隙及压缩量有关,这些参数的求解至关重要。
1.2 密封界面的接触
对于机械密封的接触研究,大多是在GREENWOOD等[13]研究的基础上,对两个粗糙面进行简化,将其中较光滑的表面简化为一光滑刚性平面[14],此时2个表面的接触状态如图2所示,骨架体积可由函数积分求得。其中,下标r-f表示粗糙面与光滑平面接触。
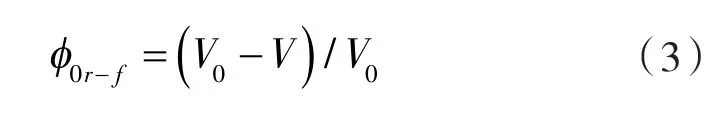
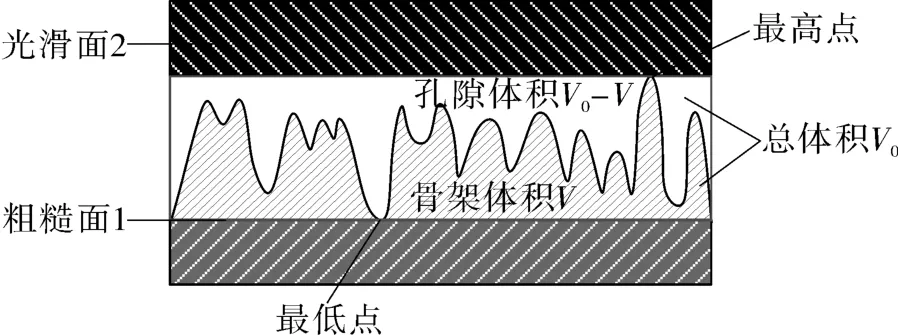
图2 光滑平面与粗糙面的接触示意Fig.2 Schematic diagram for the contact of smooth plane and rough surface
然而,实际状况为密封界面并不完全光滑,2个接触面上都存在微凸体,如图3所示。2个表面上的骨架体积可分别由函数积分求得。其中,下标r-r表示粗糙面与粗糙面接触。


图3 两粗糙面的接触示意Fig.3 Schematic diagram for the contact of two rough surfaces
进行接触分析时,研究对象一般是对单个/单对微凸体。如图2,3所示的表面接触用最大微凸体表示,如图4,5所示。
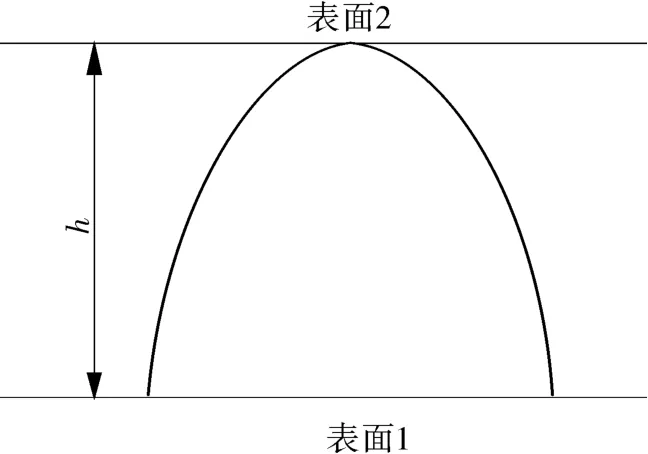
图4 光滑平面与粗糙微凸体的接触示意Fig.4 Schematic diagram for the contact of smooth plane and rough asperity

图5 2个粗糙微凸体的接触示意Fig.5 Schematic diagram for the contact of two rough asperities
对于图4所示情形,密封间隙h为面1、面2上综合微凸体的高度(h12+h22)1/2;而对于图5所示的更为真实的接触状态,密封间隙比2个表面上最大微凸体高度之和(h1+h2)要小,研究其密封间隙h以及h/(h1+h2)的比值(简称密封间隙高度比)是分析密封界面接触状态、获得密封界面孔隙率的前提。为了更接近实际,后文研究的是图3和5的接触情况。
2 逾渗阈值
逾渗是由 BROADBEND 等[15]在 1957年提出的,指的是使得网格上的未被占座(即孔隙)刚好能够从密封面的一端通向另一端时的现象,近年来被广泛应用于密封面的研究中[16-18]。
对于密封界面,假设微立方体为孔隙的概率为P,相应的孔隙率为φ,则骨架的概率为1-P=1-φ。逾渗理论认为,每个微立方体为孔隙或骨架的概率是随机且相互独立的,孔隙最大团的大小和分布是孔隙率φ的函数,一旦孔隙率φ达到特定的临界值φc,即当φ=φc时,这一最大孔隙团将会贯穿多孔密封界面的两侧,形成泄漏微通道,此时的临界孔隙率φc即为封界面的逾渗阈值。
由于逾渗阈值与网格数量密切相关,因而利用MATLAB编程建立m×m×k(k为网格层数,m×m为单层的网格数量)个网格微立方体多孔界面模型,求解密封界面的逾渗阈值。为了获得固定网格层数下网格数量对逾渗阈值的影响,计算了不同网格数量下的逾渗阈值。结果表明,当网格层数一定时,网格数量大于300×300后,再增加网格数量不会改变逾渗阈值,如图6所示,证明了逾渗阈值具有网格无关性。图6中的纵坐标逾渗概率表示最大孔隙团占网格总数的比值,当孔隙率小于逾渗阈值时,逾渗概率接近于0,达到逾渗阈值后,逾渗概率突然剧增。
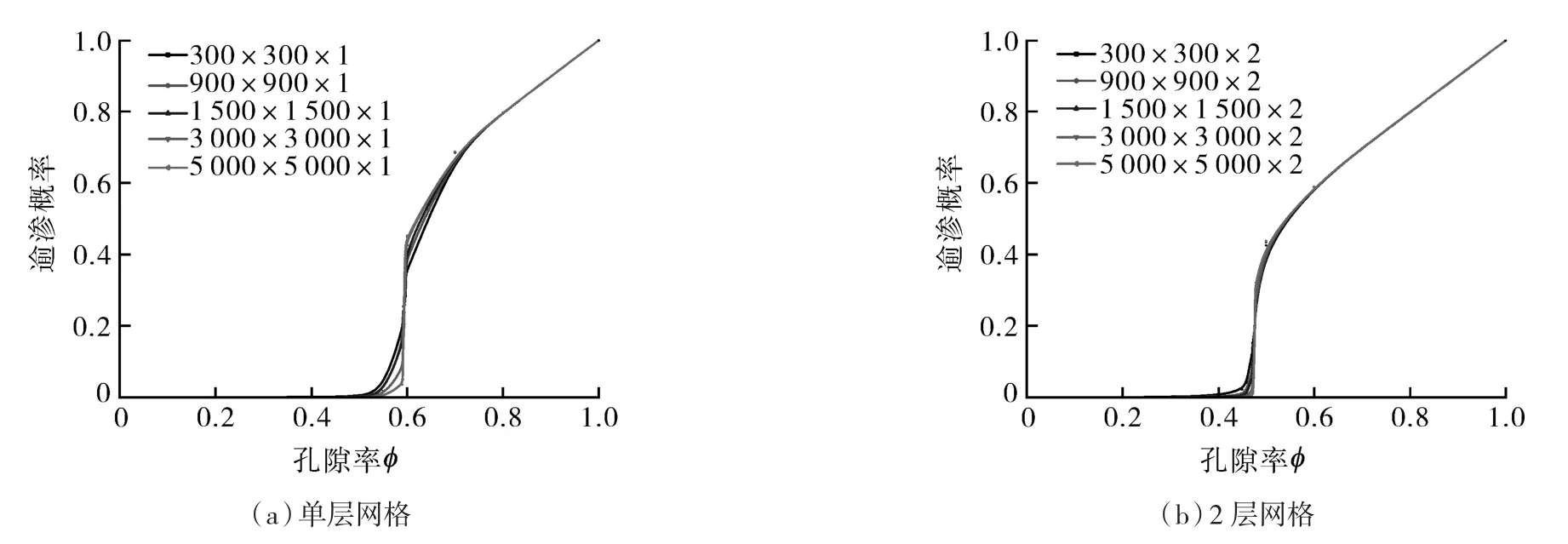
图6 不同网格数量下的逾渗阈值Fig.6 Percolation threshold under different grid number
密封界面在不同网格层数下的逾渗阈值,则如图7所示。可以看出,随着密封界面网格层数的增加,对应的逾渗阈值减小:当网格层数为1时,逾渗阈值φ1=0.593,这与理论值相符[19];当网格层数为 2,3,4,5 时,逾渗阈值分别为φ2=0.475、φ3=0.425、φ4=0.402、φ5=0.386;当网格层数无限大时,逾渗阈值接近 0.312[20]。

图7 不同网格层数下的逾渗阈值Fig.7 Percolation threshold under different grid layers
网格层数反映了密封界面的复杂程度。当网格层数为1时,密封面在高度方向上只有一种泄漏可能;随着网格层数的增加,密封面在高度方向上的泄漏概率越来越大、逾渗点尺寸越来越小,从而流体的流动情况也越来越复杂,如图8所示。也就是说,当孔隙率大于0.593时,密封面会泄漏;当孔隙率小于0.312时,密封面不会泄漏;当孔隙率处于0.312~0.593之间时,网格层数越多,密封面在高度方向上被划分得越多,则泄漏情况越复杂。
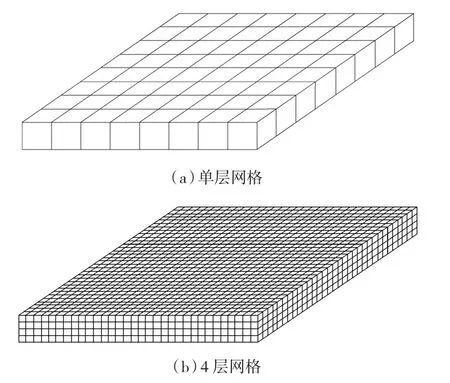
图8 不同网格层数时的密封界面间微凸体分布Fig.8 Distribution of asperities within sealing interface under different grid layers
3 机械密封表面的分形表征
3.1 机械密封表面的W-M函数
大量研究[21-25]表明,接触式机械密封的动、静环表面及其运行后的磨损表面均具有分形特征,其表面轮廓形貌可以用Weierstrass-Mandebolt函数(即W-M函数)[26-27]进行数学表征:


根据式(7),利用MATLAB软件可模拟出单个随机粗糙表面,如图9所示;也可根据2个表面刚好接触时的高度关系,模拟2个粗糙表面的初始接触状态,如图10所示。

图9 单个粗糙表面的MATLAB模拟Fig.9 MATLAB simulation of single rough surface

图10 2个粗糙表面接触的MATLAB模拟Fig.10 MATLAB simulation of the contact of two rough surfaces
3.2 密封界面孔隙率的数值计算表达



4 密封间隙高度比及孔隙率的计算和分析
利用MATLAB进行编程,求出动、静环密封界面的密封间隙h、密封间隙高度比h/(h1+h2)和初始孔隙率φ0。表面形貌的参数取值:
D:1.3,1.35,1.4,1.45,1.5,1.55,1.6;
G:1×10-11,9×10-11,1.7×10-10,2.5×10-10,3.3×10-10,4.1×10-10,4.9×10-10m。
4.1 密封间隙高度比
在分析分形维数D、尺度系数G对密封间隙高度比的影响时,采取单因素分析法:分析尺度系数G的影响时,令D1=D2=1.45,一个表面的尺度系数固定,另一表面的尺度系数在1×10-11~4.9×10-10m之间变化;分析分形维数D的影响时,令G1=G2=2.5×10-10m,一个表面的分形维数固定,另一表面的分形维数在1.3~1.6之间变化。结果如图11,12所示。
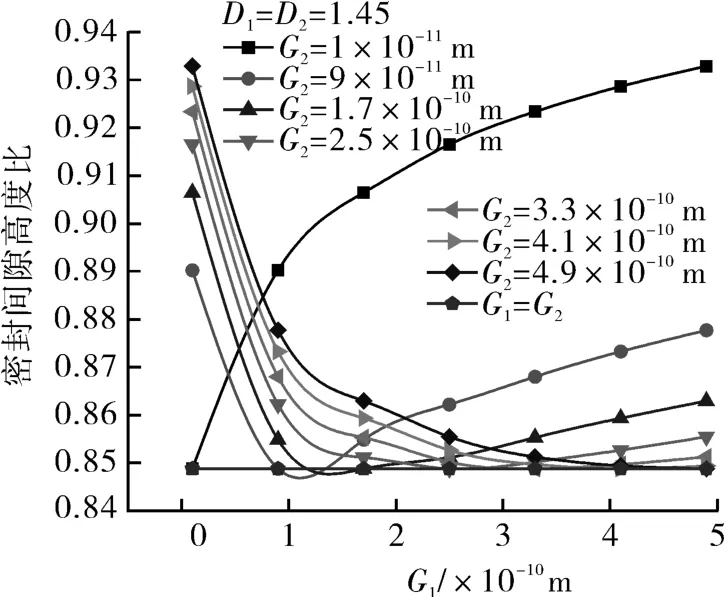
图11 密封间隙高度比随G的变化Fig.11 Change of ratio of seal clearance to seal height with G
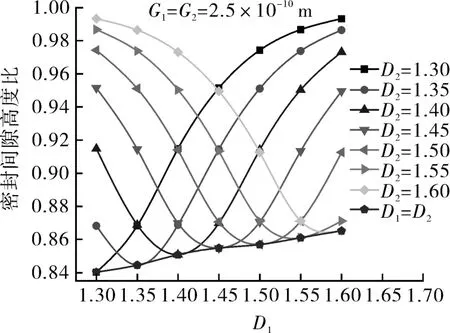
图12 密封间隙高度比随D的变化Fig.12 Change of ratio of seal clearance to seal height with D
由图11可以看出,当两个接触表面的尺度系数相同,即G1=G2时,密封间隙高度比没有变化,始终保持在0.849左右,侧接触特征明显。尺度系数G表征的是表面轮廓的幅值,但对表面轮廓的形状或复杂程度几乎没有影响,当两表面的尺度系数相同时,表面轮廓的幅值近似,微凸体的大小和形状相似,容易啮合;在相同的分形维数下,尺度系数的增大不会改变表面轮廓的形状,因而密封间隙高度比不变。2个表面的尺度系数相差越大,表面轮廓的幅值相差越大,微凸体越不容易啮合,造成密封间隙高度比增大,越接近于粗糙面与平面的接触。
由图12可以看出,当2个接触表面的分形维数相同,即D1=D2时,密封间隙高度比在0.84~0.86之间变化,侧接触特征明显。分形维数表征的是表面轮廓的不规则程度,当2个表面的分形维数相同时,表面轮廓的不规则程度相近,2个表面上的微凸体更容易嵌入对方;在相同的尺度系数下,分形维数的增大会削弱表面的粗糙程度,使表面变得更平滑,微凸体曲率半径增大,啮合程度不如更小的微凸体,因而密封间隙高度比更大一些,但变化并不大。2个表面的分形维数相差越大,表面轮廓的不规则程度差距越大,表面上的微凸体越不容易啮合,密封间隙高度比就越大,因而越接近于粗糙面与平面接触。当分形维数在1.3~1.6之间变化时,密封间隙高度比随D的变化呈近似对称分布。
综合图11和12可以看出,分形维数对密封间隙高度比的影响比尺度系数更大,2个表面的分形维数和尺度系数相同/相近时,侧接触特征明显;2个表面的分形维数和尺度系数相差越大,越接近于粗糙面与平面接触。
4.2 密封界面孔隙率
以D1=D2、G1=G2的2个粗糙面为分析对象,研究其在侧接触状态下的孔隙率。
首先需要验证侧接触状态下初始孔隙率的数值计算表达式,即式(12)的正确性,为此对W-M函数模拟计算获得的初始孔隙率、根据式(12)、式(13)计算所得的初始孔隙率进行整理和比较,结果如图13所示。可以看出,当2个粗糙面的分形维数和尺度系数相同时,根据粗-粗接触模型得到的数值计算值更接近模拟值,最大相对误差不超过5%,而根据粗-平接触模型得到的数值计算值与模拟值的相对误差为10.5%~15.5%。

图13 不同方法获得的初始孔隙率Fig.13 Initial porosity obtained by different methods
本文以 D1=D2=1.45,G1=G2=2.5×10-10m 为例(此时的初始孔隙率为0.575 53,密封间隙为5.615 35 μm),对应图7和式(2),计算其不同网格层数下的临界压缩量(临界压缩量表示在该压缩量下,密封介质在该网格层数下不会泄漏),结果见表1。可以看出,当压缩量大于2.150 88 μm后,孔隙率小于0.312,密封面不会泄漏。
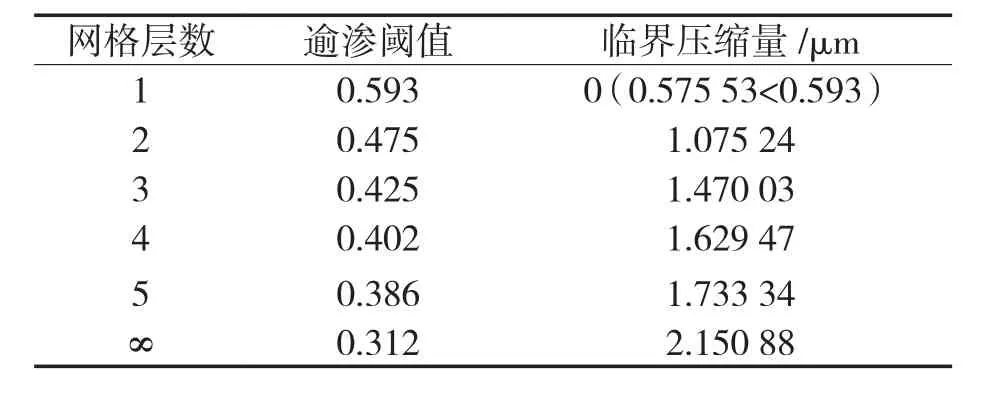
表1 不同网格层数下的临界压缩量Tab.1 Critical compression under different grid layers
5 结论
(1)基于逾渗理论,利用MATLAB获得了不同网格层数下的逾渗阈值,可为密封面是否泄漏提供判据。
(2)通过W-M函数及其变式,利用MATLAB模拟得到了各表面形貌参数下2个粗糙表面接触时的密封间隙高度比等参数,并获得了密封间隙高度比随尺度系数和分形维数的变化。
(3)接触式机械密封界面可简化为一粗糙面与一平面的接触,也可简化为两粗糙表面的侧接触。两表面的形貌参数相同或相近时,侧接触特征明显;两表面的形貌参数相差越大,越接近于粗糙面与平面接触。研究结论为粗糙表面的接触力学分析提供了参考。
(4)对于侧接触特征明显的接触表面,利用接触面积分布密度函数和孔隙率概念,可以较准确地表征密封面间的初始孔隙率,进而求得各逾渗阈值下的临界压缩量,进一步验证了侧接触的正确性,也为表面的泄漏控制提供了依据。

