基于小信号模型的风电场同调等值理论

董文凯，王海风

(1. 电力系统及发电设备控制与仿真国家重点实验室(清华大学电机系)，北京100084；2. 四川大学电气工程学院，成都 610065)

0 引言

风电大规模并网在缓解能源和环境危机的同时，也会造成电力系统抗小干扰能力降低[1 - 2]。由于风电场规模扩大，大型风电场内通常具有数百台风电机组(wind turbine generator, WTG)，在分析并网风电场小干扰稳定性时，如果直接对所有WTG采用详细模型，会导致模型阶数高、问题分析和计算求解工作量大。因此，目前常采用风电场动态等值模型对并网风电场小干扰稳定性进行分析与研究。

同调等值是目前风电场动态等值中的常用方法[3 - 9]。该方法首先根据风电场内各WTG的型号以及输入风速、端电压和转子转速等的相似程度，对WTG进行聚类，将风电场划分为几个由型号相同、且运行状态相似的WTG构成的风电机群(后文中称为同调风电机群)，再对各风电机群进行单机等值，即用几台等值WTG代表整个风电场。因此，风电场同调等值也称为多机等值[4]。对于风电机群的聚类，常采用k均值聚类、c均值聚类和支持向量机等方法[3 - 9]。对于等值WTG，其容量采用风电机群总容量，参数通常由容量加权平均法[3 - 8]或参数辨识法[9]确定。

容量加权平均法以风电机群内各WTG的额定容量与风电机群总容量的比值为权重，计算各WTG参数的加权平均值作为等值WTG参数[3 - 8]。该方法应用简单、计算量小，但是其未考虑等值前后系统动态交互与特征值信息的一致性，用于小干扰稳定性分析的有效性与成立条件还有待进一步探讨[9]。为提高等值模型的准确性，文献[9]将参数辨识法引入风电场同调等值。等值WTG参数的辨识，本质上可看作对一个优化问题的求解；其目标函数为：相同工况或外部扰动作用下，等值WTG的输出特性和原风电机群整体的输出特性误差最小；待求量为等值WTG参数[9 - 13]。由于参数辨识涉及非线性优化问题的求解，一般需采用智能优化算法[9 - 13]。

综上所述，当前已有大量研究对风电场同调等值方法进行了深入探讨，并构建起了一套较为完善的方法体系，具有一定的实际应用价值。同调等值理论认为：在外部电力系统扰动(后文简称为外部扰动)作用下，风电场内型号相同且运行状态相似的WTG会对外表现出一致的动态特性，且整体动态输出特性可通过一台WTG反映[3 - 8,14]，这一现象或认识可看作风电场同调等值思想的理论基础；而当前未见有文献对其理论依据进行过探讨或证明。为帮助完善风电场同调等值的理论基础，本文中基于小信号模型，探讨了上述现象出现的原因及成立条件。为此，首先建立了风电机群全阶线性化模型。然后，在风电机群内各WTG线性化模型相似的条件下，推导了风电机群线性化模型的等效解耦，分析了风电场同调等值的理论依据。最后，通过仿真算例验证了所提方法和所得结论的有效性。

1 风电机群全阶线性化状态空间模型

图1为N台WTG构成的风电机群的示意图。外部电力系统包括交流电网以及风电场其他部分，图1中WTGk的线性化状态空间模型如式(1)所示。

图1 并网风电机群结构图Fig.1 Configuration of a grid-connected group of WTGs

(1)

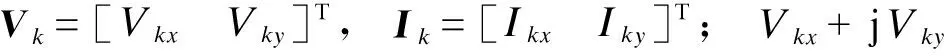
根据附录A中的推导，不考虑线路电阻，图1所示并网风电机群的网络方程为：

ΔV=ΖwΔI+ΔVcM

(2)

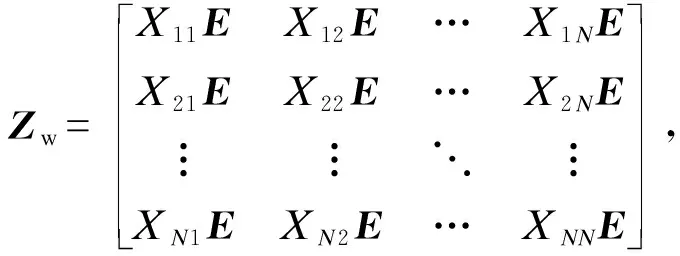
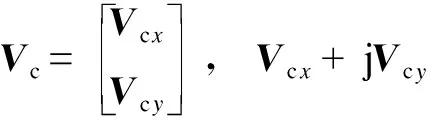
根据式(2)中的矩阵Zw， 可建立风电机群连接电抗矩阵，如式(3)所示。

(3)

式中RN×N表示N×N的实矩阵。Xw中的元素可根据如下原则确定：1) 对角线元素Xkk,k=1,2,…,N为连接WTGk到母线C的线路电抗之和；2) 非对角线元素Xjk,j,k=1,2,…,N,j≠k为连接WTGj和WTGk到母线C的线路公共部分电抗之和。

由式(1)可得：

(4)

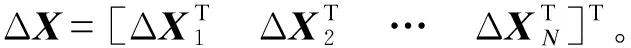
将式(2)代入式(4)，整理可得图1所示并网风电机群的全阶线性化状态空间模型为：

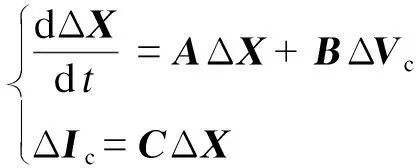
(5)

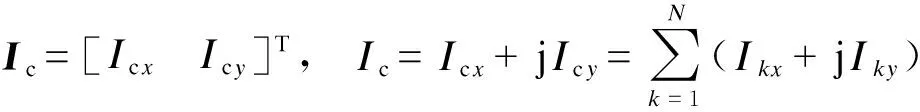
2 风电场同调等值理论分析

在第1节的基础上，本节将借鉴模式分析理论中模式分解的思路[14 - 15]，推导风电机群线性化模型的等效解耦，并类比模态、可控性和可观性的定义，分析风电场同调等值的理论依据。为此，首先在2.1节对模式分析的相关理论作简要介绍。

2.1 模式分析的基本理论

考虑m阶动态系统，其线性化状态空间模型如式(6)所示。

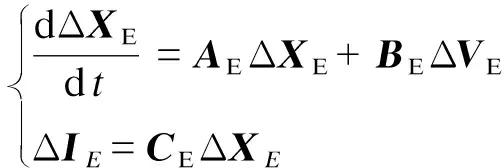
(6)

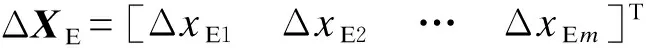
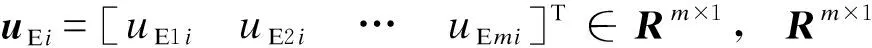
(7)

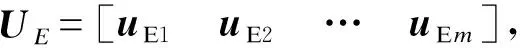
定义如式(1)变量变换。

ΔXE=UEΔYE

(8)

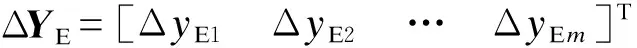
将式(8)代入式(6)并结合式(7)可得：

(9)

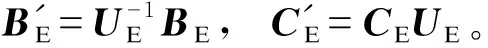
对比式(6)和式(9)所示系统得到以下结论。

1)矩阵AE一般为非对角矩阵，式(6)状态空间表示形式中，状态变量ΔxEi之间存在交叉耦合[14]；引入式(8)所示变量变换，采用状态变量ΔyEi描述系统动态特性，可消除状态变量间的交叉耦合，使得ΔyEi的时域响应与λEi直接关联(i=1,2,…,m)，得到更为理想、便于展开分析的建模表示形式。

2)式(8)中，特征向量uEi中的元素uEki反映了ΔyEi的动态响应被激发时原始状态变量ΔxEk的活跃程度(k=1,2,…,m)，uEi被称为λEi的模态[14]。若uEki和uEji的幅值和相角均相同，ΔyEi的动态响应被激发时，ΔxEk和ΔxEj的活跃程度相同；若uEki和uEji的幅值相同相角相差180 °，ΔyEi的动态响应被激发时，ΔxEk和ΔxEj的活跃程度相互抵消。

3)式(9)中，若B′E中第i行元素为0，则ΔyEi的动态响应不受输入ΔVE影响，即ΔyEi的动态特性是“不可控的”；若C′E中第i列元素为0，则ΔyEi的动态响应不会体现在输出ΔIE中，即ΔyEi是“不可观的”。B′E和C′E分别被称为模式的可控性和可观性矩阵[14 - 15]。

2.2 风电机群线性化状态空间模型等效解耦

为便于研究风电场同调等值理论依据、推导同调风电机群单机等值模型的表示形式，首先在本节推导同调风电机群全阶线性化模型的等效解耦。在推导时，首先假设风电机群内各WTG线性化状态空间模型相同，即：

Ak=Aw,Bk=Bw,Ck=Cw,k=1,2,…,N

(10)

对于式(10)所示的假设作进一步解释如下。

1)实际中，一个风电场通常采用来自同厂家且同型号的WTG，各WTG初始参数设定相同[16]；

2)在风电场同调等值中，首先需根据各WTG输入风速、端电压和输出功率等的相似程度，将风电场划分为几个由型号相同且运行状态相似的WTG构成的风电机群[3 - 8]；

3)由于风电机群内WTG初始参数设定相同且运行点相似，各WTG线性化模型近似相同，在理论推导中可假设其线性化模型相同。

将式(10)代入式(5)可得：

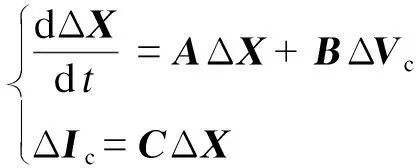
(11)

式中：

下面将借鉴2.1节中由式(6)—(9)的变换思路，推导式(11)所示动态系统的等效解耦。

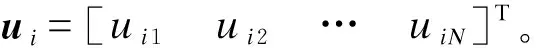
UTXwU=diag[λi]

(12)

借鉴式(8)所示变量变换，对式(11)所示风电机群线性化状态空间模型引入如式(13)的变量变换。

ΔX=UnΔY

(13)

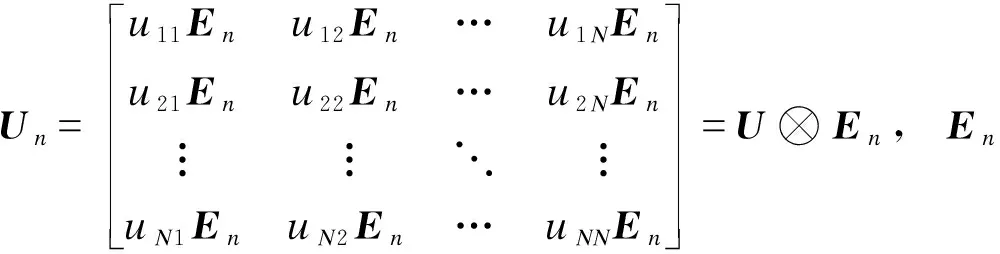
将式(13)代入式(11)，如式(14)所示。

(14)

根据克罗内克乘积的性质，结合式(12)，可得：

式中：ΕN为N×N的单位矩阵；diag[Aw+λiA0]为对角线元素为(Aw+λiA0)，i=1,2,…,N的分块对角矩阵。

由式(14)和式(15)，通过引入式(13)所示变量变换，可将式(11)所示的风电机群线性状态空间模型转换为如式(16)表示形式。

(16)

由式(11)—(16)的推导过程，结合2.1节对模态、可控性和可观性的介绍，可作如下分析。

1)式(16)中，当采用状态向量ΔY描述风电机群动态特性时，状态向量ΔYi(i=1,2,…,N)之间没有交叉耦合，原风电机群的动态特性可通过如下N个相互独立的等效子系统反映。

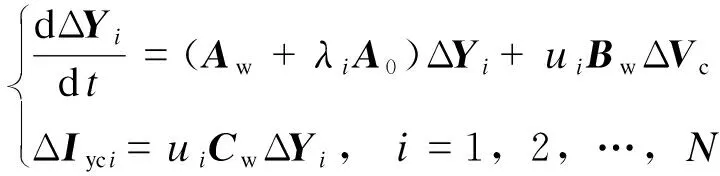
(17)

式中ΔIyci为第i个等效子系统的输出向量。

式(17)也可写为如下形式。

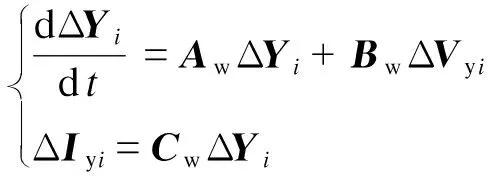
(18a)

ΔVyi=λiEΔIyi+uiΔVc,ΔIyci=uiΔIyi

(18b)

根据式(18)，第i个等效子系统可看作是由1台WTG经电抗为λi的线路并网构成的。其中WTG的线性化模型仍为(Aw,Bw,Cw)， 但是动态过程中，WTG与母线C接口间的潮流需按照式(18b)计算。由此可得，式(16)所示系统的结构如图2所示。

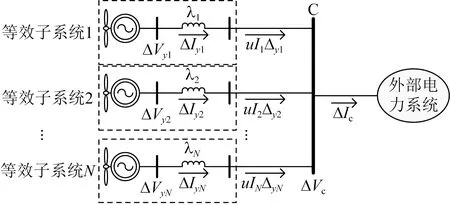
图2 等效子系统结构图Fig.2 Configuration of equivalent subsystems

2) 参照2.1小节中模态的定义，式(13)中特征向量ui中的元素uki反映了ΔYi的动态响应被激发时原始状态向量ΔXk的活跃程度。

3)参照2.1小节中可控性和可观性的定义，由式(16)—(17)可知，uiBw和uiCw分别反映了第i个等效子系统动态特性的可控性和可观性；若ui=0， 则第i个等效子系统是不可控、且不可观的。

2.3 风电场同调等值理论分析

风电场同调等值中认为，1个由型号相同且运行状态相似的WTG构成的风电机群可由1台等值WTG代表；对此，本节将基于小信号模型，探讨其理论依据并给出其成立的条件。

在式(10)假设基础上，如果进一步假设风电机群内的N台WTG对称连接至外部电力系统，具体结构如图3所示(xc≥0)。此时，根据第1节给出的风电机群连接电抗矩阵的形成原则得到式(19)。

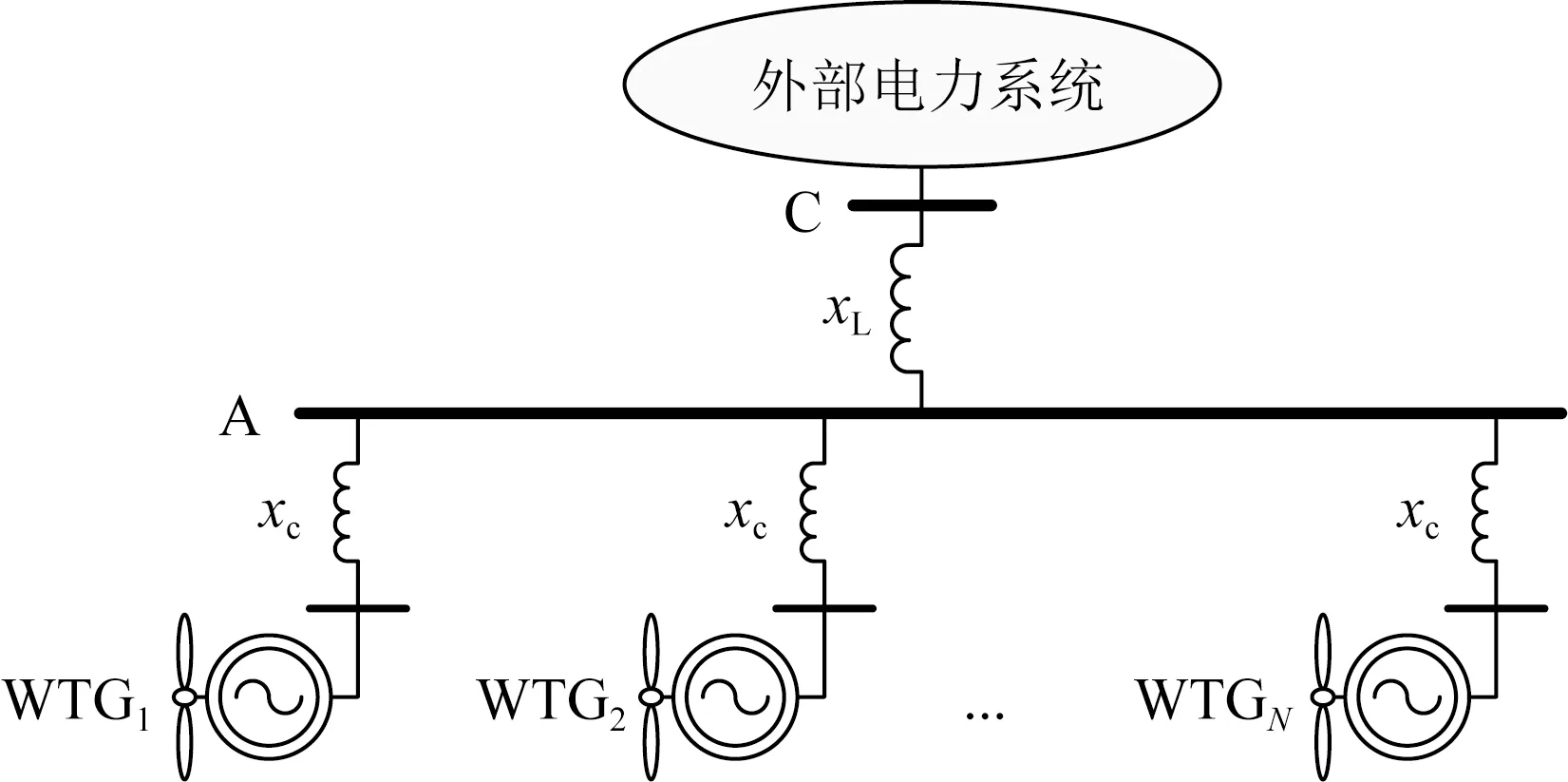
图3 风电机组对称连接构成风电机群示意图Fig.3 Configuration of a group of WTGs in symmetrical connection

(19)

易证明，式(19)中矩阵Xw的特征值为：λi=xc,i=1,2,…,N-1和λN=xc+NxL； 对其特征向量有：

ui=0,i=1,2,…,N-1

(20a)

(20b)

由式(20)，结合2.2小节的分析2)和3)，可作如下讨论。

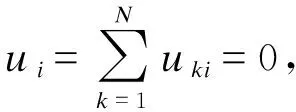
2)由式(20a)，前N-1个等效子系统的可控性和可观性均为0。前N-1个等效子系统所反映的动态特性在外部电力系统中是不可观测的，这与讨论1)中所得结论是一致的，即前N-1个等效子系统反映了风电场内部的动态特性，为WTG间的相对活动、且相互抵消，不会体现在外部电力系统中。

3)由式(20b)中给出的uN的表达式，当ΔYN的动态响应被激发时，ΔXk(k=1,2,…,N)活跃程度相同；因此，外部扰动作用下，风电机群内各WTG对外部电力系统表现的动态特性是一致的。

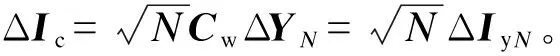
综上，若一风电机群满足式(10)和式(19)所示假设条件，则外部扰动作用下，该风电机群内各WTG对外部电力系统表现出一致的动态特性、且其整体动态输出特性可通过1台等值WTG反映。

通常情况下，上述假设条件难以完全成立，但是若一风电机群可满足：

条件a：风电机群内各WTG线性化模型近似相同，即：(A1,B1,C1)≈(A2,B2,C2)≈…≈(AN,BN,CN)≈(Aw,Bw,Cw)，N为风电机群内WTG的数量；

则外部扰动作用下，该风电机群内各WTG对外部电力系统表现的动态特性基本一致、风电机群整体动态输出特性可通过1台等值WTG近似反映。

对于风电场同调等值中条件a和条件b的可成立性作分析如下。

1)对于条件a：结合2.2小节对式(10)所示假设的3点解释，可认为风电场同调等值中，合理有效地对风电场内的WTG进行聚类，可保证风电机群内各WTG线性化模型近似相同。

2)对于条件b：考虑到同调等值中，通常将输出功率和端电压近似的WTG聚类为一个风电机群；可认为风电机群内部集电网络上的电压降落或功率损耗造成的各WTG稳态运行点差异不大，各WTG可近似看作对称连接至外部电力系统。

由此，基于小信号模型，从理论上解释了为何可根据WTG运行状态的相似程度，将风电场划分为几个由型号相同且运行状态相似的WTG构成的风电机群，再对各风电机群进行单机等值。以上条件a和条件b，对于风电机群的划分具有一定指导意义。根据以上分析1)和2)，WTG的输出功率(或输入风速)和端电压为风电机群划分中的重要聚类指标。当然，为进一步明确风电场分群标准，还需在上述条件a的基础上继续探讨型号相同的条件下，稳态运行点差异造成WTG动态特性差异的量化衡量指标。

根据此前的分析，若图1所示风电机群满足条件a和条件b，则其整体动态输出特性可通过式(18)中第N个等效子系统反映；对于前N-1个等效子系统，由于其动态在外部电力系统中的可控性和可观性近似为0，可将其看作恒定电流源。由此，图2可进一步简化为图4所示形式，即风电机群整体动态输出特性可通过1台WTG反映。图4中WTG的线性化模型仍为(Aw,Bw,Cw)， 因此，其模型和参数与原风电机群内WTG的模型和参数相同。但是，动态过程中，图4中的潮流关系需按照式(18b)计算。对于WTG的输入风速，本文中取原风电机群内各WTG输入风速的平均值。

图4 风电机群单机等值模型示意图Fig.4 Configuration of a single-machine equivalent model of a group of WTGs

本节借鉴传统模式分析的思路，通过引入一变量变换，推导了风电机群线性化模型的等效解耦，将其转换为一更为理想、便于展开分析的表示形式；

并借鉴模态、可控性和可观性的定义，重点分析了一风电机群内的WTG可对外表现出一致的动态特性、且整体动态输出特性可由1台WTG反映的原因和成立条件。所作理论分析对于理解风电场这一可看作由多个子系统(WTG)经复杂网络互联构成完整系统的动态特性及其分布规律具有很好的指导意义，也为风电场动态等值提供了理论支撑。基于推导结果，也获得了一种风电机群单机等值表示形式。

等效解耦的核心是通过引入一组新的用来描述系统动态特性的状态变量，得到一种新的风电机群建模表示形式，这一过程并未改变系统的动态特性，所得等效子系统仍保留了原系统的动态交互信息。考虑到当前大量理论研究与工程实践均表明：风电场内部WTG之间的动态交互以及风电场与外部电力系统间的动态交互作用导致系统容易在扰动作用下出现功率振荡、尤其是次同步振荡现象[2,17]，而且此类动态交互均属于小干扰动态的范畴[18]，本文所作理论推导、所得单机等值表示形式也具有一定的应用与推广价值，具体说明如下。

本文所得单机等值表示形式，可推广应用于风电场规划阶段进行小干扰稳定性检验。例如，当风电场内所有WTG均处于额定运行状态时，此时风电场输出功率最大，对风电外送系统功率输送能力要求最高，如果交流系统无法提供足够的无功和电压支撑，则风电场容易在扰动作用下产生功率振荡现象[2,17]，对此应在风电场规划阶段重点考虑[19]。而且，实际中同一风电场内通常采用来自同一厂家且同一型号的WTG，在规划阶段可采用典型模型和参数，进行小干扰稳定性检验[19]。此时，由于稳态功率输出相同，WTG的线性化模型也是近似相同的，即风电场是满足条件a的。对于条件b，考虑到风电场内部集电网络主要用于功率汇集，其中的稳态潮流应远小于线路的极限传输功率[20]，系统无功和电压损耗主要源自风电外送线路，尤其是风电场经长线路弱联络接入交流系统时。因此，式(3)所示风电场连接电抗矩阵，可看作由xL主导的矩阵；结合2.3小节基于式(19)—(20)的分析，风电场整体动态输出特性主要体现在式(18)所示的第N个等效子系统中，即风电场并网运行的主导振荡模式可由第N个等效子系统反映。基于第N个等效子系统，可通过分析一单机并网系统的小干扰稳定特性，获得1个N(N为任意正整数)机风电场的小干扰稳定性信息，从而有效降低风电场规划阶段小干扰稳定性检验的工作量，有利于对比多种设计方案并选取最佳方案。

图4所示风电机群单机等值表示形式的有效性以数学模型的理论推导为依据，其中保留了系统中的动态交互信息，适用于风电并网系统小干扰稳定性分析，且应用简单，对于具体的风电场，在完成风电机群划分后，可根据各风电机群的具体表示形式，代入图4，建立其单机等值模型，其中仅需对动态过程中的潮流计算关系按照式(18b)进行修正，无须对等值WTG参数进行求解。相对参数辨识法而言，等值建模效率更高，尤其是考虑多种不同运行状态，分析风电场小干扰稳定性时。但是，本文偏重理论分析，为将图4所示单机等值表示形式有效应用于风电场同调等值，还需对如下问题作进一步探讨：1)本文中仅给出了一个风电机群的单机等值表示形式，考虑多个风电机群串并联构成完整风电场的动态等值表示形式还有待进一步明确；2)实际中，风电场运行状态复杂多变，不同运行状态下，风电机群划分形式可能也不尽相同，对于如何确保所得单机等值表示形式可在不同运行状态间灵活切换，也还有待进一步探讨与明确。

3 算例分析

算例系统如图5所示，风电场内采用永磁直驱风机(permanent magnet synchronous generator, PMSG)，其结构见附录B。PMSG参数来自文献[21 - 22]，具体见附录B，并采用文献[21]中给出的模型；同步发电机(synchronous generators, SGs)采用文献[23]中给出的20阶模型和参数，仿真软件采用Matlab。本节算例1—3将分别针对2.3小节给出的条件a和条件b同时成立、条件a不成立、条件b不成立3种情况展开分析，算例4给出结合实际风电场的进一步分析。

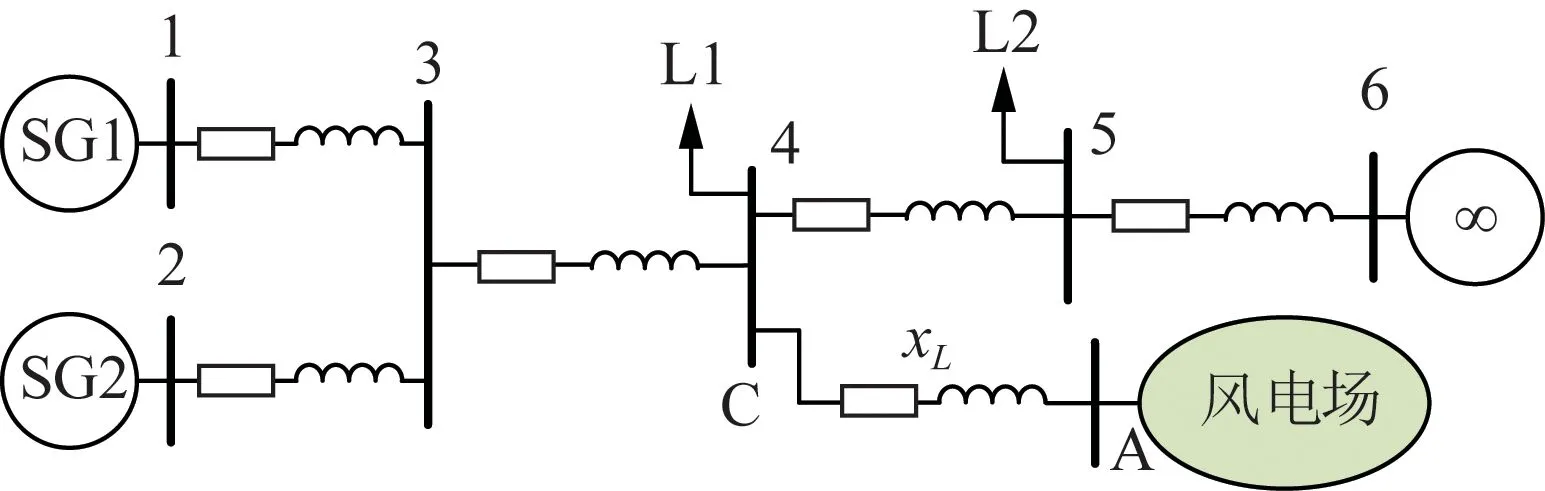
图5 风电场并网系统算例Fig.5 An example of wind farm integrated power system

3.1 算例1

本算例中风电场结构如附录B图B1所示，其PMSG1-PMSG20均采用附录B表B1中的参数。考虑风速空间分布差异，PMSG1稳态有功输出0.1 p.u.，功率因数0.98，其余PMSG稳态功率输出在此基础上随机变化，且最大变化范围为±10%。因此，各PMSG运行点近似且参数设定相同，2.3小节中的条件a成立。

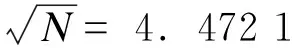
根据2.3小节的分析，外部扰动作用下，风电场内各PMSG对外表现的动态特性基本一致、且整体输出特性可通过一台等值WTG近似反映。

表1 风电场连接电抗矩阵特征值特征向量计算结果1Tab.1 Eigenvalues and eigenvectors of the network reactance matrix of the wind farm 1

首先，采用风电场全阶模型，对算例系统进行模式分析，得到风电场振荡模式在复平面上的分布如图6所示。根据参与因子，图6(a)—(d)中所示的振荡模式依次为：网侧换流器(grid-side converter，GSC)d轴电流内环模式、GSCq轴电流内环模式、GSC直流电压外环模式和锁相环(phase-locked loop，PLL)模式。表2中列出了对图2所示的各类振荡模式参与度较高的主要状态变量。

然后，对图6中的振荡模式进行模态分析。

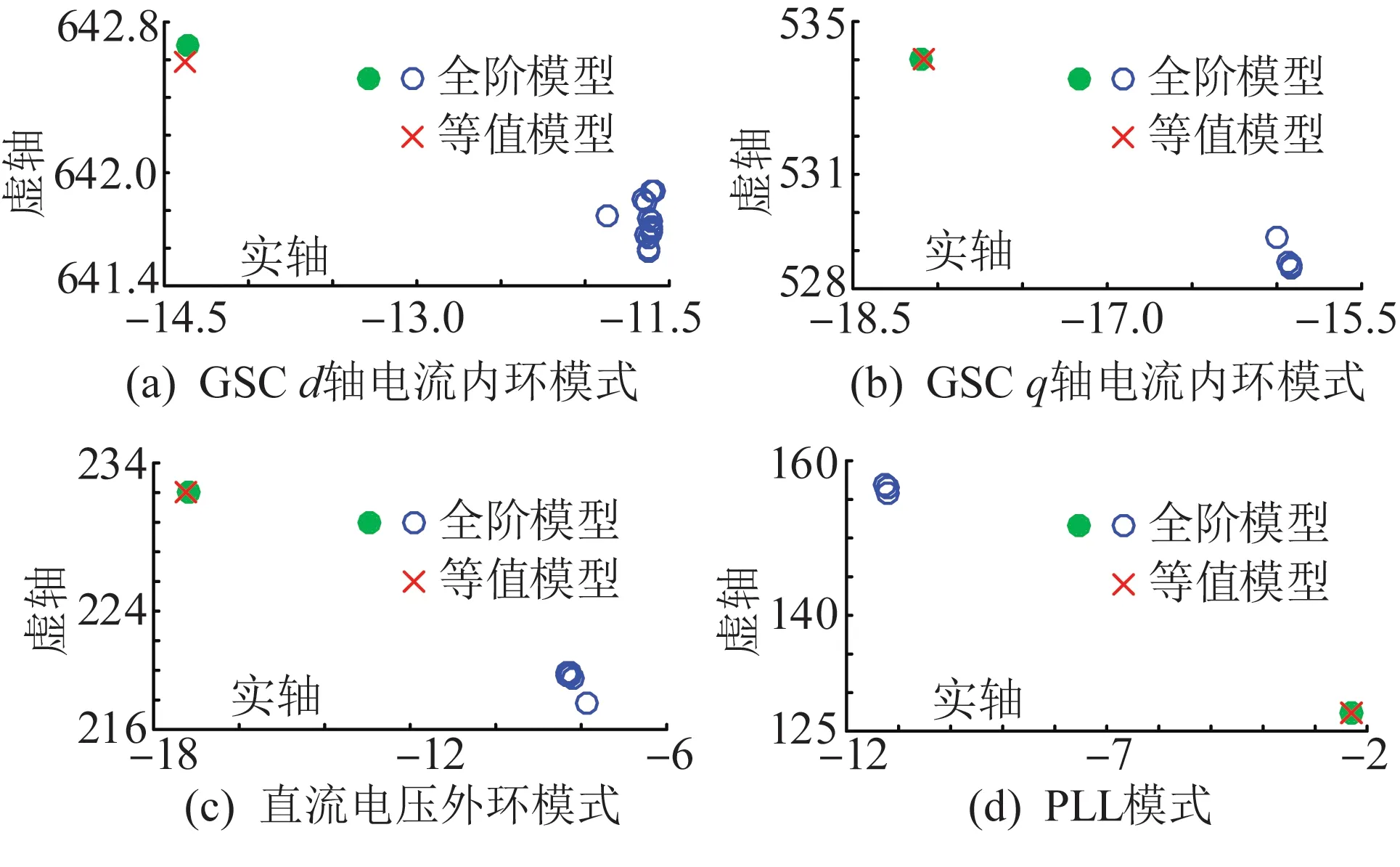
图6 风电场振荡模式计算结果Fig.6 Computational results of oscillations modes of the wind farm

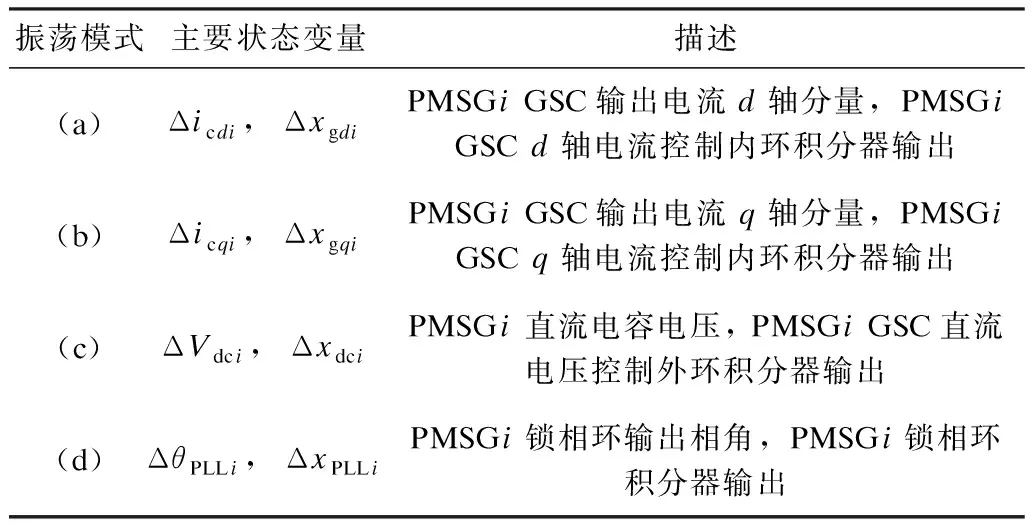
表2 振荡模式高参与度状态变量Tab.2 High participation state variables of the oscillation modes

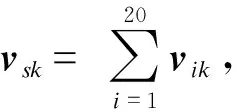
从表3可以看出，图6中圆圈对应振荡模式被激发时，风电场整体活跃程度很小，即这些振荡模式对风电场整体动态输出特性影响较小，本文中称其为风电场内部振荡模式；仅实心圆对应振荡模式决定风电场整体动态输出特性，本文中称其为风电场外部振荡模式。对于实心圆对应的振荡模式，作进一步分析如下。

表3 风电场整体活跃度指标(图6)Tab.3 Activity indexes of the whole wind farm (Fig.6)

以图6(c)中的直流电压外环模式和图6(d)中的PLL模式为例，画出实心圆表示的振荡模式主要状态变量对应模态的实部和虚部如图7所示。可以看出，当实心圆对应振荡模式被激发时，各PMSG对外部电力系统表现出基本一致的动态特性。由于空间限制，此处仅列出图6(c)—(d)中振荡模式的模态，对于GSCd轴和q轴电流内环模式，所得结果情况类似。

图7 风电场振荡模式模态图(图6)Fig.7 Mode shapes of oscillation modes of the wind farm (Fig.6)

最后，对算例风电场采用图4所示单机等值表示形式进行非线性仿真。仿真中的扰动设置为：0.5 s时节点5的有功负荷增加10%，并于0.1 s内恢复，所得结果如图8所示。可以看出，采用等值模型和全阶模型所得非线性仿真结果基本一致，即风电场整体动态输出特性可由1台WTG反映。

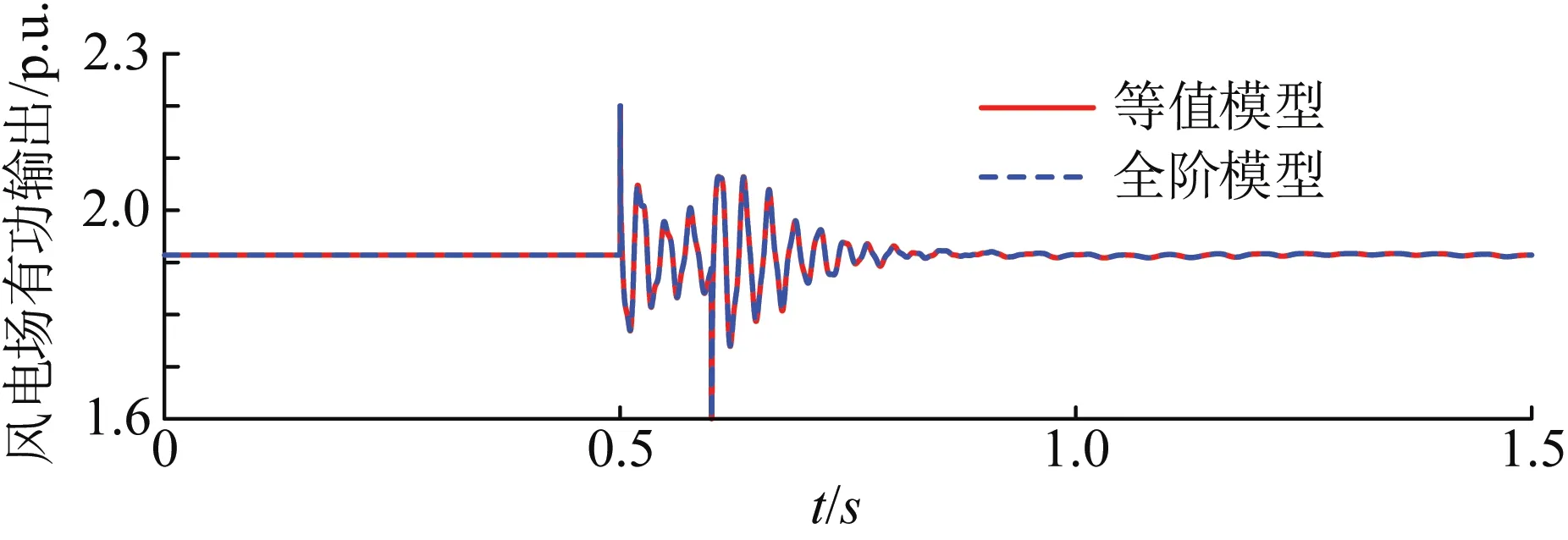
图8 非线性仿真结果(算例1)Fig.8 Non-linear simulation results (study case 1)

3.2 算例2

本小节将附录B图B1所示的风电场分为两个风电机群：风电机群A(PMSG1-PMSG10)和风电机群B(PMSG11-PMSG20)。其中，风电机群A内PMSG运行和参数设定同算例1；风电机群B中PMSG采用另一种参数设定，具体见附录B表B2，且PMSG11有功输出0.15 p.u.，功率因数0.98，其余PMSG功率输出在此基础上随机变化，最大变化范围为±10%。以上场景中风电场可看作是由两种不同型号(不同参数设定、不同额定容量)的PMSG构成，此时，对于风电场而言，条件a不再成立；但是各风电机群内部PMSG参数设定相同且运行点相似，可以满足条件a。

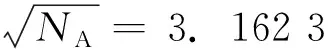
表4 风电机群A连接电抗矩阵特征值特征向量计算结果Tab.4 Eigenvalues and eigenvectors of the network reactance matrix of group A

首先，采用风电场全阶模型，对算例系统进行模式分析，得到风电场直流电压外环模式和PLL模式在复平面上的分布如图9所示。由于空间限制，仅列出直流电压外环模式和PLL模式的计算结果。

然后，依次计算图9(a)—(d)中各振荡模式被激发时，对应风电机群整体活跃度指标，所得结果如表5所示，表中加粗的数值与图9中实心圆表示的振荡模式对应。

从表5可以看出，图9中圆圈对应风电机群内部振荡模式，实心圆对应外部振荡模式。对实心圆对应的振荡模式，以PLL模式为例，给出其主要状态变量对应模态的实部和虚部如图10所示。可以看出，当该振荡模式被激发时，对应风电机群内各PMSG对外部电力系统表现出基本一致的动态特性。

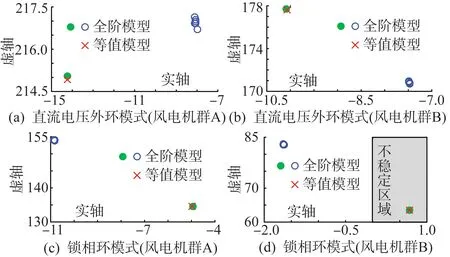
图9 风电机群振荡模式计算结果(算例2)Fig.9 Computational results of oscillation modes of groups of WTGs (study case 2)

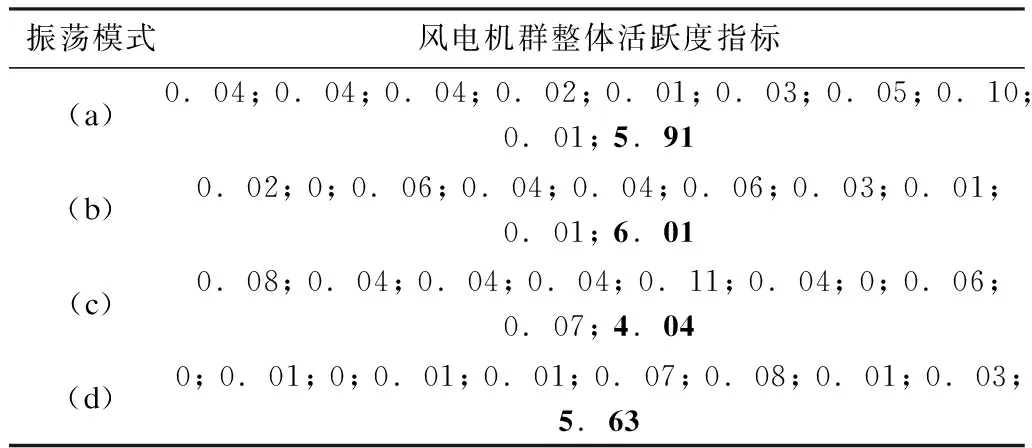
表5 风电机群整体活跃度指标(图9)Tab.5 Activity indexes of the groups of WTGs (Fig.9)

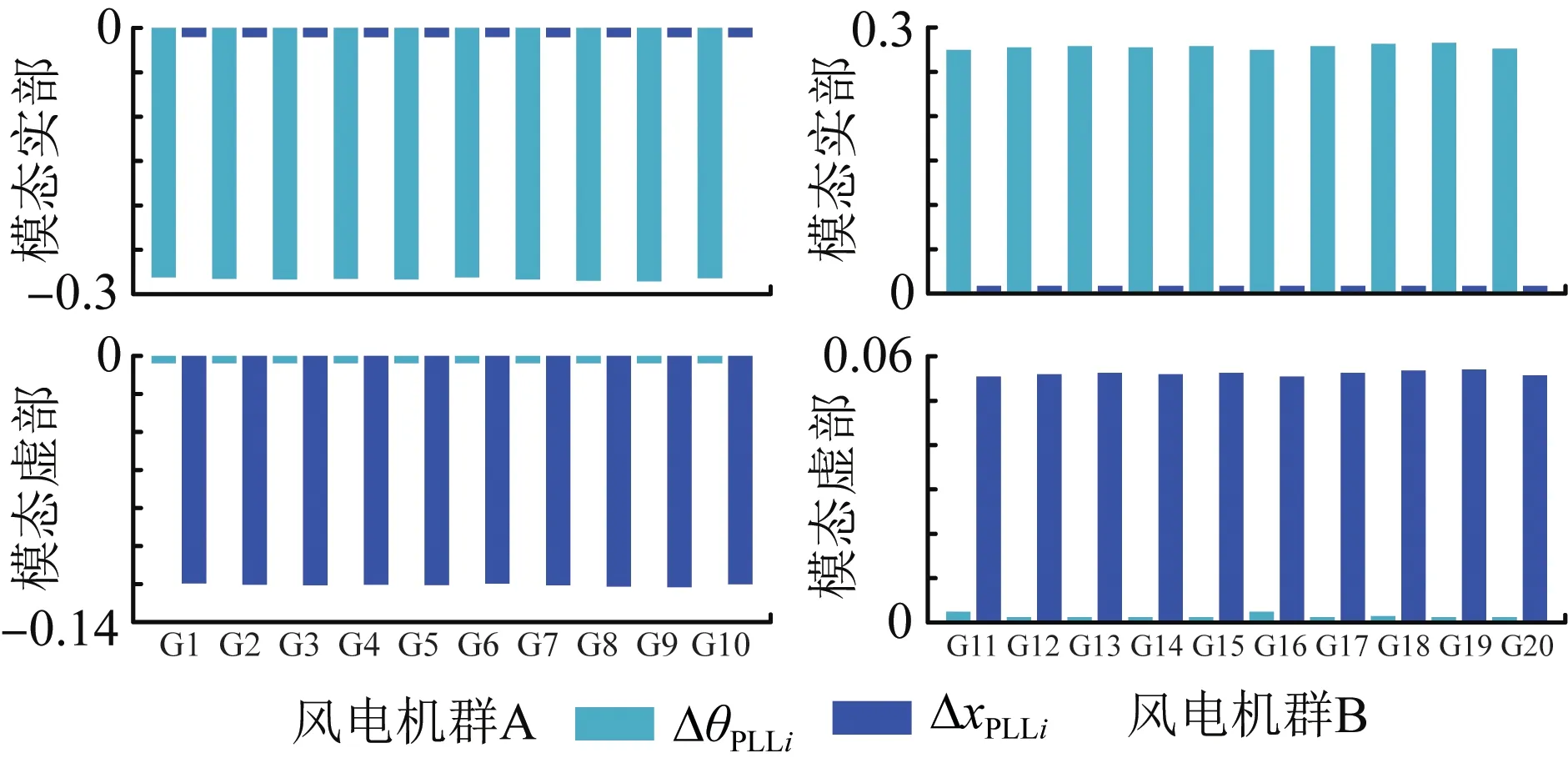
图10 风电机群振荡模式模态图(图9 PLL模式)Fig.10 Mode shapes of oscillation modes of groups of WTGs(Fig.9 PLL modes)

最后，依次建立风电机群A和风电机群B的单机等值模型，并对算例系统进行模式分析，得到风电场振荡模式在复平面上的分布如图9所示。非线性仿真验证结果如图11所示，仿真中的扰动设置为：0.5 s时SG1输入的机械功率降低5%，并于0.1 s内恢复。由图9和图11，采用等值模型和全阶模型所得结果基本一致，验证了满足条件a和条件b时，风电机群整体动态特性可通过一台WTG反映。

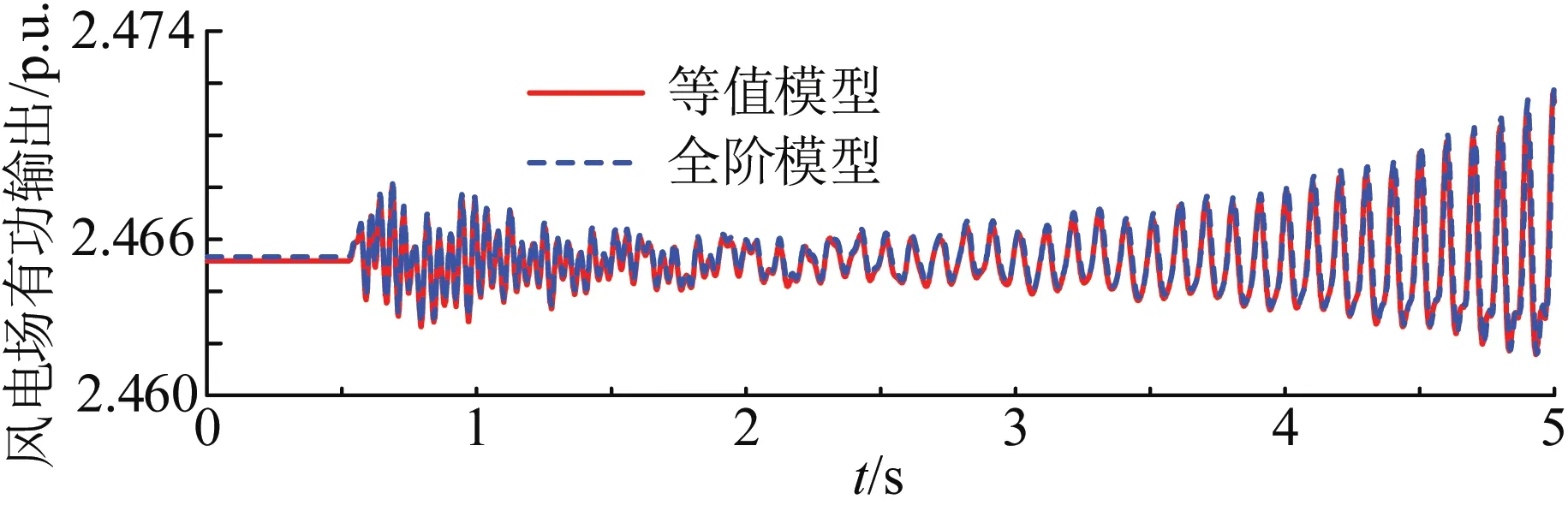
图11 非线性仿真结果(算例2)Fig.11 Non-linear simulation results (study case 2)

3.3 算例3

本算例中，风电场结构以及运行和参数设定同算例1。但是，将风电机群B至母线A的连接线路阻抗ZL2由初始状态下的0.01+j0.1调整至0.04+ j0.4。首先，建立风电场连接电抗矩阵Xw， 计算可得λi、ui和u20如表6所示(i=1,2,…,20)，加粗的数值为λ20和u20；可以看出，由于风电场网络结构的变化，条件b不再成立。

表6 风电场连接电抗矩阵特征值特征向量计算结果2Tab.6 Eigenvalues and eigenvectors of the network reactance matrix of the wind farm 2

然后，建立风电机群B的连接电抗矩阵Xw， 计算可得λi、ui和u10如表7所示(i=1,2,…,10)。可以看出，风电机群B满足条件b。对于风电机群A，其网络结构和参数同算例2，因此也满足条件b。

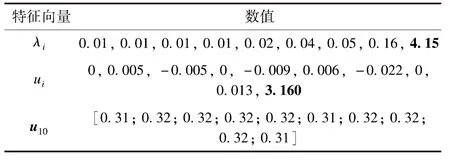
表7 风电机群B连接电抗矩阵特征值特征向量计算结果Tab.7 Eigenvalues and eigenvectors of the network reactance matrix of group B

此外，各风电机群内PMSG参数设定相同、运行点相似，因此，风电机群A和B均满足条件a。

首先，采用风电场全阶模型对算例系统进行模式分析，得到风电场直流电压外环模式和PLL模式在复平面上的分布如图12所示，图中A和B分别代表风电机群A和风电机群B的振荡模式。

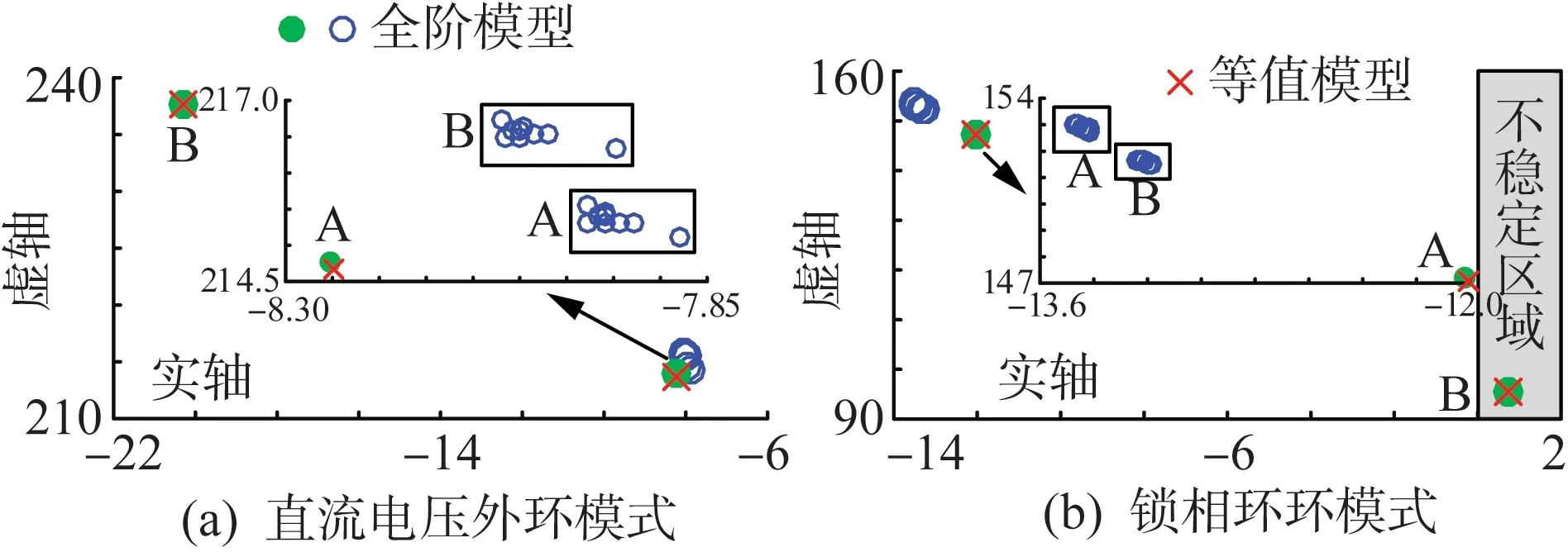
图12 风电机群振荡模式计算结果(算例3)Fig.12 Computational results of oscillation modes of groups of WTGs (study case 3)

然后，计算图12(a)和(b)中各振荡模式被激发时，对应风电机群整体活跃度指标，所得结果如表8所示，其中加粗的数值与图中实心圆表示的振荡模式对应。

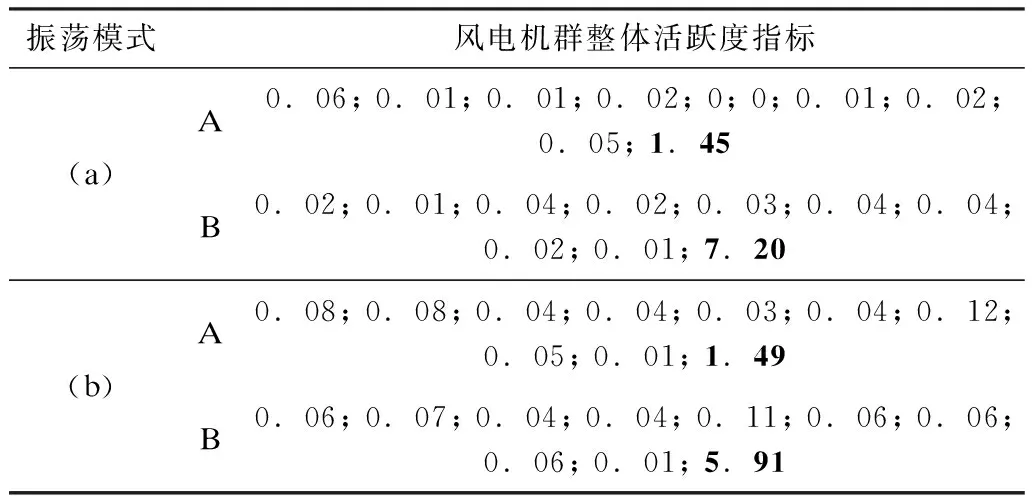
表8 风电机群整体活跃度指标(图12)Tab.8 Activity indexes of the groups of WTGs (Fig.12)

从表8可以看出，图12中圆圈对应风电机群内部振荡模式，实心圆对应外部振荡模式。以PLL模式为例，实心圆对应振荡模式中主要状态变量对应的模态如图13所示。可以看出，振荡模式被激发时，风电机群内PMSG对外表现出基本一致的动态特性。

图13 风电机群振荡模式模态图(图12 PLL模式)Fig.13 Mode shapes of oscillation modes of groups of WTGs (Fig.12 PLL modes)

最后，对风电机群A和风电机群B采用单机等值模型，并对算例系统进行模式分析，得到风电场振荡模式在复平面上的分布如图12所示。非线性仿真验证结果如图14所示，仿真中的扰动设置同算例2。图12和图14进一步表明：满足条件a和条件b时，风电机群整体动态特性可通过1台WTG反映。

图14 非线性仿真结果(算例3)Fig.14 Non-linear simulation results (study case 3)

3.4 算例4

本算例参照某具体海上风电场结构，构建1个大型风电场，对此前所得等值表示形式在风电场规划阶段的应用作具体介绍。海上风电场内，WTG通常按照一定次序规律排列，并通过电缆串并联连接，具体结构见附录B图B2。风电场内PMSG型号相同，额定容量为0.1 p.u.。

首先，建立风电场单机等值表示形式并进行模式计算，得到PLL模式在复平面上的分布如图15所示。

然后，作为对比验证，建立风电场全阶模型并进行模式分析，得到PLL模式在复平面上的分布如图15所示。

最后，分别采用图4所示单机等值表示形式与全阶模型，进行非线性仿真，所得结果如图16所示。

由图15—16可以看出，等值模型有效反映了原风电场的小干扰稳定特性，可用于在风电场规划阶段检验风电场在额定运行状态下的小干扰稳定性。

图15 风电场振荡模式计算结果(算例4)Fig.15 Computational results of oscillation modes of the wind farm (study case 4)

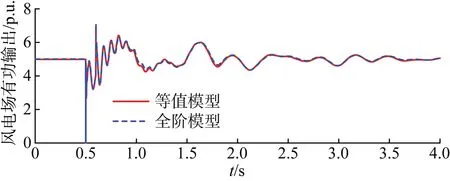
图16 非线性仿真结果(算例4)Fig.16 Non-linear simulation results (study case 4)

4 结论

基于小信号模型，解释了风电机群内的WTG可对外表现出一致的动态特性、且风电机群整体动态输出特性可由1台WTG反映的原因和成立条件。

1)在风电机群内各WTG线性化模型近似相同的条件下，类比模式分析中模式分解的思路，推导了风电机群线性化模型的等效解耦，将N台WTG构成的风电机群解耦为N个由1台WTG并网构成的等效子系统。

2)结合模式分析中模态、可控性和可观性的概念，探讨了风电场同调等值的理论依据，并给出了外部扰动作用下，风电机群内各WTG对外表现的动态特性具有一致性、且整体动态输出特性可由一台等值WTG反映的条件。

3)根据理论推导结果，得到了一种风电机群单机等值表示形式，可用于风电场规划进行小干扰稳定性检验。