四筒导管架基础在砂土中的抗扭承载特性

乐丛欢， 庞雅博， 张浦阳， 丁红岩,3

(1.天津大学 水利工程仿真与安全国家重点实验室， 天津 300350； 2.天津大学 建筑工程学院， 天津 300350； 3.滨海土木工程结构与安全教育部重点实验室(天津大学)， 天津 300350)

近海基础形式多采用固定式结构，主要包括单桩基础、导管架基础、重力式基础、高桩承台基础和筒型基础等。其中筒型基础具有施工快捷和承载力高的优点[1]，导管架基础具有结构刚度大的优势[2]。多筒导管架基础基于筒型基础和导管架基础的优势，针对水深较深的海域(30～50 m)提出的一种基础型式，可用于海洋平台基础、海上风电基础、系泊基础等，具有较好的应用前景[3]。随着深远海风电的开发和风机容量的增大(10 MW甚至更大)，基础所承受的扭矩荷载也在不断增大，其对多筒导管架基础水平和抗弯承载特性的影响也逐渐增大，有必要开展扭矩特性的相关研究。

多筒导管架基础在海洋环境荷载作用下，受力复杂，针对三筒型导管架基础竖向、水平和弯矩的承载力特性已经开展了系统的研究[4-10]。针对扭矩荷载作用下的筒型基础承载特性，武科等[11]通过对软粘土中单筒筒型基础的有限元计算，研究了筒型基础在纯扭矩荷载作用下的破坏特征，并提出了相应的抗扭承载力公式；Zhang等[12]基于层状地基，研究了筒裙高度、筒土摩擦系数以及筒径对复合筒型基础抗扭承载特性的影响，得出了扭矩荷载作用下筒型基础内侧土体对筒壁的作用大于外侧土体的结论，并利用有限元软件，采用固定位移比加载法得到H-T和V-H-T的承载力包络曲线，得出筒型基础扭矩承载力随水平力的增大而缓慢减小，当水平力增大到一定值时，扭矩值明显减小，而竖向荷载对扭矩荷载影响较小的结论；Zhan等[13]通过位移控制法对饱和粘土中筒型基础在扭矩荷载作用下的承载能力进行了研究，并绘制了基础竖向、水平和扭矩荷载各自组合的破坏包络线，得到了扭矩荷载对竖向承载力影响较大，对水平承载力影响较小的结论；范庆来等[14-15]采用荷载-位移联合搜索方法，利用有限元软件对筒型基础在包含扭矩荷载的非共面复合加载作用下的稳定性进行了计算分析，得出了非共面复合加载情况下筒型基础包络面形状不依赖于基础埋深比，可用简单的圆或椭圆方程进行描述的结论，同时提出了包含扭矩的六自由度破坏包络面方程，并给出了方程中偏心度参数取值的确定方法。

目前关于多筒基础在扭矩荷载作用下的承载特性研究较少。本文采用有限元数值模拟方法，对砂土地基中四筒导管架基础在纯扭矩荷载作用下的承载能力进行研究，并进一步分析筒裙高度和筒间距对基础抗扭承载特性的影响。

1 有限元模型

1.1 计算模型

采用ABAQUS有限元软件建立四筒导管架基础的三维有限元模型，如图1所示，其中D、L和S分别代表各个筒体的筒径、筒裙高度和2个相邻筒体之间的距离(简称筒间距)。有限元计算中的地基土体为砂土，采用Mohr-Coulomb本构模型，其参数设置为：密度ρ=2.2 g/cm3，内摩擦角Ψ=34.46°，粘聚力c=3.27 kPa，压缩模量Es=18 MPa，泊松比μ=0.3。为了消除边界条件对四筒导管架基础承载性能的影响，地基土体采用长×宽×高为200 m×200 m×80 m的立方体，土体底面为全固定约束，侧面施加水平约束，土体和基础之间采用接触对模拟。

图1 有限元计算模型Fig.1 Finite element model

1.2 加载方式

采用位移控制法来实现基础上外荷载的施加，即在加载控制点上施加某方向的位移，直至基础处于极限状态。所施加荷载的正向规定如图2所示，其中T代表扭矩荷载，对应位移为θ。

图2 正向荷载规定Fig.2 Positive loading direction

1.3 计算方案

计算方案如表1所示。表中B0方案为基础方案，其他方案均在基础方案上改变相关参数。如表1中所示，L1、L2、L3和L4为L系列方案，变量只有筒裙高度L，依此类推，S系列方案变量为筒间距S。

1.4 模型验证

为验证有限元计算结果，开展了物理模型试验。模型试验(比尺1∶100)在长×宽×高为2 m×2 m×1.5 m的砂土土槽中展开，土体主要参数与计算模型一致。试验主要针对0°、22.5°、45°这3个角度进行不同角度的水平承载力加载试验，其中外力的加载通过推杆作用于模型上部的加载片实现，试验装置如图3所示，物理模型试验现场如图4所示。

表1 计算方案Table 1 Calculation scheme

图3 试验加载测量简图Fig.3 Diagram of loading measuring device

在有限元计算中，采用与试验相同的结构尺寸和土体参数建立有限元模型。图5给出了有限元与试验的对比结果，二者的整体趋势相似，有限元结果与模型试验结果吻合较好，对于3组不同加载角度下的水平极限承载力，二者最大误差为8.3%，平均误差为4.8%，验证了有限元模拟结果合理性。

2 承载力标准

本文采用Villalobos[16]描述的极限承载力确定方法：如图6所示，在曲线弹性阶段起点和塑性阶段终点处分别作切线，2条切线相交于一点，然后从交点出发画一条水平直线与曲线相交，将水平直线与曲线的交点定义为基础的极限状态，其对应的荷载为相应的承载力，如图中圆点所示。为方便研究基础的承载特性，对基础筒体和筒体上研究路径进行编号，如图7所示。其中路径1～4位于筒壁上沿-Z方向。

图4 模型试验Fig.4 Model test

图5 试验与有限元结果对比Fig.5 Comparison of test and finite element results

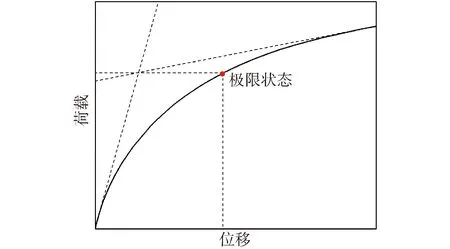
图6 极限承载力确定标准Fig.6 Determination standard of ultimate bearing capacity

3 四筒导管架基础的抗扭承载特性

在扭矩荷载作用下，四筒导管架基础围绕中心轴线发生扭转运动，4个筒体的筒壁由于扭转与周围土体相互作用产生的土压力分布具有较强的规律性，如图8 所示。各个筒体的筒壁土压力分布形态及大小近似相同，但主要分布位置存在顺时针90°的相位差，由于土压力分布的相似性，本节只选取筒A为研究对象。

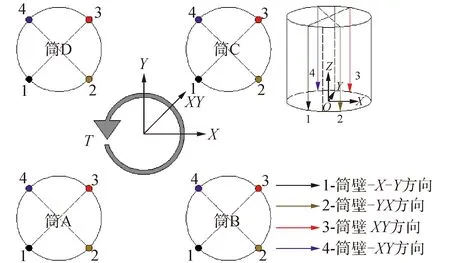
图7 四筒导管架基础筒体编号Fig.7 Number of four-bucket jacket foundation

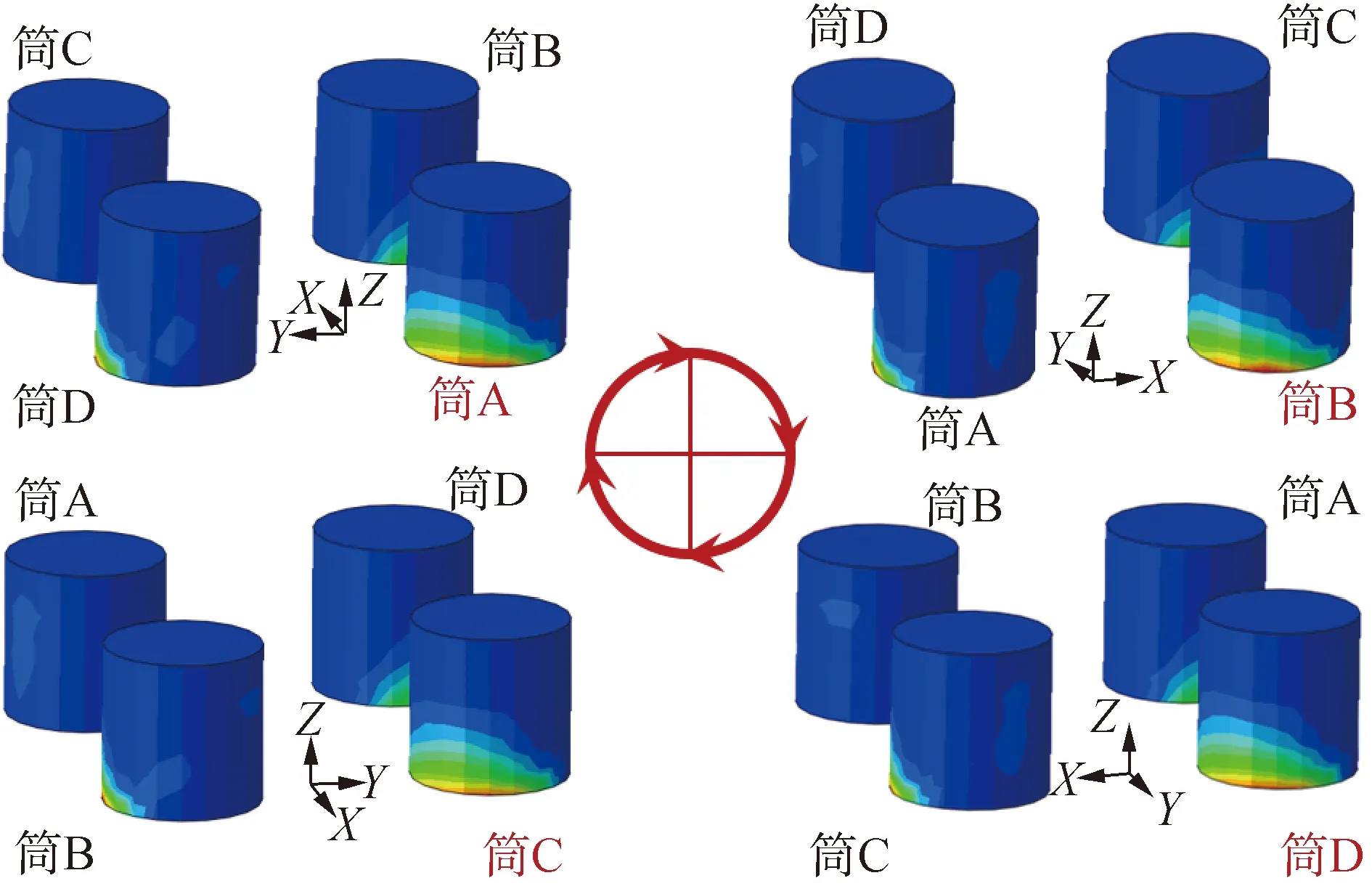
图8 扭矩荷载作用下基础筒壁土压力Fig.8 Soil pressure of the bucket skirt under torque loading

3.1 筒裙高度的影响

图9和图10分别为砂土地基中不同筒裙高度的四筒导管架基础扭矩-转角曲线以及抗扭承载力与筒裙高度的关系曲线。由图可知，四筒导管架基础的抗扭承载能力随着筒裙高度的增加逐渐提高，筒裙高度从9 m增加到21 m，极限承载力数值依次为5 240、6 330、7 410、8 740、9 680 MN·m，二者近似为线性关系，筒裙高度每增加3 m，基础承载能力约提高18%。

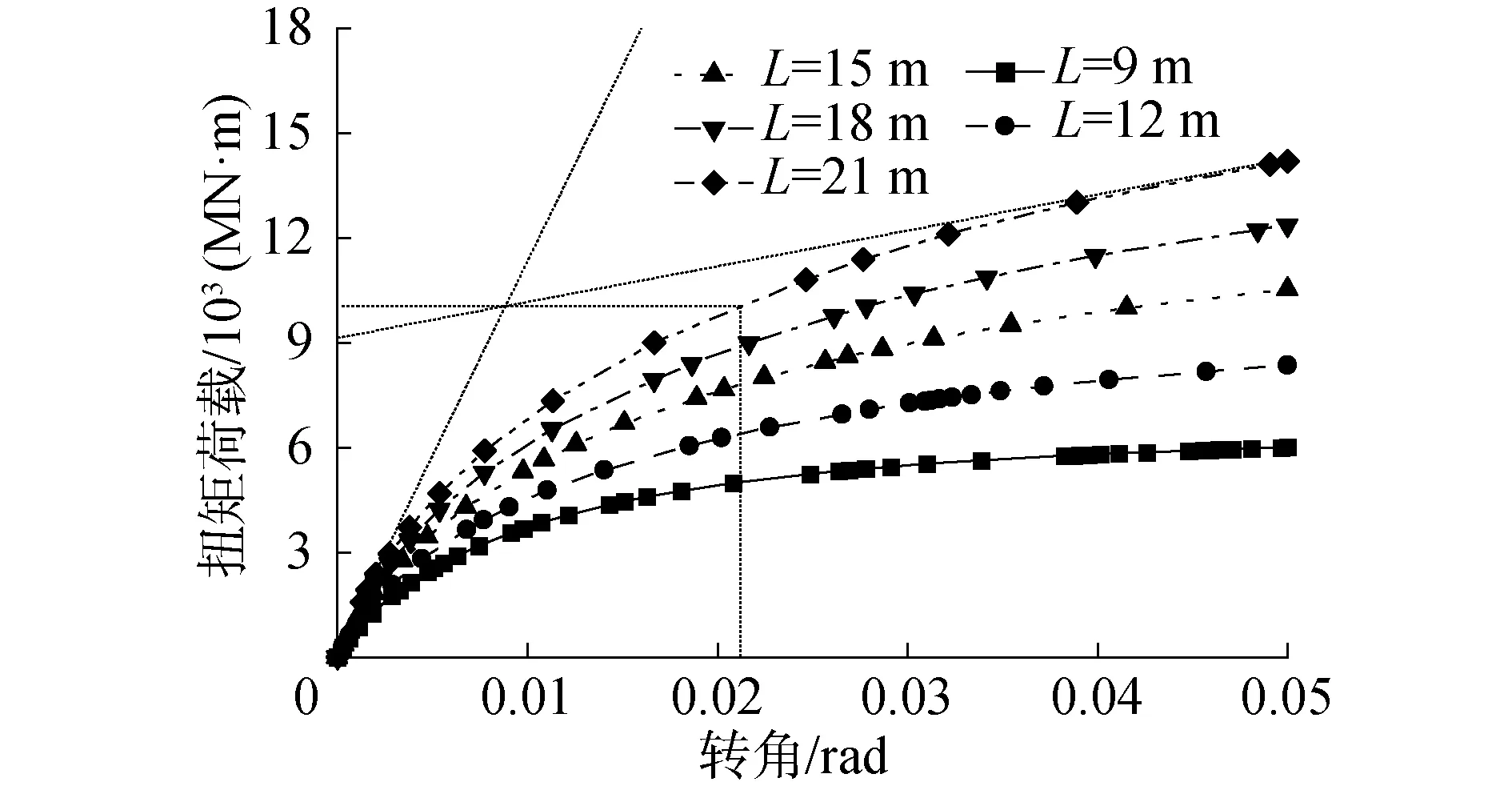
图9 不同筒裙高度基础扭矩-转角曲线Fig.9 Rotation-torque curves under different bucket skirt heights

图10 不同筒裙高度下的基础抗扭承载力Fig.10 Torque-bearing capacities of different bucket skirt heights

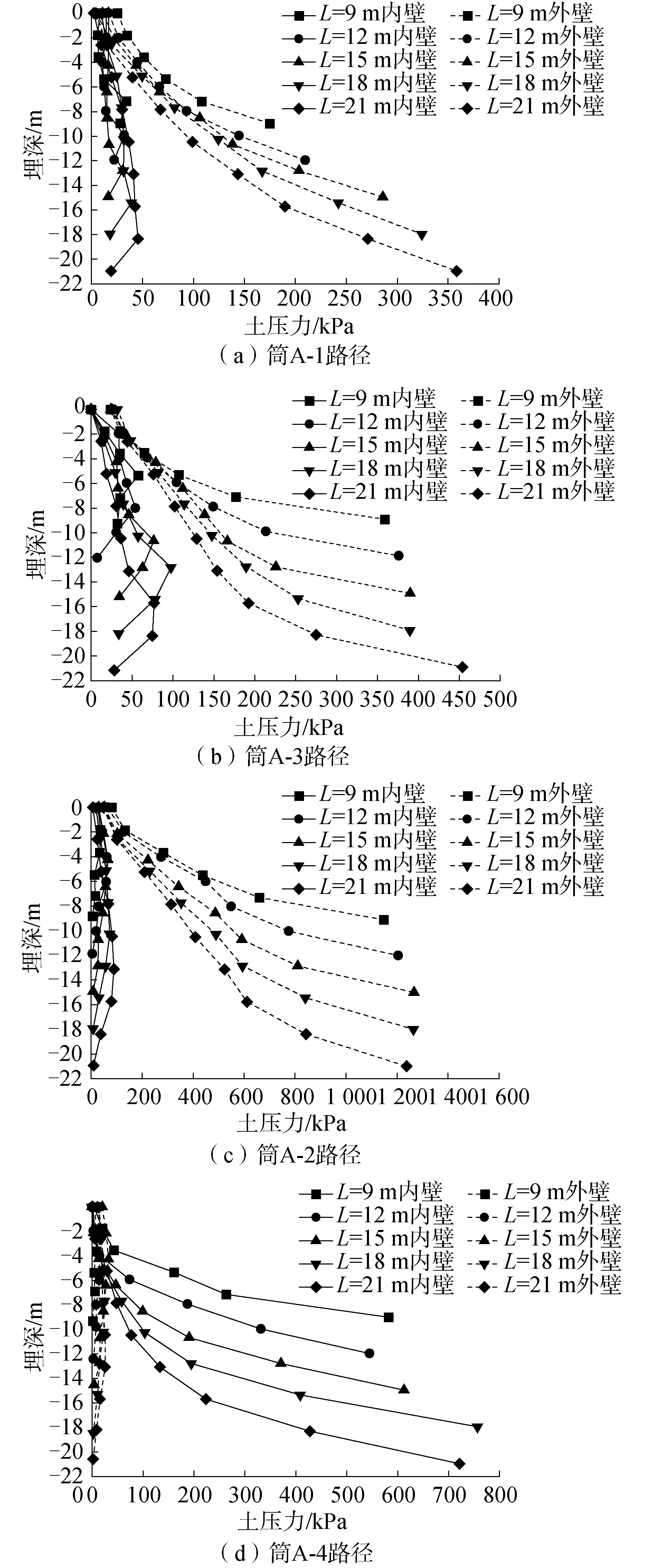
图11 不同筒裙高度基础筒壁土压力分布Fig.11 Soil pressure of skirt under different bucket skirt heights

图11为基础达到抗扭承载能力后筒壁路径1、3和2、4土压力，从图中可以看出，主动土压力随着埋深的增加在小范围内波动后，在筒体底部趋近于0，且基本不随筒裙高度变化。而被动土压力随着埋深的增加呈现明显的增长趋势，且受到筒裙高度的明显影响，各个路径的被动土压力均随着筒裙高度的增加而增大。综合各个路径被动土压力曲线可以看出路径1、2、3均是筒体外侧土体为被动区域，而路径4是筒体内侧为被动区域，且路径2、4的土压力值相对较大，尤其是路径2土压力值最大。图12为筒体底部沿筒周方向的土压力，由图可知，筒体内外土压力均随着筒裙高度的增加而增大，且内外土压力分布呈现直角坐标系二、四象限对角形态，结合图7的筒体路径编号可知，此对角形态与图11中各路径的土压力相对应。综上，可以认为筒裙高度的增加在一定程度上提高了基础的抗扭承载能力，且基础的各个筒体在扭转的同时沿自身的一个对角方向发生倾斜。

图12 不同筒裙高度基础筒底土压力分布Fig.12 Soil pressure of bottom under different bucket heights

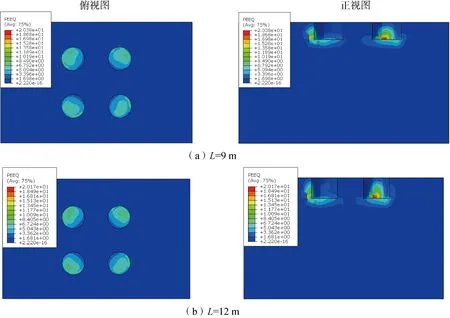
图13为在扭矩荷载作用下不同筒裙高度基础对应的地基等效塑性应变云图，由图可知，不同筒裙高度下的地基等效塑性应变云图呈现统一的规律，与图8的土压力分布规律类似，四筒的土体破坏在形式上为从筒A开始，依次逆时针旋转90°的对角破坏，且随着筒裙高度的增加基础筒壁外侧与底部的等效塑性应变范围逐步扩大，基础的抗扭承载能力逐渐提高。

3.2 筒间距的影响

图14和图15分别为砂土地基中，不同筒间距的四筒导管架基础扭矩-转角曲线以及抗扭承载力与筒间距的关系。由图可知，四筒导管架基础的抗扭承载能力随着筒间距的增加，逐渐提高，筒间距从9 m增加到21 m，极限承载力数值依次为4 820、6 190、7 420、8 970、10 980 MN·m，二者近似为线性关系，筒间距每增加3 m，基础抗扭承载力约提高23%。

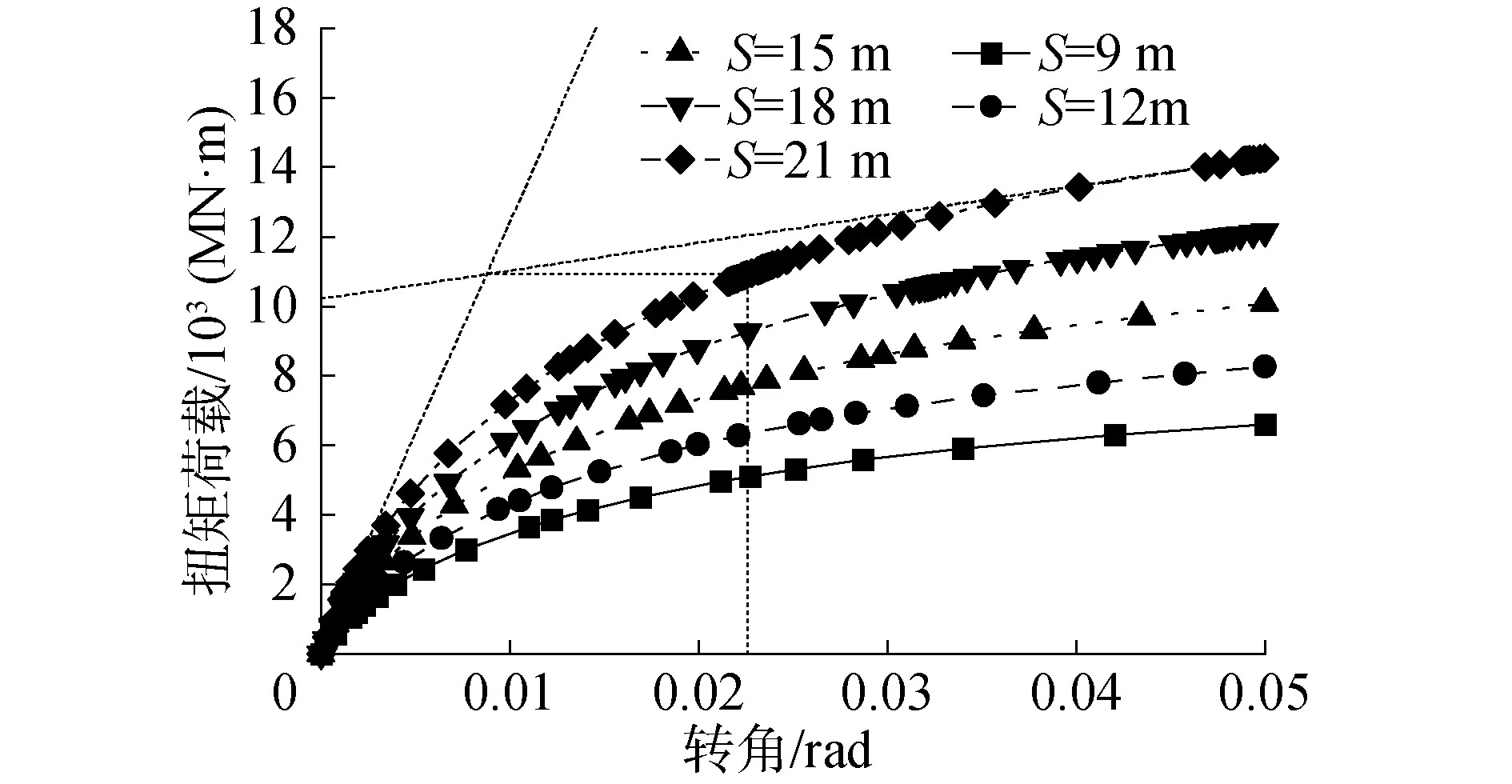
图14 不同筒间距基础扭矩-转角曲线Fig.14 Rotation-torque curves under different bucket spacing

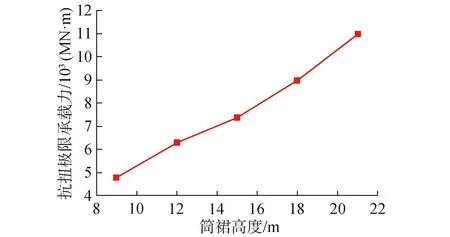
图15 不同筒间距的基础抗扭承载力Fig.15 Torque-bearing capacities under different bucket spacing

图16为基础达到抗扭承载力时筒壁路径1、3和路径2、4土压力，从图中可以看出，路径2、4的主动土压力随着埋深的增加基本没有变化，且不受筒间距的影响，路径1、3在小范围内波动，随筒间距的变化比路径2、4明显，但仍呈现较小的影响。被动土压力仍随着埋深的增加呈现明显的增长趋势，除路径2被动土压力受到筒间距的明显影响以外，其余路径随筒间距的变化均很小，其中路径4基本不受筒间距变化的影响，但因为路径2土压力值是其他路径的2倍左右，所以认为筒间距的增大在一定程度上可以提高基础的抗扭承载能力。

图17为筒体底部沿筒周方向的土压力，由图可知筒体外部土压力随着筒间距的增加而增大，内部土压力无明显变化，且内外土压力分布仍呈现直角坐标系二四象限对角形态，结合图7的筒体路径编号可知，此对角形态与图16中各路径的土压力相对应。

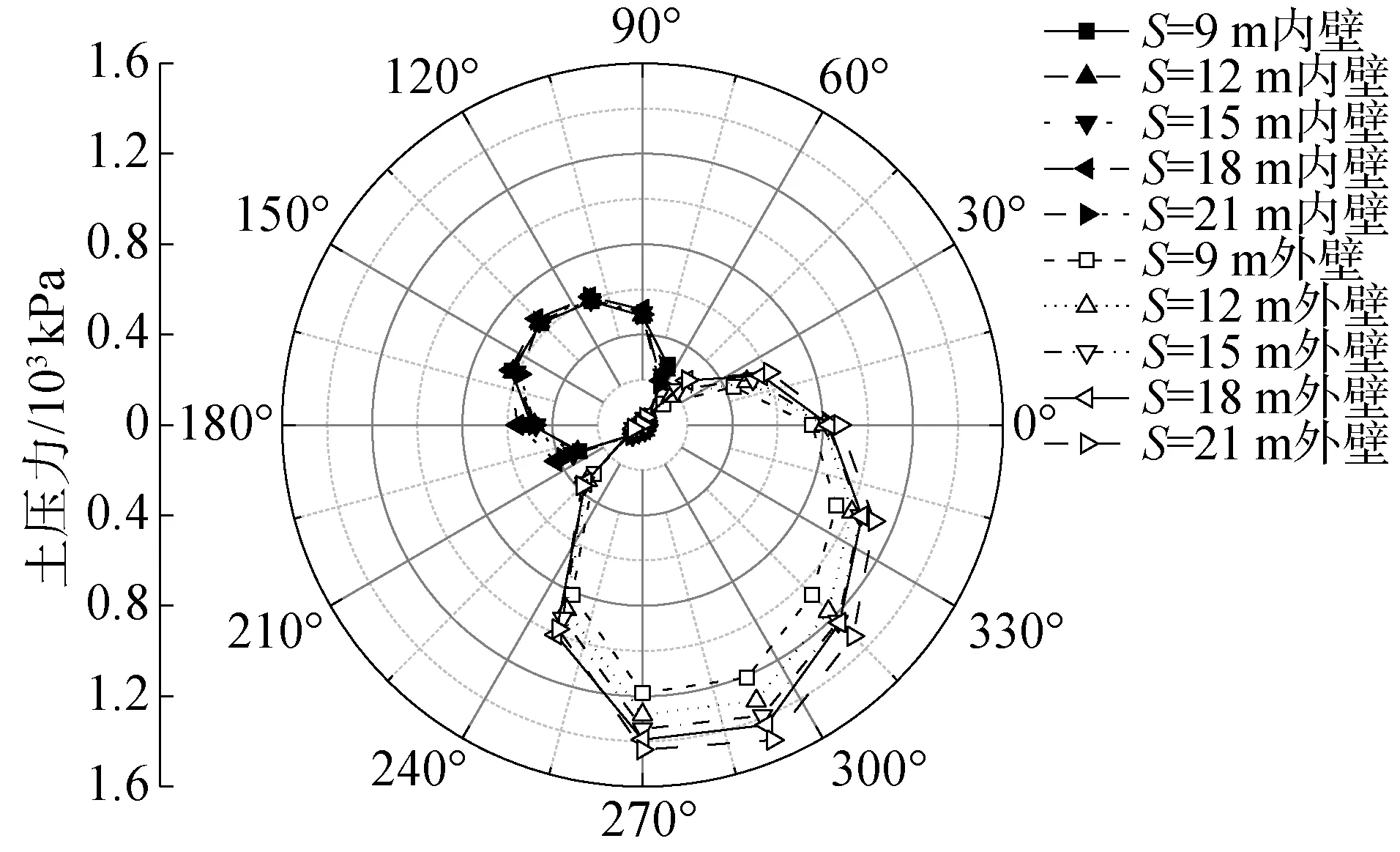
图17 不同筒间距基础筒底土压力分布Fig.17 Soil pressure of bottom under different bucket spacing

图18为在扭矩荷载作用下不同筒间距基础对应的地基等效塑性应变云图，由图可知，当筒间距为9 m时，筒群效应较为明显。随着筒间距的增大，筒群效应不断减弱，当筒间距增大至一定程度后，各筒体之间基本不再存在明显的相互作用，综上可知，筒间距的增大在一定程度上降低了四筒基础的筒群效应，且随着筒间距的增大，等效塑性应变值逐渐增大，基础的抗扭承载能力逐渐提高。

4 结论

1)四筒导管架基础在纯扭矩荷载作用下的土体破坏呈现一种从某一筒体开始，依次逆时针旋转90°的对角破坏，且筒体内外土压力分布也呈现对角形态，各个筒体在扭转的同时沿自身的一个对角方向发生了倾斜。

2)随着筒裙高度的增加，四筒导管架基础达到抗扭承载能力后筒壁埋深方向的主动土压力没有明显变化，而被动土压力明显增大，筒体底部沿筒周方向的筒体内外土压力也呈现增大趋势，并呈现直角坐标系二四象限对角形态分布。同时，基础筒壁外侧与底部的等效塑性应变范围逐步扩大。

3)随着筒间距的增大，四筒导管架基础达到抗扭承载力时筒壁埋深方向的主动土压力没有明显变化，但波动范围略大于筒裙高度，而被动土压力较大的一侧有明显的增长趋势，筒体底部沿筒周方向的筒体外部土压力明显增大，而内部土压力无明显变化，但内外土压力分布仍呈现直角坐标系二四象限对角形态。

4)筒裙高度和筒间距的增加均提高了基础的抗扭承载力，且四筒导管架基础的扭矩极限承载力随着2种变量的增加近似呈线性增长，增长速率也近似相同。