未知荷载系数法在钢箱拱桥缆索吊装中的应用

周里鸣 莫荣华 王正

大跨度钢箱拱桥常采用缆索吊装工艺，施工安装节段多，只有进行详细的施工过程仿真分析，才能使结构线形和受力状态满足设计和规范要求。文章阐述了钢箱拱桥吊装施工过程变形调整方法、扣索力确定原则以及施工中的注意事项，并以梧州市西江四桥为例，采用有限元分析软件Midas Civil进行施工过程模拟分析，利用未知荷载系数法进行索力的优化调整，所得结果与实测结果基本一致。该方法可以得到令人较为满意的设计线形，可广泛应用于类似工程。

有限元;钢箱拱;缆索吊装;未知荷载系数法;扣索索力

文献标识码：U441+.2-A-33-109-5

0 引言

大跨度钢箱拱桥拱肋施工常采用缆索吊装工艺，不同于钢管混凝土拱桥，在施工阶段拱肋拱脚固结，拱肋刚度较大，后期通过扣索力调整拱肋标高难度较大。同时，拱肋划分节段较多，属于高次超静定结构，后期张拉索力又会引起前面已安装阶段的索力变化，整个施工过程对扣索张拉力控制及线形控制具有较高要求。目前常采用的零弯矩法与零位移法要求整个施工过程拱肋均处于设计线形位置，优点在于合龙过程中不需要调整;缺点在于整个施工过程中需要不断放松和张拉扣索力，施工过程具有一定风险，调索较为复杂繁琐，工期较长。本文以梧州市西江四桥主拱肋缆索吊装为例，采用未知荷载系数法，施工过程中考虑后续阶段对前面阶段索力和线形的影响，扣索一次张拉到位，线形控制良好，同时有效缩短了工期。

1 缆索吊装过程中未知荷载系数法应用

1.1 确定扣索索力的原则

（1）缆索吊装过程中采用的扣索应力应小于容许应力，并考虑一定的安全系数。施工过程中常采用钢绞线作为扣索，扣索容许的最大应力为破断力的50%，即须考虑2.0的安全系数。

（2）扣索索力最大值的选取。整个施工过程中扣索力一直处于变化过程中，在进行所有吊装施工节段分析后，确定每段扣索的最不利索力，依次进行配索。

（3）扣索索力在整个施工过程中不应有较大的变化，以免引起扣索几何非线性影响的增加。

（4）扣索索力的整个过程控制，应使拆除扣索后，拱肋线形与一次落架成拱线形接近。

1.2 钢箱拱桥切线拼装偏差分析

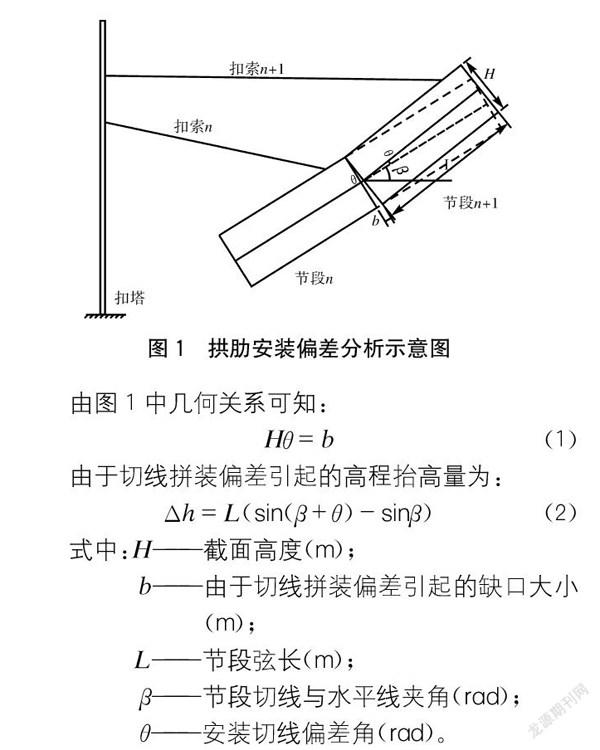
拱肋标高的调整包含两个部分：（1）施加扣索力來调整标高;（2）施工过程中适当调整切线拼装角来调整标高。施工过程中，在满足焊接工艺的条件下，可以通过调整拱肋节段的切线拼装角，实现拱肋无应力状态的线形调整。但其调整量不应太大，否则会造成拱肋节段间焊接困难。构件切线拼装偏差分析见图1。

由图1中几何关系可知：

Hθ=b（1）

由于切线拼装偏差引起的高程抬高量为：

Δh=L（sin（β+θ）-sinβ）（2）

式中：H——截面高度（m）;

b——由于切线拼装偏差引起的缺口大小（m）;

L——节段弦长（m）;

β——节段切线与水平线夹角（rad）;

θ——安装切线偏差角（rad）。

1.3 整个施工过程中应注意的其他问题

（1）温度影响。钢结构对温度影响比较敏感，整个施工过程要做好温度监测，并做好温度影响下的结构变形、结构内力分析。

（2）扣塔偏位影响。扣塔偏位对拱肋的标高有较大影响，施工过程中要保证扣塔水平偏位在允许范围内，一般为10 mm。

（3）张拉扣索时间问题。拱肋安装一般分为吊装定位、码板焊接、拱肋焊接、张拉扣索（同步减少缆索吊装索力）等步骤，施工过程应避免将拱肋焊接与扣索张拉同步进行，以免引起焊缝开裂，影响结构安全。

1.4 未知荷载系数法介绍

未知荷载系数法，是指结构在线弹性条件下，对要求的未知量给一组任意初始值（一般为1），然后给定结构的约束条件，可为内力、变形等，经过迭代计算得到满足约束条件的最优解。一般用未知荷载系数法求解缆索吊装索力的方程如下：

LV≤δ11T1+δ21T2+δ31T3+δ41T4+δ51T5+δ61T6≤UV

LV≤δ22T2+δ32T3+δ42T4+δ52T5+δ62T6≤UV

LV≤δ33T3+δ43T4+δ53T5+δ63T6≤UV

LV≤δ44T4+δ54T5+δ64T6≤UV

LV≤δ55T5+δ66T6≤UV

LV≤δ66T6≤UV（3）

式中：δij——为索力Ti作用引起的节点j的竖向位移（mm）;

UV——约束条件的上限;

LV——约束条件的下限。

由于上式为不等式解，会存在多组解，一般采用最小二乘法得到优化索力解。

1.5 扣索索力求解流程（图2）

2 工程实例

2.1 桥梁概况

梧州市西江四桥主桥为钢箱系杆拱桥，由300 m中跨和两侧对称布置的129 m边跨组成。主桥全长为558 m。拱肋桥面以下采用变截面混凝土结构，桥面以上均采用变高钢箱截面。其中主跨和边跨均采用缆索吊装施工，主跨分15节段吊装施工。主跨缆索吊装施工工序如下：缆索起重机安装、两岸第1段拱肋吊装→安装扣索→接头焊缝→拱肋标高调整→两岸第2段拱肋吊装→码板临时连接→安装扣索→接头焊缝→第二段拱肋标高调整→直至两岸第15段安装完毕→合龙段安装。

2.2 有限元模型分析

采用Midas Civil软件建立结构有限元模型，拱肋、塔架等采用梁单元模拟，拉索、系杆、吊杆等采用桁架单元模拟，边界条件根据实际情况模拟（见图3）。

2.3 索力与预抬量计算结果

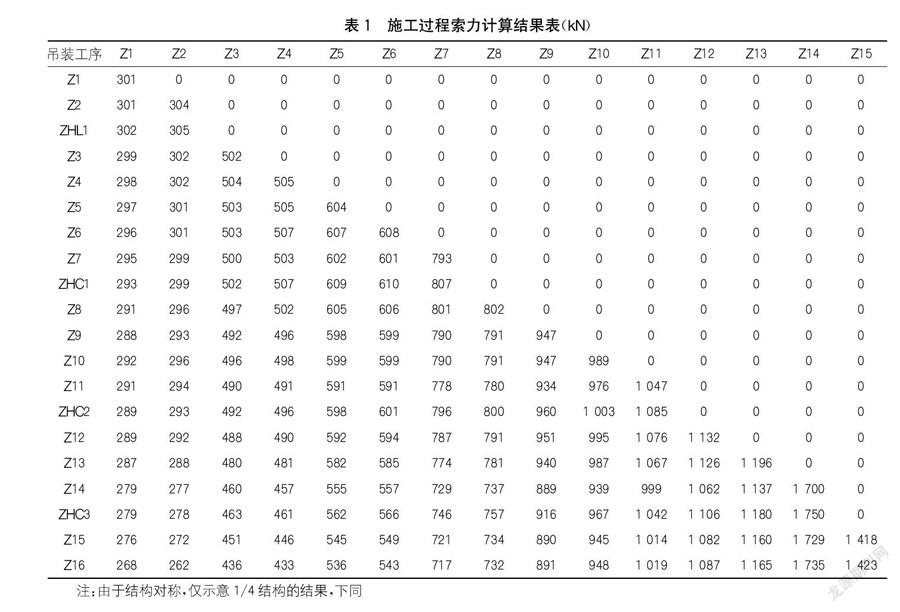
本桥缆索吊装计算采用正装分析方法。以主拱吊装为例，在预应力混凝土拱肋节段上，依次按照顺序安装Z1～Z15节段，最后吊装Z16合龙段。给定扣索索力初始值为1，采用未知荷载系数法，以拱肋测点变位为约束条件，计算出满意的索力。同时，将成拱节段的变形值反向作为施工过程中的预抬量，整个施工过程中拱肋最大预抬量为30.1 mm。拱肋立模安装基本维持在制造线形附近，线形测点位于距拱肋节段接头1 m位置处。索力计算结果见表1，预抬量计算结果见表2。

2.4 计算索力变化量分析

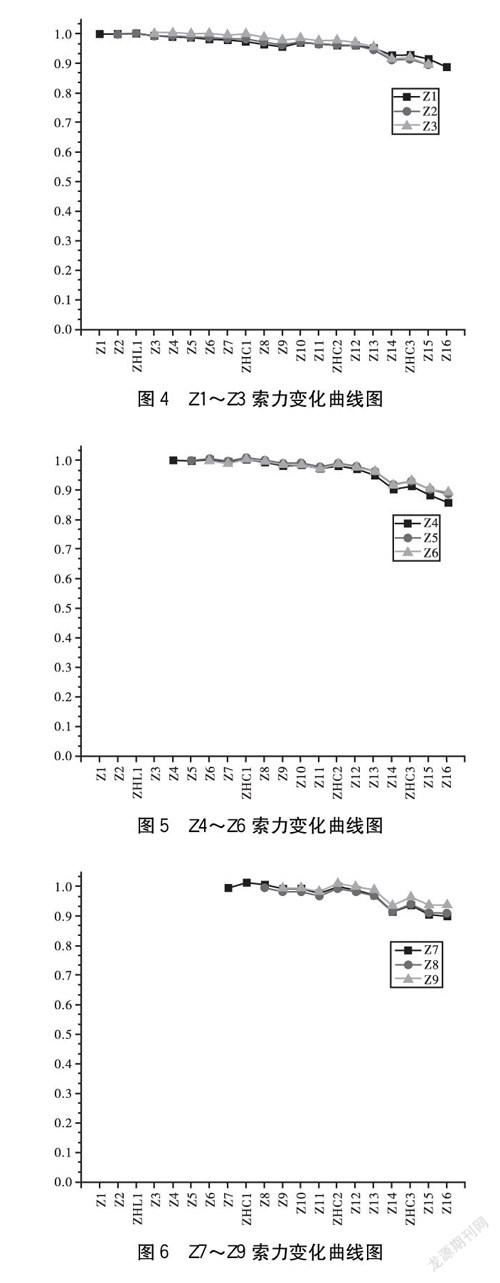
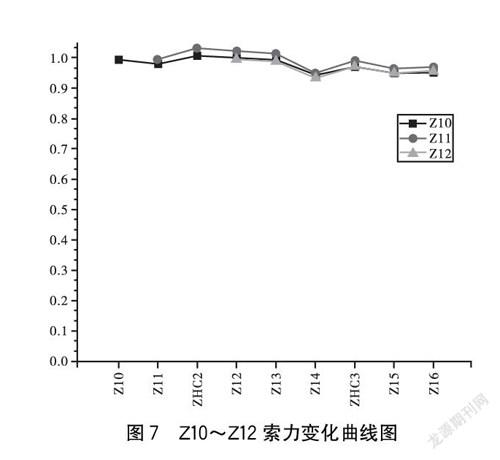
在施工过程中，后续节段的安装会对之前安装节段的索力和变形产生影响，如果这种影响较大，将会使索力出现比较大的垂度，与线弹性理论计算结果存在较大出入，影响施工控制精度。因此，在施工过程中，调整的索力变化量要尽可能地小一些，这对施工控制是有利的。以吊装当前阶段的初始张拉索力为标准值，计算出不同施工阶段索力的变化量，结果如下页图4～7所示。

由图4～7可见，初始张拉索力总体呈下降趋势。在吊装合龙阶段，Z1～Z6号索索力有较明显的下降，Z7～Z9号索索力基本持平，Z10～Z12号索索力有所上升。总体来看，施工过程中索力减少量最大在14%左右，索力保持量均在86%以上，不会引起比较大的扣索垂度变化，对施工中的索力控制较为有利。

2.5 索力、变形偏差分析

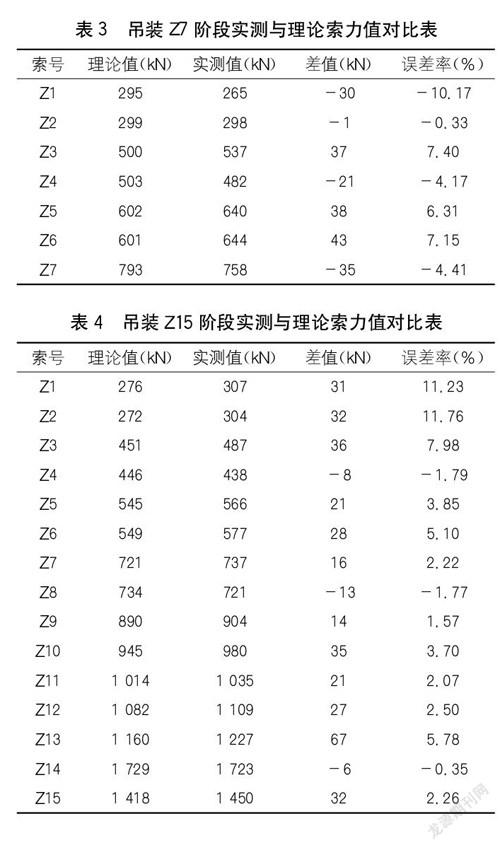
在施工监控过程中，要及时关注缆索吊装过程中索力与变形的变化情况，及时与理论值进行对比，保证整个吊装过程中结构受力安全、线形可控。限于篇幅，仅列出Z7、Z15吊裝阶段的索力、线形对比结果，见表3～6。

由表3、表4测试结果看，吊装Z7阶段，索力差值为-35～43 kN，偏差百分比为-10.17%～7.40%;吊装Z15阶段，索力差值为-13～67 kN，偏差百分比为-1.79%～11.76%。实测索力与计算索力基本一致。

由表5、表6测试结果看，实测变形与理论变形偏差为-5.0～0.9 mm，实测变形与理论变形基本一致。

2.6 成拱线形分析

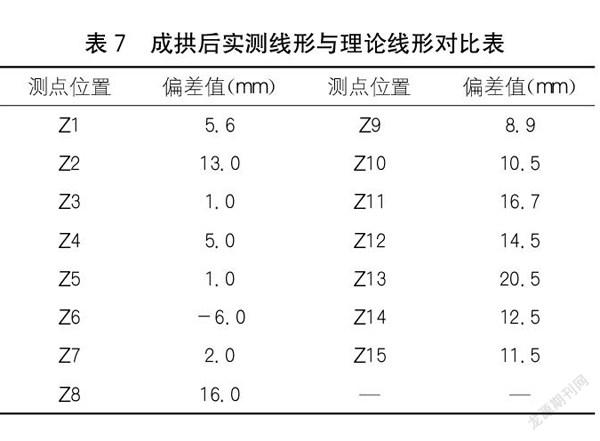
拱肋缆索吊装施工完成后，成拱线形为线形控制的最终成果，实测线形与理论线形偏差值见表7。

由表7可知，实测线形与理论线形偏差为-6.0～20.5 mm，最大偏差值仅20.5 mm，成拱线形与理论线形基本一致，取得了较好的施工控制效果。

3 结语

（1）从线形结果分析：采用未知荷载系数法计算的索力能够较好地满足施工控制的要求，取得良好的控制效果。

（2）从计算的经济性上分析：采用未知荷载系数法可在较短时间内求得满意的索力，避免了建模计算过程中大量的试算工作，提高了工作效率。

（3）从施工便利性来讲，采用未知荷载系数法计算的索力在施工中一次张拉就位，不需要频繁调索，可以有效缩短施工工期。

（4）未知荷载系数法作为一种比较可靠的计算索力的方法，可以更广泛地推广到更多的缆索吊装项目中去。

参考文献

[1]JTG D64-2015，公路钢结构桥梁设计规范[S].

[2]卢佳森.多桅杆斜拉结构的索力确定方法[J].建筑结构，2011（S1）：886-889.

[3]JTG D60-2015，公路桥涵设计通用规范[S].

[4]袁建新.南广铁路西江特大桥钢箱拱肋吊装施工过程仿真分析[J].世界桥梁，2016，44（1）：55-59.

[5]连岳泉，肖建良，王小成.大跨径拱桥拱肋吊装过程索力仿真分析[J].中外公路，2008，28（5）：146-149.

收稿日期：2021-03-22

作者简介：周里鸣（1981—），硕士，高级工程师，主要从事桥梁检测及设计工作;

莫荣华（1986—），高级工程师，主要从事桥梁建设管理工作;

王 正（1991—），硕士，工程师，主要从事桥梁检测及设计工作。