后疫情时代，债券投资的思考

摘 要：近几年，在银行间债券市场中，包商银行事件，天齐锂业、清华紫光、永煤违约主体不断爆出，债券违约事件频发和金融机构负面舆情增多背景下，国债以收益性、安全性和流动性受到越来越多的投资者选择。本文基于ARMA模型对国债收益率进行预测，帮助投资者依据预测结果制定、调整相应的国债交易策略，不断提高规避债券风险能力和提高债券收益率。

关键字： ARMA模型;国债;收益曲线

本文索引：苏蓉.<变量 2>[J].中国商论，2021（23）：-086.

中图分类号：F812.5 文献标识码：A 文章编号：2096-0298（2021）12（a）--04

近几年，在银行间债券市场中，包商银行事件，天齐锂业、清华紫光、永煤等违约主体不断爆出，债券违约事件频发和金融机构负面舆情增多背景下，国债以收益性、安全性和流动性受到越来越多的投资者选择。收益率变动是所有投资者时刻关注的重要交易信息，收益率曲线是一段时间内收益率变动的可视化展示，具有一定的趋势性，是投资决策的重要依据。只要获取未来某一时段某一期限的收益曲线，则各交易期限所对应的收益率就可以获取，并且整体的国债收益率走势一目了然。投资者可以运用国债收益率曲线，判断未来一段时间内国债收益率走势，预先制定相应的债券交易策略，配置持仓国债结构，减少因国债交易的不确定性而造成的损失，避免交易风险，增加债券操作空间，进一步提高债券收益。

后疫情时代，2021年以来，国内经济持续向好，稳步复苏，但海外疫情依然严峻，国内局部疫情偶发，对经济恢复造成干扰，叠加美元流动性泛滥推升大宗商品价格大幅走高，市场通胀预期升温，对货币政策的进一步宽松形成掣肘。央行强调保持货币政策的连续性、稳定性和可持续性，保持对经济必要的支持力度，在合理充裕的流动性货币政策环境下，如何全面准确预测收益率曲线一直是投资者研究的热门话题。本文基于ARMA模型对国债收益率进行预测，帮助投资者依据预测结果制定、调整相应的国债交易策略，不断提高规避债券风险能力和提高债券收益率。

1 数据及模型介绍

1.1 ARMA模型

ARMA （p，q）模型，即自回归移动平均模型，是研究时间序列模型的重要方法，利用历史数据预测未来一段时间的走势，将自回归模型（简称AR模型）与移动平均模型（简称MA模型）为基础，“混合”结合在一起的时间序列模型。

一般ARMA（p，q）模型可以表示为：

其中，ℰt是白噪声序列，p和q是非负整数，AR和MA模型是ARMA模型的特殊情况，当p=0时，ARMA模型为MA（q），当q=0时，ARMA模型为AR（p）。

1.2 数据来源

目前，国内债券市场主要由银行间市场、交易所市场和商业银行柜台市场构成。其中，银行间债券市场具有债券交易量大、参与交易机构多、国债品种丰富、交易活跃程度高、债券期限分布密集等优点。10年期国债收益率是国家信用担保的长期债券，通常被作为无风险收益率，是股票市场，包括期货市场、房地产市场的资产价格均取决于10年期国债收益率。在国内债券市场中，10年期国债收益率是人民币资产定价的基础，债券活跃度较高。因此，本文使用银行间债券市场中1年期国债到期收益和10年期国债到期收益数据为研究对象，选取2021年1月1日—2021年8月31日共计166数据作为训练集， 对国债收益率曲线进行估计，用来进行国债收益率曲线的预测。

2 实证分析及预测

2.1 原始数据处理

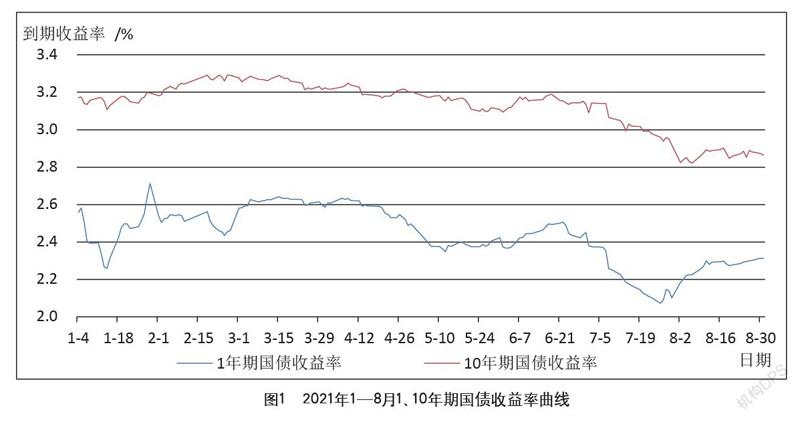
2021年1月1日—2021年8月31日，1年期和10年期国债收益率数据走势如图1所示。

从图1可以看出，1年期国债收益率曲线在2021年1—2月，国债收益率曲线波动较大，3—6月波动较缓，7月收益率曲线快速下滑至2021年最低点2.07%。10年期国债收益率曲线在2月震荡上行至3.22%后，至8月末，除6月中旬小幅震荡外，总体处于下行阶段，8月2日收益率至全年收益率最低点2.82%。

整体来看，1年期和10年期国债交易日数据曲线波动存在一定的关联性，整体曲线走势大致相同，1年期国债收益率曲线震动波幅明显，反应更加灵敏，10年期国债收益率曲線走势相对平缓。2021年，国债收益率曲线在2月底3月初小幅震荡上行，但总体收益率曲线呈下行趋势。

本文运用SPSS软件，建立ARMA 模型进行分析。从图2可以看出，1、10年期国债收益率序列的自相关图（ACF）和偏自相关图（PACF）自相关衰减缓慢，都是拖尾的，说明序列是非平稳的。ARMA模型需要平稳序列数据，对1、10年期国债数据进行一阶差分，观察序列是否平稳。

2.2 模型构建

2.2.1 1年期国债收益模型

从图3可以看出，1年期国债收益率自相关和偏自相关一阶不在置信区间内，从二阶开始全部落入置信区间内，故1年期国债收益率ARMA 模型可以考虑p，q取值，p∈[1，2]，q∈[1]。

1年期国债ARMA（1，1，1）和ARMA（2，1，1）模型R2均为0.994，调整R2均为0.83;ARMA（1，1，1）系数显著性和t值均优于ARMA（2，1，1）。

从图4可以看出，ARMA（1，1，1）残差序列样本自相关系数都落入随机区间内，因此，该模型能够有效拟合序列的走势。

模型表达式为：

2.2.2 10年期国债收益模型

从图5可以看出，10年期国债收益率自相关系数和偏自相关系数一阶全部落入置信区间内，因此选取了ARMA（1，1，1）。

10年期国债ARMA（1，1，1）模型R2均为0.983，调整R2均为0.983。从图6可以看出，ARMA（1，1，1）残差序列样本自相关系数都落入随机区间内，建立的模型随机误差项是一个白噪声序列，因此该模型能够有效拟合序列的走势。

圖4 1年期国债残差序列图

模型表达式为：

3 结语

本文基于国债收益率曲线的估计与预测，由于债券的收益率曲线受风险评估、债券供求关系、债券相对收益、通胀预期、短期长期利率与通胀预期、债市现金流与利率时机、货币政策、财政政策等因素影响，依据不同的到期国债收益率曲线预测未来一段时间内收益率曲线为投资者提供一定的数据参考，以达到获取超额利润的目标。

图6 10年期一阶差分国债收益率残差图

一是本文构建ARMA模型，通过对2021年1—8月国债收益率曲线参数估计，预测9月部分国债收益率曲线走势和收益率，1、10年期国债收益率曲线在一阶差分全部落入区间内，且拟合程度较好。

二是后疫情时代，从国债收益率曲线波动来看，短期国债收益率曲线波动幅度高于长期，在ARMA模型中，参数估计曲线预测效果与实际相差较大，且不理想。

三是在后疫情时代，收益率曲线是投资决策的重要依据，传统国债分析方法主要依靠麦考利久期和凸度进行债券投资组合分析，但必须要求收益率曲线平行移动，对非平行移动的债券分析不适用。

四是在制定国债交易策略方面，本文利用ARMA模型预测国债收益率曲线，根据“低买高卖”选取交易策略，不断改进交易标的，实现超额收益。

参考文献

王志强，康书隆.Nelson-Siegel久期配比免疫模型的改进与完善[J].数量经济技术经济研究，2010（12）：133-147.

陈蔚，马骏驰，赵耀文.我国国债收益率曲线的实证研究[J].经济与管理评论，2011（3）：118-123.

周子康，王宁，杨衡.中国国债利率期限结构模型研究与实证分析[J].金融研究，2008（3）：131-150.

胡泽俊，马伟力.我国国债收益率曲线构造实证研究[J].统计与决策，2013（10）：170-172.

Reflection on Bond Investment in the Post-pandemic Era

—— Based on Analysis of ARMA

Rural Credit Cooperatives in Gansu  SU Rong

Abstract： In recent years， in the inter-bank bond market， incidents of the Baoshang Bank Limited， private enterprises such as Tianqi Lithium， Tsinghua Unigroup and other state-owned enterprises such as Yongmei， have continuously appeared one by one because of their noncompliance， with frequent occurrence of bond default incidents and increase of negative public opinion from financial institutions. Government bonds are more and more chosen by investors for their profitability， safety and liquidity. This article is based on the ARMA model to predict the yield of government bonds， to help investors formulate and adjust corresponding trading strategies of government bonds based on the forecasting results， and continuously improve the ability to avoid bond risks and increase bond yields.

Keywords： ARMA model; government bonds; yield curve