超高性能混凝土柱的抗震性能分析

方 志， 方文昌， 胡 锐， 董长征

(1.湖南大学 土木工程学院， 湖南 长沙 410082； 2.湖北省交通投资集团有限公司， 湖北 武汉 430050)

超高性能混凝土(Ultra-High Performance Concrete，UHPC)是20世纪90年代国外研发的一种具有超高强度和优异耐久性的新型水泥基复合材料[1]。UHPC的抗压比强度(抗压强度/材料容重)约为普通混凝土的4倍，由此可显著减小配筋混凝土构件的截面尺寸，从而减轻结构自重、增加结构的变形能力、减小结构的地震作用[2]；此外，UHPC的高韧性和高延性可使结构吸收更多的地震能量，从而增强结构的抗震能力[3]。因此，与普通混凝土结构相比，采用UHPC有望形成抗震性能更为优越的配筋混凝土结构。

ZOHREVAND P[4]等对柱脚两倍塑性铰长度范围内采用UHPC代替普通混凝土的混合桥墩进行了拟静力试验试验，结果表明：UHPC可以显著提高试件的耗能能力。PALACIOS[5]等对塑性铰区采用UHPC的柱进行了拟静力试验，结果表明：UHPC柱具有良好的抗震性能，柱的配箍率可相应降低。MARCHAND P[6]等对无箍筋或配少量箍筋UHPC柱的抗震性能进行了试验研究，结果表明：箍筋的作用较小，尤其是轴压比较大时更是如此。

赵冠远[7]等对4根UHPC柱进行了拟静力试验，结果表明：UHPC柱抗震性能良好，箍筋对UHPC柱约束作用不明显。王诚[8]等对3根UHPC箱型墩进行了拟静力试验，结果表明：UHPC箱型墩抗震性能良好，水平荷载方向角是影响抗震性能的一个重要因素。鞠彦忠[9]等对18根UHPC柱进行了拟静力试验，结果表明：轴压比越大，试件承载力越高，延性越差；配筋率、配箍率越大，试件延性和耗能能力均越好；增加钢纤维掺量，可提高柱的延性和耗能能力。

现有研究均表明UHPC柱抗震性能良好，但相关研究仍较有限。基于此，本文采用开源有限元软件OpenSees(Open System for Earthquake Engineering Simulation)建立了UHPC柱全过程受力的分析模型，并对UHPC柱进行了拟静力试验，获得了柱的全过程受力形态，用以验证分析模型的适用性；基于被试验结果验证的有限元模型，对试件受力全过程进行了数值模拟，分析了不同参数对UHPC柱抗震性能的影响。

1 试验概况

1.1 试件设计

试件尺寸和配筋如图1所示。柱总高为3 600 mm，中部净高为2 800 mm，截面为200 mm×300 mm矩形截面，采用强度等级为150 MPa的UHPC浇筑，UHPC为商品预混料，钢纤维体积含量2%、长度13 mm、直径0.2 mm、抗拉强度≥2 000 MPa；用于柱顶端加载和底部固定的柱帽和底座高均为400 mm，采用C50混凝土浇注；柱纵向采用6根直径16 mm的HRB500钢筋，截面上对称布置，箍筋采用直径8 mm、间距200 mm的HRB400钢筋。试件制作时先浇筑UHPC柱体并采用蒸汽养护，浇筑完成静置48 h后，再使用90 ℃蒸汽养护48 h。UHPC柱养护完成后，再浇筑两端的普通混凝土柱帽和底座。普通混凝土浇注前，将UHPC柱内预留纵筋深入其内足够锚固长度并将预制UHPC柱体伸入底座和柱帽各3 cm，以保证预制件与后浇部分的整体性。实测试件所采用材料性能的特征值分别如表1和表2所示，表1中C50抗拉强度根据文献[10]计算，其余均为实测值。

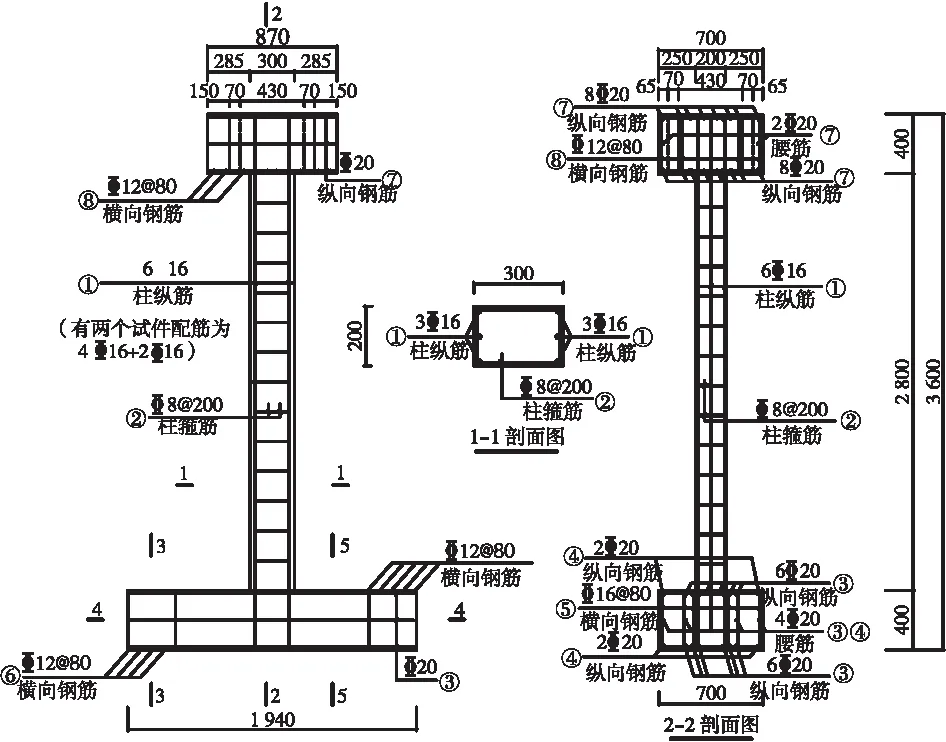
图1 试件尺寸及配筋(单位： mm)Figure 1 Diemnsion and reinforcement of specimens(Unit: mm)

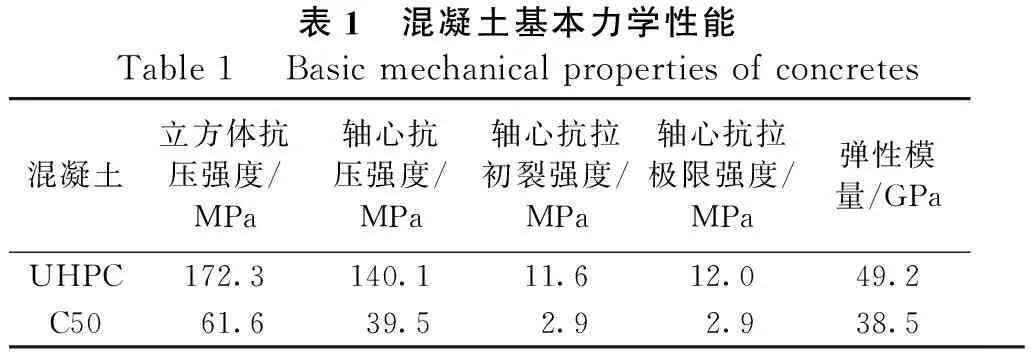
表1 混凝土基本力学性能Table 1 Basic mechanical properties of concretes混凝土立方体抗压强度/MPa轴心抗压强度/MPa轴心抗拉初裂强度/MPa轴心抗拉极限强度/MPa弹性模量/GPaUHPC172.3140.111.612.049.2C5061.639.52.92.938.5

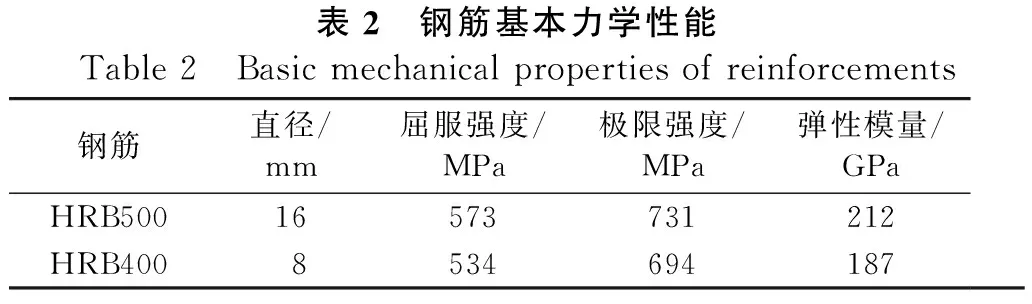
表2 钢筋基本力学性能Table 2 Basic mechanical properties of reinforcements钢筋直径/mm屈服强度/MPa极限强度/MPa弹性模量/GPaHRB50016573731212HRB4008534694187

1.2 加载装置和方案

试件采用多功能结构试验装置(Multi-Usage Structural Testing System，MUST)进行加载，加载装置如图2所示。轴压力通过4个竖向作动器施加，水平荷载通过2个水平作动器施加，先加竖直荷载至额定值，再施加水平荷载至柱破坏。柱试验轴压比为0.1，相应的轴压力840 kN。

图2 加载装置Figure 2 Loading set-up

参照相关试验规程[11]及文献[12]，对试件采用基于层间位移角控制的位移控制加载，加载制度见表3。每级荷载循环3次，直至试件破坏或荷载降低至极限承载能力的85%以下。

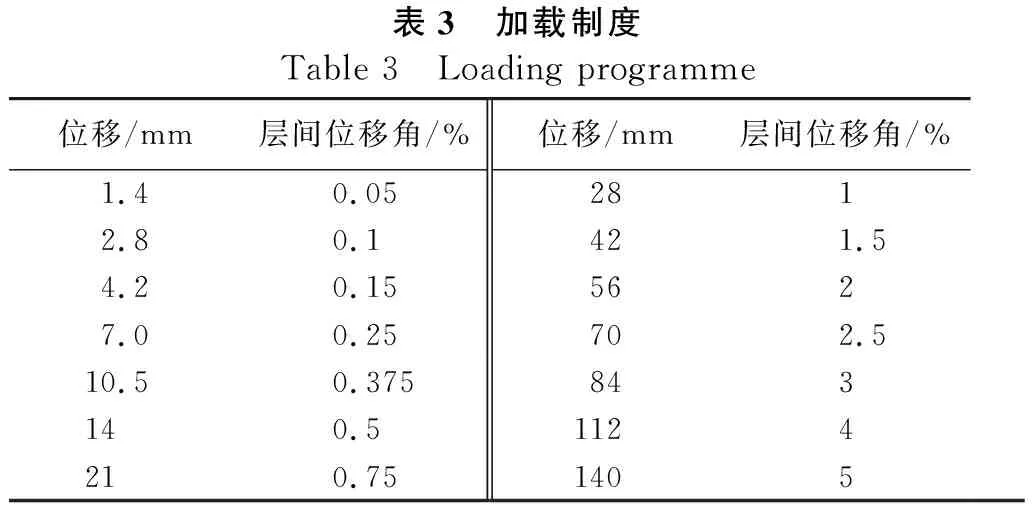
表3 加载制度Table 3 Loading programme位移/mm层间位移角/%位移/mm层间位移角/%1.40.052812.80.1421.54.20.155627.00.25702.510.50.375843140.51124210.751405

1.3 试验现象

位移小于6.3 mm时，水平荷载为79.6 kN，试件未出现裂缝，荷载-位移曲线呈线性，无残余变形；位移达到7.8 mm时，水平荷载为94.5 kN，试验柱左上角出现初始裂缝，宽度为0.01 mm；位移达到20.0 mm时，水平荷载达到峰值127.3 kN，试验柱四个角均有裂缝产生，最大裂缝宽度为0.07 mm；此后，试件水平荷载开始下降；位移达到55.7 mm时，水平荷载下降至124.1 kN，柱顶裂缝继续发展，正向裂缝与负向裂缝交叉，最大裂缝宽度为0.18 mm，并且在试验柱的拐角处观察到局部混凝土压碎；位移达到105.5 mm时，最大裂缝宽度为0.23 mm，水平荷载下降至103.2 kN，为极限承载能力的83%，判定试件破坏，终止加载并卸载。试件破坏形态与裂缝分布如图3所示。

图3 试件破坏形态与裂缝分布Figrue 3 Failure modes and crack distribution of specimens

2 分析模型建立

2.1 截面与单元类型选取

OpenSees中截面恢复力模型有弹性模型、理想弹塑性模型、双折线强化模型等常规模型和比较精细的纤维模型。纤维模型是将截面划分为一定数量的离散小纤维，并可在各纤维内定义不同的材料本构关系，可较好地反映出截面的材料特性和钢筋分布特点，因此本文选用纤维截面模型。

OpenSees中非线性梁柱单元(Nonlinear Beam-Column Elements)分为基于力的梁柱单元和基于位移的梁柱单元，前者计算精度高但不易收敛，后者易于收敛但精度比前者稍低，不过可以通过增加单元数量来提高计算精度，因此本文选用基于位移的梁柱单元。

2.2 材料本构关系

UHPC采用OpenSees中基于Thorenfeldt曲线的Concrete06 Material本构，相关参数取UHPC材料的测试值；卸载方式为分段线性卸载，卸载与再加载路径取为不同，以便更准确地模拟混凝土的滞回特性，Concrete06的应力 — 应变关系滞回本构如图4所示[13]。

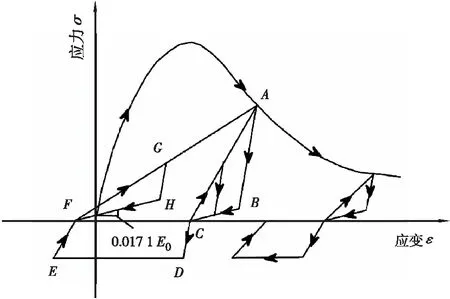
图4 UHPC的滞回本构Figure 4 Constitutive relationship of UHPC

UHPC单轴受压本构方程为式(1)：

(1)

式中：σc为压应力；fc为轴心抗压强度；εc0为峰值压应变；n为受压应变-应变曲线形状系数，取n=2；k为峰值压应变后应力 — 应变曲线形状系数，取k=1.33。

UHPC单轴受拉本构方程为式(2)：

(2)

式中：σt为拉应力，E0为弹性模量；fte为轴心抗拉初裂强度；εte为初裂应变，且εte=fte/E0；εtu为极限拉应变；b为受拉应变-应变曲线形状系数，取b=0.05。依据文献[14]的研究结果，取：

fte=ft0(1+αtλf)

(3)

(4)

式中：ft0为基体抗拉强度，根据文献[15]ft0=0.047fcu，k；钢纤维影响系数t=0.32；钢纤维特征参数λf=ρflf/df，ρf、lf、df分别为钢纤维的体积掺量、长度和直径。

根据材性试验和文献[15]，定义UHPC本构时的参数取值如下：fc为140.1 MPa，εc0为3.20×10-3，E0为49.2 GPa，fte为11.6 MPa，εtu为3.88×10-3。

钢筋采用基于Giuffre-Menegotto-Pinto模型的Steel02 Material本构，其采用应变的显函数形式，计算效率高，同时也考虑了等向应变硬化和包辛格效应的影响，钢筋的应力-应变关系本构模型如图5和式(5)所示。

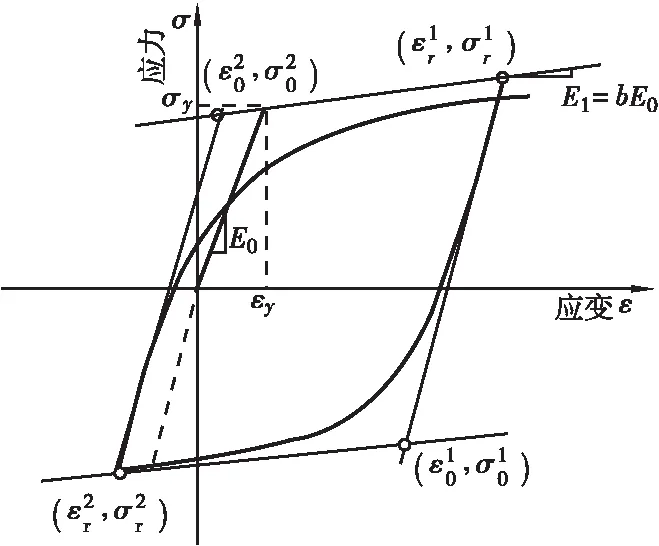
图5 钢筋本构Figure 5 Constitutive model of reinforcement

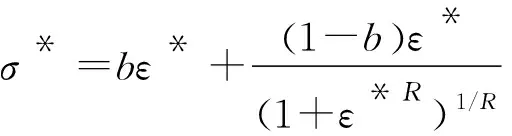
(5)

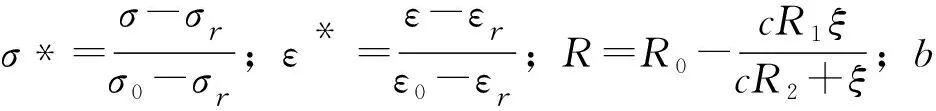
根据材性试验和OpenSees用户手册，定义钢筋本构时的参数取值如下：钢筋为HRB500，fy为573 MPa，E为212 GPa，b为0.01，R0为18.5，cR1为0.925，cR2为0.15。

2.3 结果对比

图6为试件受力变形性能模拟值与试验值的比较，峰值点处极限承载能力及相应水平位移实测值分别为127.3 kN和20.04 mm，相应的预测值分别为127.7 kN和19.60 mm，受力全过程的预测结果与试验结果吻合较好，验证了所建立分析模型的适用性。

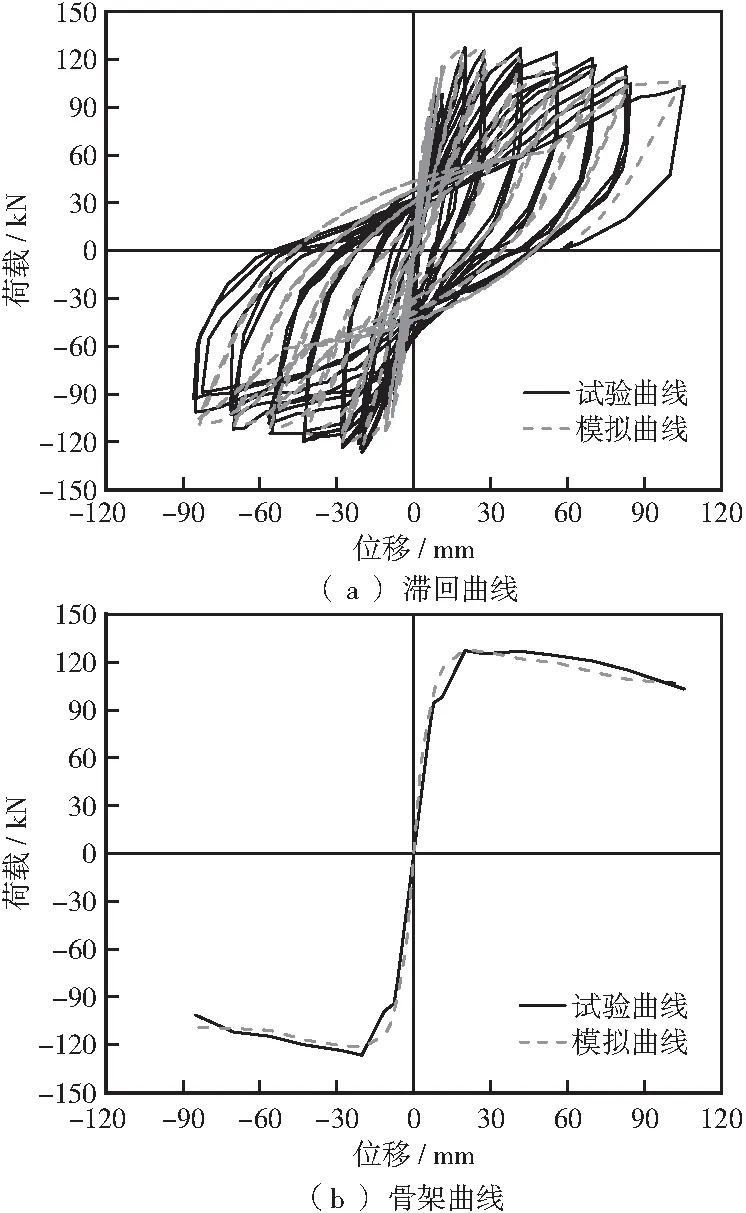
图6 模拟结果与试验结果对比Figure 6 Comparison of the predicted and the measured results

3 参数分析

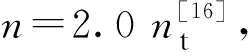
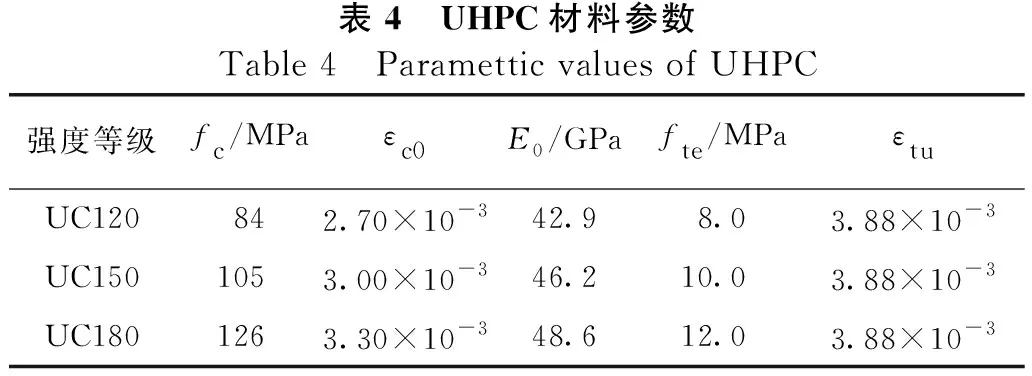
表4 UHPC材料参数Table 4 Paramettic values of UHPC强度等级fc/MPaεc0E0/GPafte/MPaεtuUC120842.70×10-342.98.03.88×10-3UC1501053.00×10-346.210.03.88×10-3UC1801263.30×10-348.612.03.88×10-3

各试件计算结果见表5，试件编号中N、R和S分别表示轴压比、纵筋配筋率和UHPC强度3个参数，其后的数字表示对应参数的取值；屈服位移按照等能量法[17]计算，极限位移为荷载下降至极限承载能力85%时对应的位移。

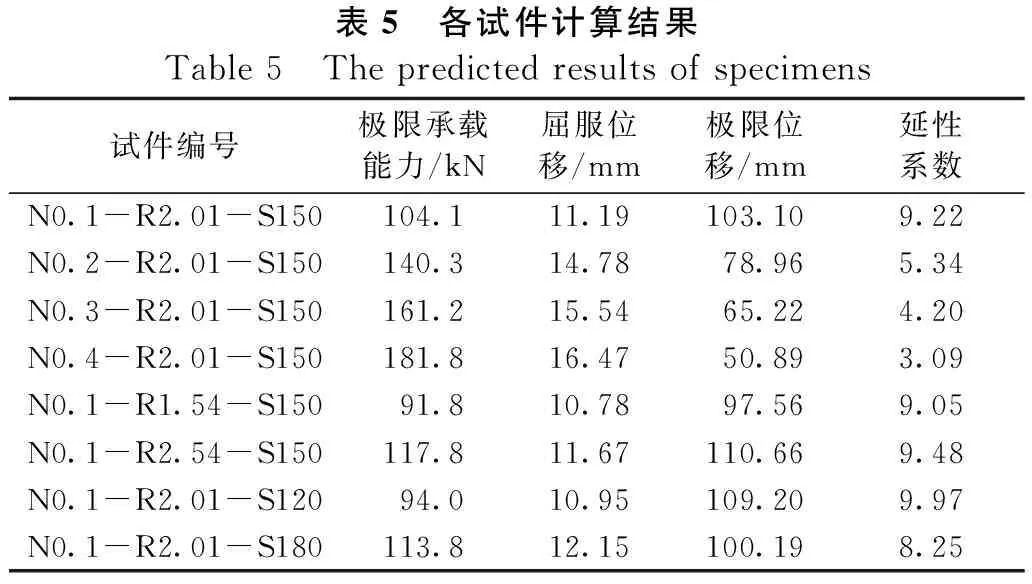
表5 各试件计算结果Table 5 The predicted results of specimens试件编号极限承载能力/kN屈服位移/mm极限位移/mm延性系数N0.1-R2.01-S150104.111.19103.109.22N0.2-R2.01-S150140.314.7878.965.34N0.3-R2.01-S150161.215.5465.224.20N0.4-R2.01-S150181.816.4750.893.09N0.1-R1.54-S15091.810.7897.569.05N0.1-R2.54-S150117.811.67110.669.48N0.1-R2.01-S12094.010.95109.209.97N0.1-R2.01-S180113.812.15100.198.25

所有试件的延性系数均大于3，表现出良好的抗震性能；若以位移延性系数不小于3为目标，则UHPC柱的设计轴压比限值为0.8。

3.1 轴压比

轴压比对试件抗震性能的影响如图7所示，由于试件模拟骨架曲线正负向基本对称，故仅取正向骨架曲线进行分析。可知：在加载初期，试件处于弹性状态，不同轴压比下试件的初始刚度相同，线性段重合，而轴压比越大，试件的线性段越长，开裂荷载与位移均越大，骨架曲线下降段越陡峭；轴压比从0.1增大到0.4，试件的极限承载能力增大75%，屈服位移增大47%，极限位移减小51%，导致延性系数减小66%。

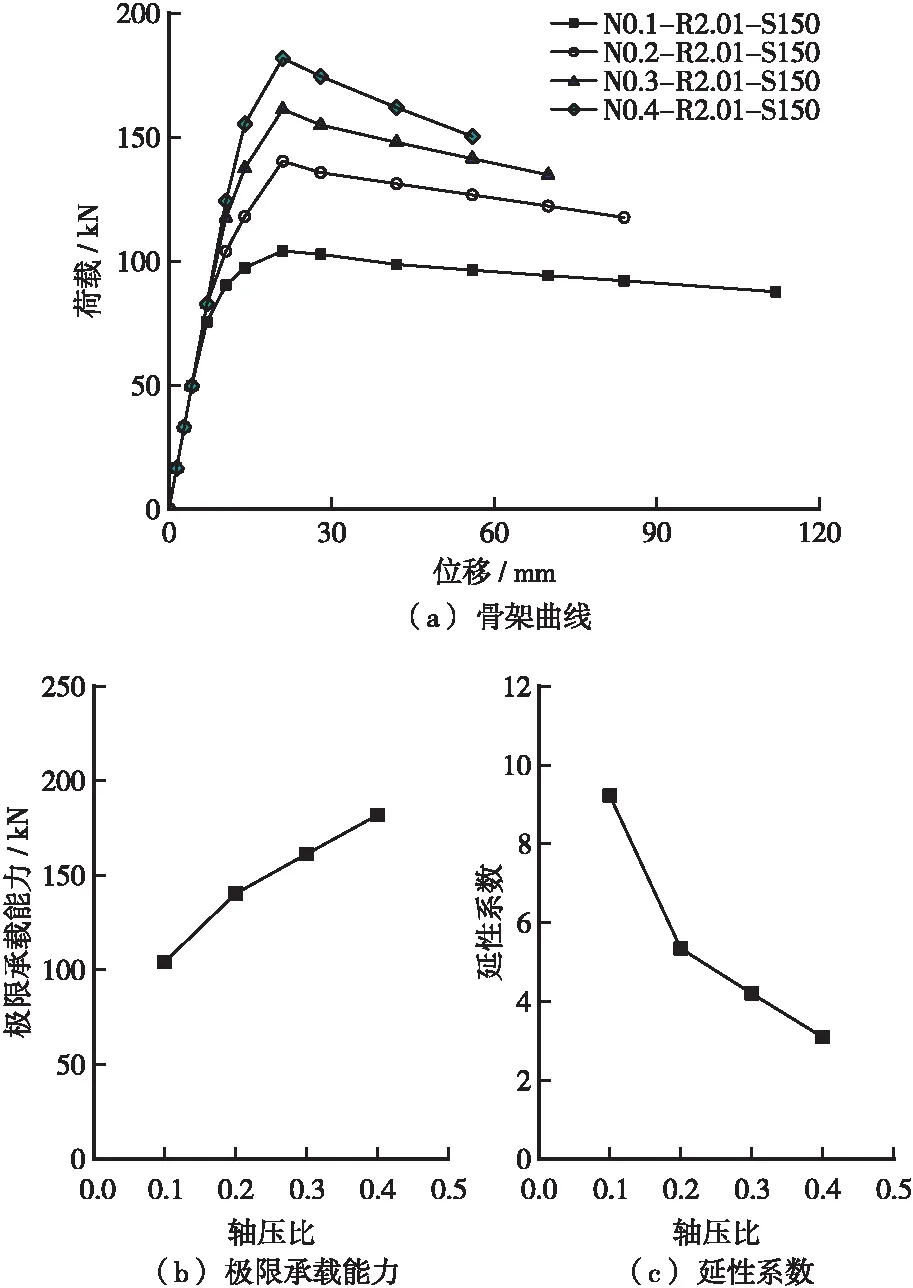
图7 轴压比对试件抗震性能的影响Figure 7 Effect of axial loading ratio on seismic performance of specimens

3.2 纵筋配筋率

纵筋配筋率对试件抗震性能的影响如图8所示。可知：不同纵筋配筋率试件的骨架曲线初始刚度基本相同，试件极限承载能力随纵筋配筋率的增大而增大；纵筋配筋率从1.54%变为2.54%，增大65%时，试件极限承载能力增大28%，屈服位移增大8%，极限位移增大13%，延性系数增大5%。

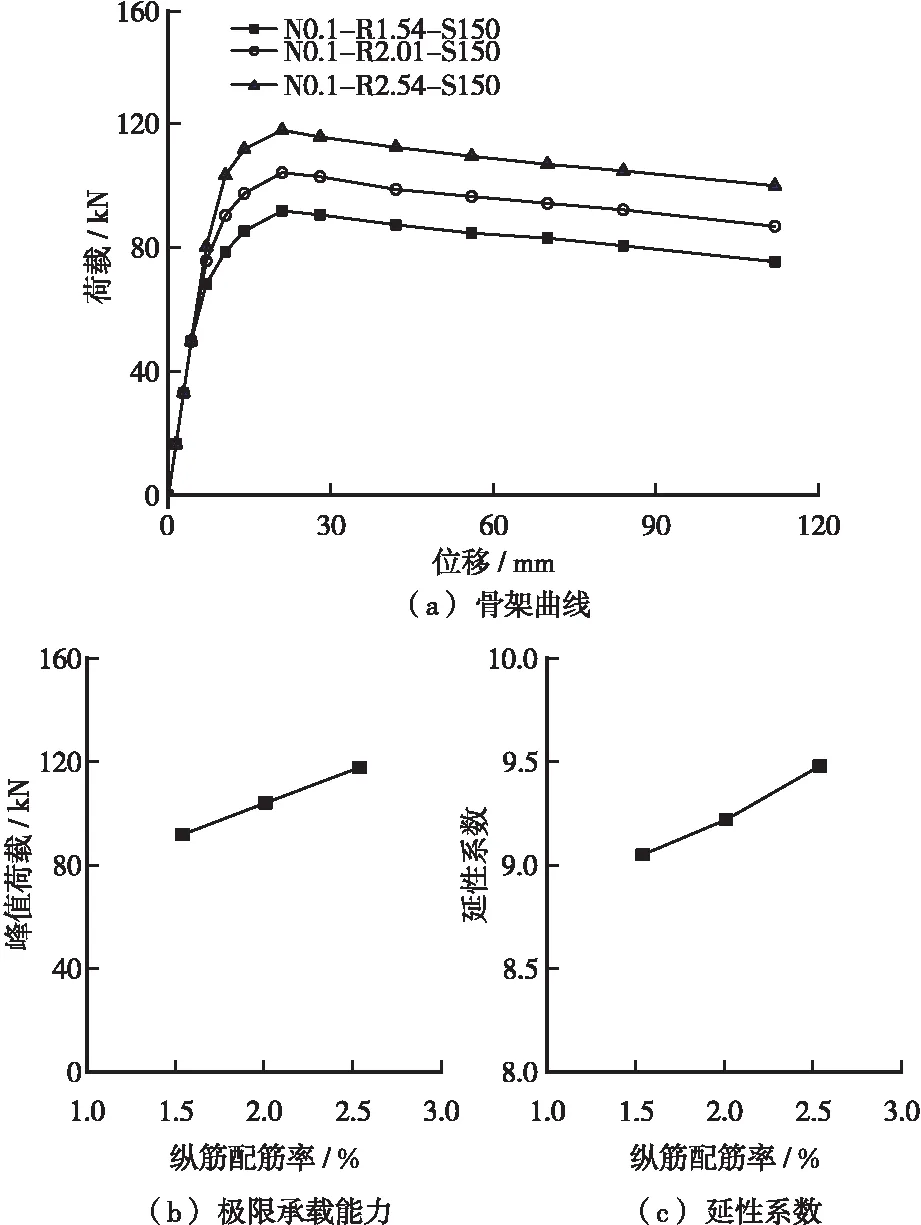
图8 纵筋配筋率对试件抗震性能的影响Figure 8 Effect of longitudinal reinforcement ratio on seismic performance of specimens

3.3 UHPC强度

UHPC强度对试件抗震性能的影响如图9所示，可知：随着UHPC强度等级的增大，试件初始刚度和极限承载能力均增大，UHPC强度等级从UC120提高到UC180，试件初始刚度增大10%，极限承载能力增大21%，屈服位移增大11%，极限位移减小8%，延性系数减小17%；由表5可知，随着UHPC强度等级的增大，其峰值压应变增大，极限压应变减小，由此导致试件的延性降低。

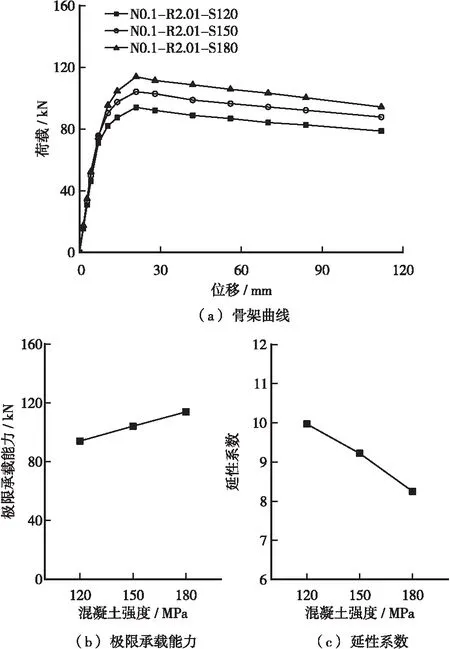
图9 UHPC强度对试件抗震性能的影响Figure 9 Effect of UHPC strength on seismic performance of specimens

4 结论

采用有限元软件OpenSees对UHPC柱的抗震性能进行了分析，并以试验验证了分析模型的适用性，基于分析结果，得到以下结论：

a.模拟得到的滞回曲线和骨架曲线与试验结果吻合较好，说明模型对材料本构、截面、单元类型选取合理，数值模型可以较好地模拟UHPC柱的受力性能。

b.轴压比对试件抗震性能影响显著，轴压比从0.1提高到0.4，试件极限承载能力增大75%，极限位移减小51%，延性系数减小66%；纵筋配筋率从1.54%增大到2.54%，试件极限承载能力增大28%，延性系数增大5%；UHPC强度等级从UC120增大到UC180，试件初始刚度增大10%，极限承载能力增大21%，延性系数减小17%。

c.所有试件延性系数均大于3，抗震性能良好；若以位移延性系数不小于3为目标，则UHPC柱的设计轴压比限值可取为0.8。