基于加速度传感器的电机振动数据处理

夏欣 方挺 黄健

安徽工业大学 安徽 马鞍山 243032

1 无限振动传感器标定

根据误差产生机制不同，MEMS加速度计的误差主要包括零位偏差、标度系数误差、安装误差及轴间非正交误差等。对于MEMS加速度计，其造成精度偏差的主要原因是零位误差和标度系数误差。安装误差及轴间非正交误差在较长时间内不会产生大的变化，且安装及制造水平提高能有效减少此类误差，所以可以忽略不计。根据以上分析，建立加速度计ADXL357的输出误差数学模型为：

其中：Dx，Dy，Dz是加是速度计输出的真实加速度，Sx，Sy，Sz为加速度计的比例因子，Mx、My、Mz是加速度计的测量值，Bx、By、Bz是加速度计的零位偏差。

由公式1-1可知，需要通过标定计算出加速度计ADXL357的比例因子零位偏差。加速度计标定通常采用多位置翻滚标定法，常用的有6位置标定法[1-2]、10 位置标定法[1-2]、12位置标定法[1-2]。多位置翻滚标定需要三轴转台才能完成，而三轴转台价格昂贵，基于实验室条件限制，本文设计了一种基于气泡水平仪和长方体盒装物实现简易六位置标定方法。

图1给出了简易六位置标定法的示意图。

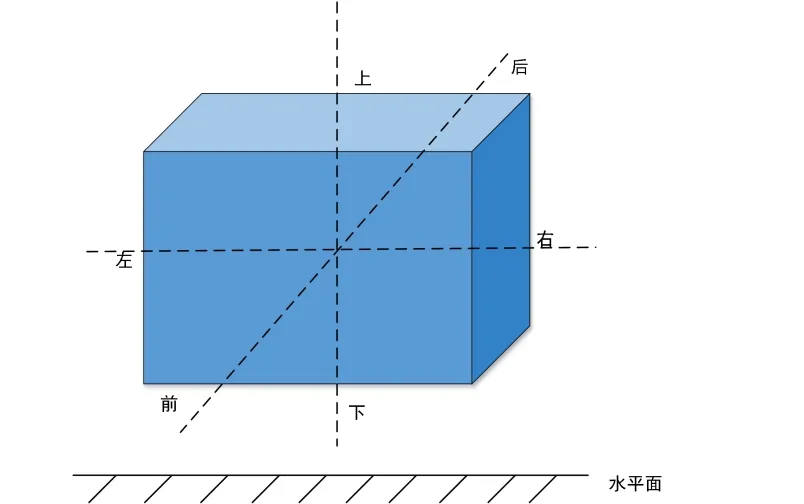
图1 简易六位置标定示意图

将无线振动传感器按照长方体六个面进行固定即可得到六个标定位置（位置1～6），并使用水平仪寻找水平面位置[3]。依次按照位置1～6放置无线振动传感器，并记录其对应位置的实际加速度值，表1给出了简易六位置标定的具体描述。

表1 简易六位置标定表

通过式2可计算X轴的零位偏差，同理可得Y、Z轴的零位偏差By和Bz。

其中：X+g和X-g分别为ADXL357处于位置1和位置2时的实际加速度输出值，通过式3可以计算出X轴的比例因子Sx，同理可计算出Y轴和Z轴的比例因子Sy和Sz。ADXL357的量程为±10g，ADXL357内部集成了20位的模数转换器，当加速度为1g时，其输出应该为52428个LSB。

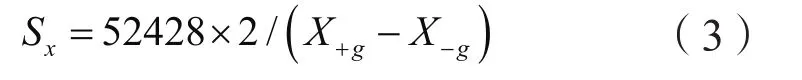
通过上述标定方法可以得到 ADXL357 的零位偏差和比例因子如表2所示。

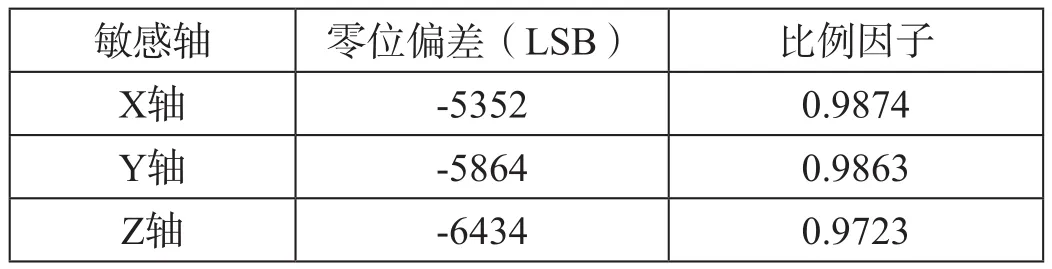
表2 ADXL357零位偏差和比例因子

将表2中的零位偏差和比例因子作为系统参数写入单片机的Flash存储器进行保存，无线振动传感器在每次开机之后将参数从Flash中加载至SRAM中，在检测振动加速度的过程中使用这些参数计算得到标定后的加速度 值，以提高加速度检测的精度。

2 振动数据处理

振动传感器通过三轴MEMS加速度计ADXL357采集X，Y，Z三个轴向的原始振动加速度，原始振动加速度包含了重力加速度分量，需要对原始振动加速度进行分解，去除重力加速度分量，获取线性加速度；对线性加速度序列进行FFT运算，获取高分辨率振动加速度频谱[4]；为了进一步降低无线通信的数据 传输开销，对高分辨率的振动加速度频谱进行频谱压缩；最终制作成无线数据包。 ADXL357的机械系统可以将视为弹簧-质量阻尼系统。

当外部加速度作用于ADXL357时，质量块受到惯性力，惯性力使弹簧产生形变，从而产生了位移，通过ADXL357内部的特殊构造将位移变化映射为电容变化，然后通过内部电容到电压的转换电路将电容变化转换为电压变化，从而得到加速度与电压之间的线性关系。

基于上述变换过程，根据牛顿第二定律有：

其中：Am为质量块的加速度，Fs为质量块受到的合外力，m为质量块的质量，重力始终会影响测量的加速度值，公式5可以表示为：

其中：F为除重力之外质量块所受合力，其中，。

前文提到，ADXL357在静止状态下，其垂直于水平位置的轴向加速度接近与1g，但在实际测量中，由于电机的形状以及为操作方便考虑，加速度传感器的安装无法做到十分精确，ADXL357的X、Y、Z三轴所处的实际坐标系，会与标准坐标系之间存在一定夹角，重力加速度分量作用于X、Y、Z三轴的具体数值，与该夹角有关，当振动传感器以不同位置及角度安装在电机上时，重力加速度的分解状态也不一致，这会导致对电机振动加速度的测量产生不同的影响[5]。

若不进行处理，ADXL357获取的振动加速度数值中，包含了因重力块的重力作用所产生的重力加速度分量，因而为了测量出电机的真实加速度值，需要去除重力加速度分量得到线性加速度，为了消除重力加速度分量，使用低通滤波器将重力加速度进行分离，然后将测量值减去重力加速度分量，所得即为线性加速度。由一阶低通滤波器算法：

可得X、Y、Z轴重力加速度分量：

计算线性加速度：

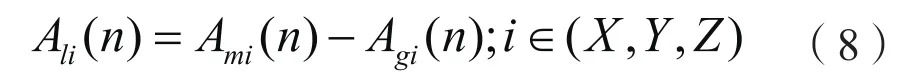
采样周期可由式10计算得到：

图2为执行加速度分解算法后的加速度序列，采样频率为1KHZ，采样点数为1000，滤波系数α为0.94。

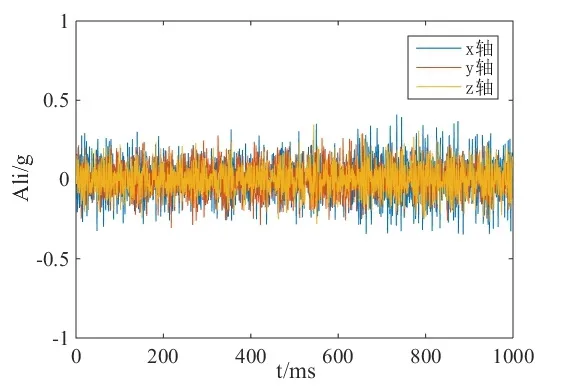
图2 加速度分解图

由图2可知，经过加速度分解之后有效去除了原始加速度序列中的重力加速度分量，得到电机振动加速度值。