一课一题复习课的研究

李孟虹

一、教学目标

（一）对二元一次方程、二元一次方程组的概念、解及解法进行了解。

（二） 通过导入问题情境、建立模型、求解、解释与应用四个步骤，感受数学建模思想。

（三） 构建本章的知识结构。通过思考、探索等活动，体会消元思想、整体思想、换元思想，提高学生自主学习能动性与对问题的深入探究性。

二、教学内容设计

（一）情景引入

老师：同学们，现在我手中有一根绳子，长度是5m。如果我用剪刀将这根绳子分成两段，那么这两段的长度分别是多少呢？

探究1：绳子长为5m，剪成两段，长度分别是多少？

数学模型：假设其中一根绳子的长度是 xcm ，另一根是 ycm，

x+y=5

这个方程的解有无数组，所以对应情况也有无数种。

【设计意图】让学生对数学建模过程进行深入了解，通过情景导入，激发学生学习兴趣的同时，帮助学生将现实生活中的实际问题转化为数学中的方程模型。

复习回顾：知识点1：什么叫作二元一次方程

未知数项的次数是 1 并且含有 两个  未知数，这样的整式方程叫作二元一次方程。

【设计意图】“以题带点”复习，避免单调重复。

老师：同学们试着想一下，两段绳子的长度还有其他可能吗？

探究2：将一根 5m 的绳子剪成两段，若使两段绳长为整数，那么两段的长度分别是多少呢？

数学模型：假设其中一根绳子的长度是 xcm ，另一根是 ycm，x+y=5的整数解有哪几个？

（这个实际问题中x=1与y=1重复，x=2与y=2重复）

答：两段的长度分别是1m、4m或2m、3m.

复习回顾：知识点2：二元一次方程的解

讓二元一次方程两边的值相等的两个未知数的值，就称之为二元一次方程的解。

【设计意图】增加整数解的条件，从而过渡到复习二元一次方程的解的情况。

老师：同学们继续思考一下，怎样才能使两段绳子的长度只有唯一一种可能呢？

探究3：将一根 5m 的绳子剪成两段，且其中一段绳长的5倍比另一段绳长的3倍多1m，两段的长度分别是多少呢？

数学模型：设两段绳子的长度分别是 xm和ym.

复习回顾：知识点3：二元一次方程组的概念

一般地，含有两个相同的未知数的 两个二元一次方程合在一起，就叫作二元一次方程组。

【设计意图】要想得到唯一的解，那么就要在题目中增加一个条件，然后得到一个二元一次方程，接着将其与前面的方程就能组成一个二元一次方程组。

探究4：解方程（熟练运用代入消元法和加减消元法）解得

老师：解出来的结果不要忘记代入原方程组中检验，如果检验原方程组还能成立，那么结果就是原方程组的解，那么对于二元一次方程组的解是什么大家知道吗？

复习回顾：知识点4：二元一次方程组的解

通常，对于二元一次方程组，两个方程的公共解称之为二元一次方程组的解。

复习回顾：知识点5：二元一次方程组的解法

（1）二元一次方程组一元一次方程.

（2）现在我们用到的思想叫作消元思想，简单点来就是把未知数的个数变得越来越少、逐一解决，这种思想在解二元一次方程组的时候被经常用到.

（3）常用的方法包括代入消元法和加减消元法.

探究4：最后回到实际问题。

解：设两段绳子的长度分别是 xm和ym.

解这个方程组，得

答：两段的长度分别是 2m、3m.

【设计意图】以此题组为例，不仅帮助学生复习了之前所学的知识，还有利于学生熟练应用旧知识解决新题目，将如何解二元一次方程组的步骤和方法再一次进行复习。通过复习与学习新知识的完美结合，提高了学生运用旧知识解释并思考新知识的能力，更重要的是提升了学生的学习效率。

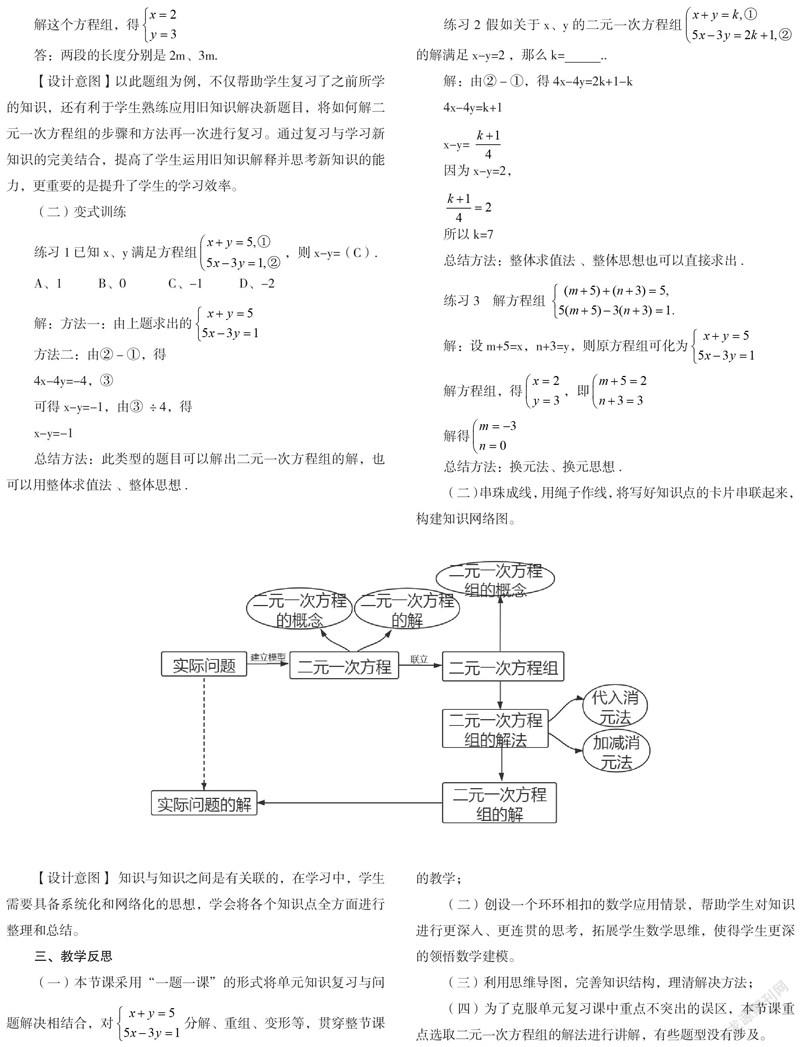
（二）串珠成线，用绳子作线，将写好知识点的卡片串联起来，构建知识网络图。

【设计意图】 知识与知识之间是有关联的，在学习中，学生需要具备系统化和网络化的思想，学会将各个知识点全方面进行整理和总结。

三、教学反思

（一）本节课采用“一题一课”的形式将单元知识复习与问题解决相结合，对分解、重组、变形等，贯穿整节课的教学;

（二）创设一个环环相扣的数学应用情景，帮助学生对知识进行更深入、更连贯的思考，拓展学生数学思维，使得学生更深的领悟数学建模。

（三）利用思维导图，完善知识结构，理清解决方法;

（四）为了克服单元复习课中重点不突出的误区，本节课重点选取二元一次方程组的解法进行讲解，有些题型没有涉及。