深度学习下“趣”味数学探究
摘 要 深度学习是基于学生理解、有效整合知识、激活高阶思维、创新解决问题的活动。游戏作为学生喜闻乐见的方式,能够引起小学生的学习兴趣,与深度学习有着必然的联系。深度学习离不开游戏设计,游戏的应用不是“为了游戏而游戏”,唯有促进深度学习方能让游戏展现其活力与应有的价值。深度学习下如何应用小学数学游戏,可以采用以下策略:精设情境,诱发兴趣;改变规则,激活乐趣;亲历体验,感悟智趣;对话思辨,融合理趣;变通求异,升华创趣,从而走向“深度学习,趣味共生”的大境界!
关键词 深度学习 数学游戏 游戏应用
深度学习是当代小学数学教学的核心问题。关于深度学习,安富海教授有过这样的论述:深度学习是一种基于理解的学习,是指学习者以高阶思维的发展和实际问题的解决为目标,以整合的知识为内容,积极主动地、批判性地学习新的知识和思想,并将它们融入原有的认知结构中,且能将已有的知识迁移到新的情境的一种学习[1]。游戏作为学生喜闻乐见的方式,与深度学习有着必然的联系。游戏要关于数学本质作好充分的准备,其不是为了演示明显的数学特征,而是应该作为活动激发学生的数学理解和高阶认知[2]。深度学习离不开游戏设计,有效的游戏能够激发兴趣,调动探索欲望,引发学生全身心投入,促使学生走向深度理解,思维纵深发展,解决问题更加灵活、高效;游戏的应用不是“为了游戏而游戏”,唯有促进深度学习方能让游戏展现其活力与应有的价值。深度学习背景下,如何应用小学数学游戏,可以采用以下策略:精设情境,诱发兴趣;改变规则,激活乐趣;亲历体验,感悟智趣;对话思辨,融合理趣;变通求异,升华创趣。
一、精设情境,诱发兴趣
游戏,离不开情境,可以是生活情境、问题情境、操作情境等等。这样的情境,充满着游戏意味,诱发着学习兴趣。精心设计游戏,要遵循学生的认知特点,贴近教学内容,让形式服务于内容并实现二者的有机统一。游戏的设计首先做到“趣”字当头,有时甚至让学生意想不到,真正做到有趣而学、因趣而生!
一位教师在教学古代名题“鸡兔同笼”问题:今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何时,设计了这样的“拼摆长方形”游戏情境:
用一种长方形的长表示鸡的只数,另一种长方形的长表示兔的只数,两种长方形的宽相同,均表示脚的只数2。请你动手摆一摆,看看能拼出哪些图形。
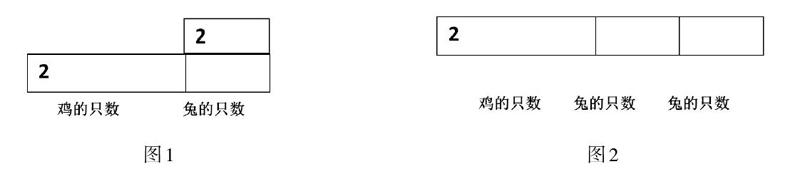
学生动手操作,拼摆出这样的一些图形(如图1、图2):
……
学生在拼摆图形后,教师抛出一串问题:每个大、小长方形的面积分别表示什么?拼成的图1、图2的面积分别表示什么?图1、图2中大长方形的长分别表示什么?
学生边拼图、边思考,在摆拼图形的过程中感受游戏的情趣,又带着思考去拼图,这样的游戏促发学生借助“几何直观”进行深度理解:图2中的大长方形长47(94÷2=47)相当于“鸡的只数+兔的只数×2”,图1中的大长方形的长35相当于“鸡的只数+兔的只数”,兔子的只数立刻求出:47-35=12(只),多么有趣的拼摆,多么巧妙的方法!学生为操作游戏的奇妙而感叹!
二、改变规则,激活乐趣
游戏的精彩程度,有时在于规则的变化。因规则,更多人投入,更多人思考,更多人挑战,游戏的竞争性就更强,游戏的乐趣因此喷薄而出!
以抢数游戏为例:
第一轮比赛:抢30。
比赛规则:(1)两个人从1开始依次轮流报数,每人每次只能报1个数或2个数,不能多报,也不能不报;(2)谁先报到30谁就获胜;(3)猜拳决定谁先报数(谁赢谁先报数)
第二轮比赛:抢40。
比赛规则:(1)两个人从1开始依次轮流报数,每人每次只能报1个数或2个数,不能多报,也不能不报;(2)谁先报到40谁就获胜;(3)猜拳决定谁先报数(谁赢谁先报数)
第三轮比赛:抢( )。
比赛规则:同桌合作,设计抢( )。写下获胜的秘诀。
抢30与抢40,规则看似相似,其实内藏玄机,有策略变化,激活思维。抢30,需要后发制人;抢40,需要先发制人,而为了获胜,每人总要想方设法抢到与30或40相差3的数据,以此类推:抢30就要依次抢到:30、27、24……3,要抢到3,只能“后出手”;抢40就要依次抢到:40、37、34……1,要抢到1,必须“先出手”。第三轮比赛,则是变中有变。学生进行规则设计比赛,这需要学生发现抢30、抢40的变化规律,具有开放性、拓展性、创造性。比赛中,学生有可能设计抢50、抢60等活动的规则,还有可能出现每人每次只能报1个数、2个数或3个数等等。规则之变,给学生的游戏探索带来广阔的探索天地。
游戏一般来说都有一定的规则,而不是随机的,都是按照一定的規则组织起来,并用规则来支配游戏。因为每一个活动都有独特的规则,改变规则,就支配了学生的活动,挑战的情趣会更加凸显。
三、亲历体验,感悟智趣
游戏活动往往是显性的、可观察的。在充满情趣的游戏中,让学生身临其境,去体验、感悟、发现数学中的规律,教学会更丰实、更生动,也更有数学价值。
在教学《确定位置》时,教师可以设计不同的现场游戏:
游戏一:互报数对找伙伴。游戏规则:两名同学结对,一名同学任意报数对,另一名同学找伙伴;看哪对同学既正确又迅速。
游戏二:师生互动找规律。游戏规则:教师报数对,学生听数对站立。
教师报出以下数对:
第一组是(3,1)(3,2)(3,3)(3,4)(3,5)(3,6);
第二组是(1,3)(2,3)(3,3)(4,3)(5,3)(6,3);
第三组是(1,1)(2,2)(3,3)(4,4)(5,5)(6,6);
……
游戏三:动脑想象定位置。游戏规则:根据条件信息,请对应位置的同学起立。
班长小明所在位置用数对(3,4)表示,其前、后、左、右相邻的每个位置分别用数对( )( )( )( )表示;从班长小明所在位置向后3个位置,再向左3个位置,表示为( )
……
“游戏一”中,游戏的目的在于让学生明确数对所表示的含义,进一步体会数对与位置一一对应关系。“游戏二”中,教师结合情境,抛出问题:站立的同学有什么现象发生?你有什么发现?同学们惊喜发现:数对中表示“第几列”的数相同,同一列同学站立,数对(3,□)不再对应某一个位置,而是与第三列所有位置对应;数对中表示“第几行”的数相同,同一行同学站立,数对(○,3)对应着第三列所有的位置;数对中表示“第几行”“第几列”的数相同,可以用数对(,)对应着所有第几列、第几行相同的位置。“游戏三”中,需要学生进行情景想象,利用规律,借助推理,确定每一个与之相邻的位置以及位置移动后对应的数对。
这一游戏,情境性很强。学生在亲身体验中感悟一一对应思想,发现数对中掩藏的一些规律。有了这样的亲历过程,学生对规律的认识更加丰实、深刻!
四、對话思辨,融合理趣
深度学习,离不开思辨。学生与学生、学生与教师之间进行对话、辩论、反思,使思维过程更加丰富、深刻,这样既展开游戏碰撞,又体现和谐共生,从而激扬着游戏精神,生成着游戏智慧!游戏体现了对话的特性[3]94。对话是游戏的内在本质,以游戏的对话精神关照教学,教学就是一种游戏性的对话活动。它是师生在愉悦、自由的情绪体验中,在相互尊重、信任、平等的基础上的精神相遇活动[3]179。
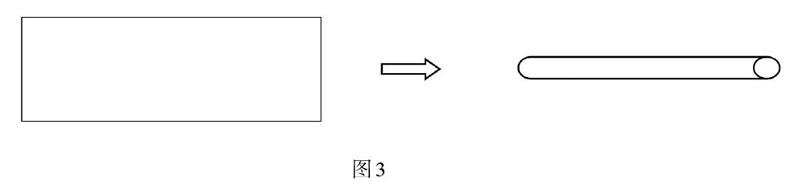
在教学《圆柱》的体积后,一名教师组织学生拿出一张长方形纸片,卷成一个圆柱(如下图3)
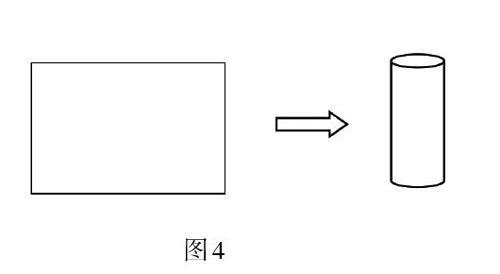
接着,教师让学生在进行撕一撕、卷一卷的动手操作游戏:将长方形纸张平均分成2份,卷成一个圆柱(如图4):
学生经历操作活动后,教师组织猜一猜:图4中卷成的圆柱体积与图3相比,有怎样的大小关系?
学生的对话活动十分精彩:
生A:我认为纸张变小,卷成的圆柱体积自然就小。
生B:因为纸张只有原来的一半,卷成的圆柱体积就是原来的一半。
生C:我认为,纸张变小,只是侧面积变小了,但体积有可能发生变化。
生D:卷成的两个圆柱相比,一个底面周长较短,但高较长;一个底面周长较大,但高较短,最好通过计算再比较。
……
在操作中,学生感受到纸张变“小”;在思辨中,学生进行“类比”推理,形成了这样的几种思维定势:圆柱纸张小,体积就小;圆柱侧面积是原来的一半,体积就是一半……
于是,教师对长方形进行了赋值,原来长方形纸片长62.8厘米,宽15.7厘米,让学生算一算、比一比:
图3圆柱体积:∏ × (15.7 ÷ 3.14 ÷ 2)2 × 62.8 = 392.5∏(立方厘米)
图4圆柱体积:∏ × (62.8 ÷ 2 ÷ 3.14 ÷ 2)2 × 15.7 = 392.5∏(立方厘米)
通过比较,学生发现,在这样的情况下,用纸片的一半也能卷出体积相等的圆柱。教师接着让学生自己为长方形纸片进行赋值,感受结果的多样性,消除在游戏中因直觉而产生的思维定势。
游戏虽然简单,但道理蕴涵其中。游戏给学生带来了乐趣,也容易让学生置身于认知“陷阱”,教师有效组织学生进行游戏思辨,适时引领、点拨,并带来了深度思考,必然会达成游戏教学理、趣相融的境界!
五、变通求异,升华创趣
现实生活多姿多彩,数学问题是丰富多样,借助多种策略解决问题能够拓宽学生的视野,提升学生的关键能力。而信息技术尤其是“动画”技术的运用,能够化静态为动态,在变通中活化思路,让课堂的游戏色彩更加浓郁。
有这样一道生活中的实际问题:
王大叔将一块正方形地分成四块种植蔬菜,先沿着第①块长方形地四周走了一圈,接着沿着第②块长方形地四周走了一圈,这时走的路程是第一块地的2倍;再沿着第③块长方形地四周走了一圈,这时走的路程又是第一块地的3倍。第④块长方形地的面积与第①块长方形地的面积比是多少?
一名学生列举出这样的策略:
1∶2∶3 = 2∶4∶6 = …… . = 8∶16∶24
8 ÷ 2 = 4 = 3 + 1;16 ÷ 2 = 8 = 7 + 1;24 ÷ 2 = 12 = 9 + 3;9 × 7∶(3 × 1) = 21∶1
从学生的研究过程看,在逐步尝试中,通过有序列举,发现了各部分图形的长与宽之间的关系。
还有个别学生在小组共同研究基础上(需要老师给予一定的帮助),进行了逻辑推理:
解:设长方形①的长X米,宽Y米;第二个长方形宽Y米,长为2(x + y) × 2 ÷ 2 - y = 2x + y;第三个长方形宽x米,长为2(x + y) × 3 ÷ 2 - x=2x + 3y,根据正方形边长相等,可以得到:2x + y + x = 2x + 3y + y,x = 3y,7y × (9y)∶(3y × y) = 21∶1
为了进一步发挥“画图”之作用,让“数形结合”成为学生进行游戏操作手段并有机发展学生的高阶思维,教师借助电脑,设计游戏“动画”,不断分割图形,变通解题思路,引领学生主动发现规律(如图6)。
动画1:将长方形②的长分一分,分成3段,使之等于长方形①的“长 × 2 + 宽”(由周长倍比关系可知,右边的小长方形一定是正方形,想一想:为什么?)。
动画2:将长方形③的长平均分3段,正好等于长方形①的长的3倍(大的正方形边长相等,最右上角的小正方形边长相等),正好满足长方形③的周长是长方形①的周长的3倍。
动画3:将①分成3个完全一样的图形,每个图形一定是正方形(长方形①的长正好是宽的3倍)。
由图可知,长方形④的长是长方形①长的3倍,也就是小正方形状边长的9倍,长方形④的宽是长方形①宽的7(2 × 3 + 1)倍,于是可以得出长方形④与长方形①的面积比是:9 × 7∶ (3 × 1) = 21∶1。
解决问题,既要提倡方法的多样化,又要强调思路的优化。在上面的游戏式分割中,巧妙构建一个小“正方形”,并从不同图形的周长关系出发,将整个图形化作若干个“正方形”单位,让学生的理解建立于直观,深化于推理,变化于求异,从而形成富有创意的思路。
综上所述,深度学习小学数学游戏的应用,应当致力于开发生动的、有意味的游戏,力求形式与内容统一,静态与动态结合,规则与自由制衡,通过创设情境、改变规则、深度体验、对话思辨、变通求异等策略方法,让学生生发“五趣”、深刻理解,放飞思维灵感,灵活解决问题,从而走向“深度学习,游戏共生”的大境界!
[参 考 文 献]
[1]安富海.促进深度学习的课堂教学策略研究[J].课程·教材·教法,2014(11):57-62.
[2]沈君.基于数学理解的游戏教学探析[J].小学数学教与学,2021(4):35.
[3]冯季林.教学的游戏性研究[M].桂林:广西师范大学出版社,2009.
(责任编辑:杨红波)
作者简介:洪建林(1970—),男,江苏如皋人,江苏如皋经济技术开发区实验小学高级教师,大学本科,研究方向:小学数学教育。

