基于改进蚁群算法的四足机器人步态规划*

胡平志，李泽滔

(贵州大学电气工程学院，贵州 贵阳 550025)

1 引言

近年来，随着微型计算机控制技术的完善，各式各样的机器人不断出现，其中适应复杂地形的足式机器人成为研究热门。不同于轮式、履带式和旋翼式机器人，足式机器人关节数量众多，运动方式复杂，其步态规划方式为机器人运动控制的基础。针对机器人步态规划算法，文献[1-3]提出了模仿动物运动的步态规划算法，这类算法具有较好的稳定性，但过分依赖于对动物的观察，适用于特定仿生形态的机器人。这3篇文献的算法分别对应了马(4足)、蚂蚁(6足)以及螃蟹(8足)，与本文所研究的机器人形态和足数均不一样，这些算法难以适应其他形态机器人以及本文所提及的四足机器人。

文献[4-6]提出了基于智能算法的机器人步态规划，这类算法能够较为广泛地适用于不同形态机器人。其中，文献[4]提出了基于智能决策算法的路径规划；文献[5]提出了结合遗传算法的基于零力矩点轨迹规划的四足机器人步态规划；文献[6]提出了基于马尔可夫决策的六足机器人算法，并且还提出了离散化轨迹的分析方法。

基于上述参考文献，本文提出基于改进蚁群算法的步态规划算法，将机器人的4足转化为四维空间坐标，并结合离散化轨迹的方法，将各种步态转化为四维空间内的离散点，从而将抽象的步态规划问题，转化为四维空间里的路径规划问题。值得注意的是，与传统步态规划问题寻求最短路径不同，本文算法的目的是规划一条最长路径，因此需要对传统路径规划算法进行改进。路径规划算法数量众多[7 -16]，常用路径规划算法包括遗传算法、人工势场算法、蚁群算法、迪杰斯特拉算法和模拟退火算法等。考虑到由四足运动步态点转化得到的四维空间中离散点众多，且由于路径相位不同，最优路径不止一条，为了能广泛搜索路径，避免遗漏，本文选择群智算法对四足机器人摆动相步态进行搜索，由于蚁群算法在相关领域发展较为成熟，故本文采用蚁群算法求取最优路径，即最优步态规划。

为了确保机器人能够稳定运行，本文针对所研究机器人讨论了零力矩点控制方案。最后，结合样机实验，证明了由本文算法搜索得到的步态，能够满足本文所针对的机器人。

2 机器人建模

2.1 单机械腿建模

为实现对每个机械足的精确控制，需要对每个机械足进行抽象建模，如图1a所示的一条机械腿可以被抽象成如图1b所示的模型，进而建立如图1c所示的空间直角坐标系。

Figure 1 Robot single-leg modeling图1 机器人单腿建模

通过DH(由Denavit和Hartenberg所提出的一种建立机器人运动学模型的算法)矩阵法[17,18]，对单条腿建立运动学方程，计算化简之后得到的方程组如式(1)所示：

(1)

其中,px,py,pz表示机器人末端点P在直角坐标系中的空间坐标，各参数实际取值如表1所示。

Table 1 Variables of 3-DOF mechanical leg表1 三自由度机械腿变量

表1中,θw为第w关节输出角度,dw为第w关节旋转轴与第w+1关节旋转轴之间沿轴方向距离，aw为第w关节旋转轴与第w+1关节旋转轴之间的法线距离，αw为第w关节旋转轴与第w+1关节旋转轴之间的夹角。由此方程组可以求解运动学逆模型，一条机械腿的运动，实际上就是控制θ1，θ2，θ3从而控制末端点P拟合空间内曲线DE的过程，配合步态控制策略，4条机械腿按照一定的顺序运动，即可以使得机器人做出相应的运动。

2.2 四足机器人逆模型求解

为了有效控制机械腿运动，需要求解逆模型，但是该模型解析解求解困难，以下不加证明地给出一种迭代求解运动学逆模型数值解的方法。为简化计算，模型方程组被转化到圆柱坐标中，由于被转化为圆柱坐标，坐标由(x,y,z)转化为(ρ,θ1,z)，其中ρ=|(x2+y2)0.5|为极轴长度，θ1=arctan(y/x)为极角，同时θ1也是第1关节的输出角，如图2所示。

Figure 2 Rectangular coordinate to polar coordinate图2 直角坐标变换到圆柱坐标

图2中

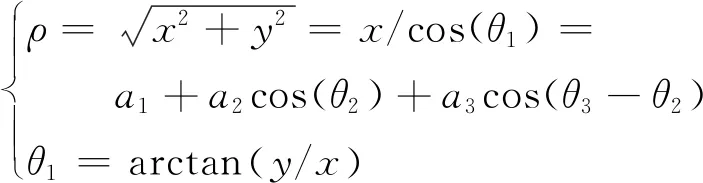
(2)

方程组(1)变化为如式(3)所示:

(3)

由ρ=a1+a2cos(θ2)+a3cos(θ3-θ2)可以直接分解得:

(4)

简记为θ3=g(θ2,ρ)。

利用θ2控制z的变化，并修正由θ3变化带来的偏差Δz，由z=a2sin(θ2)-a3sin(θ3-θ2)变换可得到关于sin(θ2)的一元二次方程a·sin2(θ2)+b·sin(θ2)+c=0，从而可以求解出θ2。

sin(θ2)的一元二次方程相关参数如式(5)所示：

(5)

Figure 3 Topology of quadruped robot图3 四足机器人拓扑图

由一元二次方程求根公式可得sin(θ2)，再利用反三角函数求解出θ2，如式(6)所示：

θ2=arcsin((2z(a2+a3cos(θ3))±

((-2z(a2+a3cos(θ3)))2-4((a2+a3cos(θ3))2+

(6)

将θ2表达式简记为θ2=f(θ3,z)，联立式(3)～式(6)可得到如式(7)所示的迭代式：

(7)

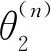
2.3 四足机器人拓扑图

为确定机器人运动策略，需要对机器人做出如图3所示的简化，将机器人抽象为拓扑图。

如图3所示，其中图3a为机器人实物模型三维俯视图，在图3b中，机器人的12个舵机被抽象为12个方格，由于4条腿关于机器人几何轴中心对称，所以将其按照顺时针分为A，B，C，D4个组，每组3个关节，序号由内向外依次从3减小至1。

由文献[6]的启发，将4条机械腿的运动轨迹进行分段，本文主要讨论如图4所示直线行走步态，由于篇幅和主题限制本文暂不讨论轨迹生成问题。

Figure 4 Discretization trajectory图4 离散化轨迹

如图4所示，一条机械腿运动过程被划分为7个阶段，其中阶段1～阶段5，机械足末端点P与地面紧贴为四足支撑相，按照从1～5的顺序拟合一条曲线，到达第5阶段后，抬起机械腿，使得P点脱离地面，到达第6阶段，向前运动到达第7阶段后，放下机械腿，使得P点重新紧贴地面，回到第1阶段。其中，第6和第7这2个阶段为三足支撑，单足摆动相，这2个阶段不直接对机器人运动做出贡献，本文算法仅讨论1～5阶段四足支撑相。其中,A3,B3,C3,D3表示机器人4条腿的第3关节。

由于机器人有4条腿，所以存在一个运动的先后次序，可以看出因为是周期运动，所以ABCD的运动次序与BCDA、CDAB、DABC等运动次序实质上是一致的，只是相位不同，按照循环排列方式，其策略总数如式(8)所示，一共6种方式:

(8)

3 四维空间路径规划

3.1 四维空间建立

因为4条腿的运动本质是相互独立、线性无关的，本文算法利用这一特点，将4条腿运动轨迹，抽象建立为一个四维直角坐标系O-ABCD，如图5所示。

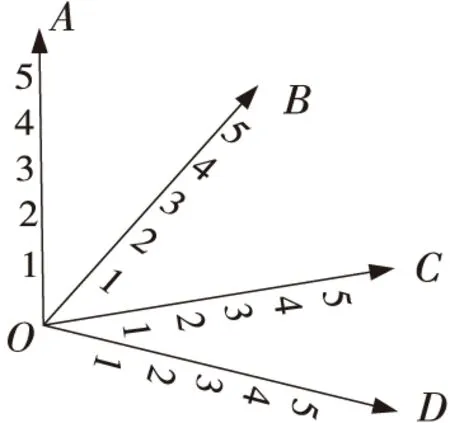
Figure 5 Four-dimensional space coordinate system图5 四维空间坐标系

图5中OA代表A腿的支撑相1～5阶段，OB，OC，OD同理，每个坐标轴只取1～5 这5个离散的整数点，对应4条机械支撑相滑动相的5个步态点。

3.2 适应度函数

规划机器人在一个运动周期中，4条腿的步态可以被视为在O-ABCD坐标系下寻找一个四维坐标序列，使得在该周期里机器人走过的路程最长，即寻找在该空间中的最长路径。在这一定义下，适应度函数如式(9)所示:

(9)

其中,Lt代表第t轮迭代机器人走过的路程总长度，Lt的值为8个步态点之间7个间隔距离Lstep之和，每个间隔距离Lstep又等于机器人从一个状态点转移到下一个状态点之后，4条机械腿位移dleg的总和。

3.3 机器人行走规则

控制机器人行走有如下规则：

(1)为保持机器人运动平稳，任意时刻，机器人至少有3条腿接触地面，作为支撑。

(2)为保证任意一个机械结构不过度磨损，机器人运动时4条腿应同时动作，且动作幅度一致。

(3)为保证机器人快速向某一方向运动，在机械腿紧贴地面的阶段(即阶段1～阶段5)，机械足任意时刻的运动必须与机器人整体运动方向平行且相反。

对于规则(2)，可以引申为任意一条腿只能由第n阶段转移至第n+m阶段，为方便规划，统一定义m=1，即任意一条腿只能由第n阶段转移至第n+1阶段，特别地，第5阶段只能转移至第1阶段。并且应该由4条腿一起驱动使得机器人移动，这也就意味着，当某一条机械腿运动至第5阶段后，由于该机械腿悬空，其余3条腿应该保持原地不动，等待该条腿通过第6、第7阶段回到第1阶段。

对于规则(3)，可以引申为阶段转移只能增加不能减少，特别地，第5阶段只能转移至第1阶段。若出现阶段减少，则引入适当惩罚机制。

由规则(2)和规则(3)可以得到如表2所示规则表。

Table 2 Reward and punishment rule表2 奖励与惩罚规则

由此可以明显看到，奖励方式与机械腿运动对机器人整体运动的贡献有关，即只要能有利于驱动机器人向某一特定方向运动，则该转移方式将得到奖励，特别地由阶段5转移到阶段1，由于只有1条腿运动，需要特殊的奖励方式。

如表2所示，任意一条腿由前一阶段向后一阶段转移，将出现总共25种情形，不同情形对应的奖励g不同。

在本文算法中，奖励模式1对应g=+1，奖励模式2对应g=+4，保持不动对应g=0，惩罚对应g=-10,由此得到转移规则矩阵G,如式(10)所示:

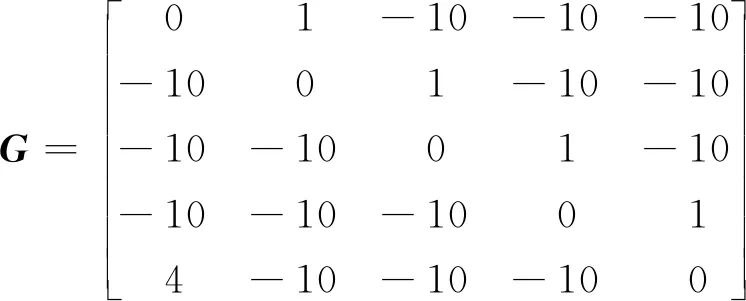
(10)

3.4 改进蚁群算法

第step步的奖励rewardstep为4条腿奖励收益总和，单条腿收益gi,j由转移规则矩阵确定,如式(11)所示，gi,j代表该条腿由第i阶段转移到第j阶段的收益，对应矩阵G第i行第j列元素。

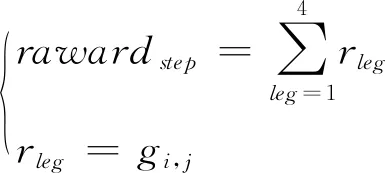
(11)

当rewardstep=4时,说明4条腿都在进行“邻阶段正向转移”,或者只有一条腿在从“第5阶段返回第1阶段”，其余腿均“保持不动”，所以定义第t轮迭代中距离启发函数ηstep(t)如式(12)所示:

(12)

其中，Kd是距离倍率，可以调节启发函数的影响力，Ed为期望值，为使得ηstep(t)得到最大值时，rewardstep的值与期望值Ed接近，应使得|rewardstep-Ed|趋近于0。

结合规则(1)和规则表2，在奖励规则下只有得到分数rewardstep为4才是最优选择，所以选择Ed=4+ε，其中|ε|应远小于1但是大于0。

结合式(11)与适应度函数式(9)可知，距离适应度函数与奖励适应度函数是线性相关的，为便于计算取二者之间系数为1，如式(13)所示:

(13)

值得注意的是，整条路径并不是单纯的rewardstep=4的点的集合，而是这些点按照一定顺序排列得到的结果。

τstep(t+1)=(1-ρ)τstep(t)+Δτstep,

ρ∈(0,1),

(14)

本文算法规划路线为最长路径，相较于传统蚁群算法寻找最短路径有所不同。本文提出的改进蚁群算法流程图如6所示。

Figure 6 Flow chart of improved ant colony algorithm图6 改进蚁群算法流程图

4 仿真结果

本次仿真采用Matlab 2014a在Windows 7系统中运行，仿真迭代初始条件如表3所示，50个个体进行20次迭代，在四维空间中寻找最长路径。

值得注意的是，由于该四维空间内离散点数量众多，但是蚁群总数较少，为避免本文算法陷入局部最优，同时扩大搜索范围，所以每次迭代都会重新随机选择蚂蚁初始位置，以增加样本数量。

如图7所示，图中纵轴是单次迭代路程的平均值，在20轮迭代后，路径长度逐渐收敛于(1000,1200)，之所以无法收敛于某个固定值，是由于每次迭代初始位置是随机的，不论迭代多少次，都会随机出现非最优解，从而导致最终的结果总是存在随机波动。尽管如此可以看出该平均值依然是收敛的，经过多次迭代仿真，结果依然收敛，其中5次迭代仿真结果如图8所示。

Table 3 Initial condition of iteration表3 迭代初始条件

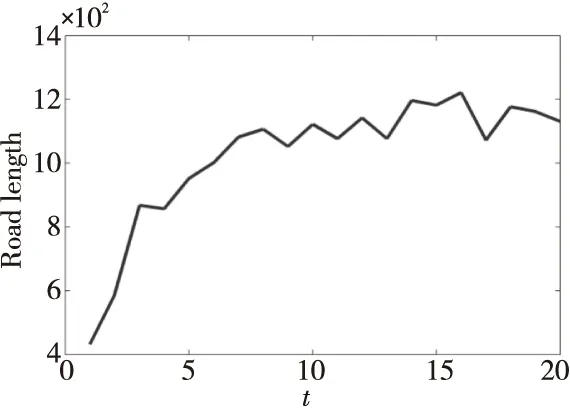
Figure 7 Iterative convergence of the algorithm图7 算法迭代收敛

Figure 8 Convergence after multiple iteratios图8 多次迭代收敛

经过多次仿真实验得到如式(15)所示6组4足支撑相控制规则矩阵，符合之前的分析。由第1行可以看出，每一组之间只是列的顺序不同，即4条腿的运动先后次序不同，符合式(8)的预期。

(15)

5 零力矩点控制

因为腿从阶段5返回到阶段1需要经过阶段6和阶段7位置摆动相的变换，所以仍然需要扩充式(15)所示矩阵。

同时如图9所示，黑色圆形A、B、C、D代表与地面直接接触做支撑的腿，虚线圆形A代表摇摆相时抬起的腿，以A腿抬起为例，虚线圆形M代表机器人的重心，虚线框代表支撑面。在支撑相时四足做支撑，此时重心M落在支撑面四边形ABCD上，所以机器人可以稳定站立。但是在摇摆相时，抬起A腿后，支撑面由四边形ABCD变为三角形BCD，重心M落在支撑面BCD之外，这使得摇摆相时机器人将出现站立不稳进而跌倒的现象。为解决这一问题，则需要另外3条腿做出相应调整，使得机器人在一条腿处于摇摆相时，重心重新落在由其余3条腿构成的支撑面内，如图10所示。

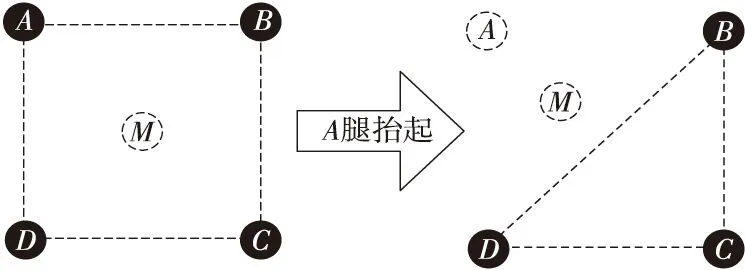
Figure 9 Gravity center movement in swing phase图9 摆动相重心偏移

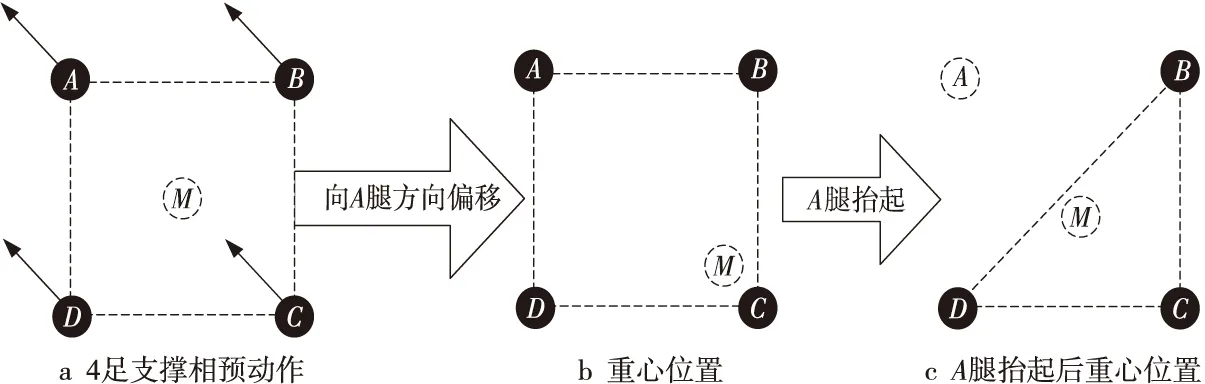
Figure 10 Correction for gravity center movement in pre-action图10 预动作修正重心偏移

在A腿抬起之前，4条腿向CA连线方向偏移(如图10a所示)，使得重心M向AC方向偏移，落在三角形BCD内(如图10b所示)，最后A腿再抬起来(如图10c所示)。这样才能符合零力矩点控制，使得机器人稳定运行。由此，在机器人单腿抬起摆动之前，需要再添加一个如图10a所示的预动作步态，以式(15)中第1个矩阵为例进行详细论证，式(15)中第1个矩阵加入预动作后的扩展规则表如表4所示。其中，步态1～步态3、步态6～步态8、步态11～步态13、步态16～步态18为支撑相；特别地，步态1与步态2、步态6与步态7、步态11与步态12、步态16与步态17时4条腿同时驱动机器人沿直线向前运动；步态3、步态8、步态13、步态18为预动作，此时4腿支撑且发生偏移，为接下来摆动相保持平稳做准备；步态4、步态5、步态9、步态10、步态14、步态15、步态16、步态19、步态20为摆动相，此时除了抬起的那一条腿摆动到阶段6和阶段7外，其余腿均保持在支撑相预动作阶段，以维持机器人3足支撑的稳定性。

Table 4 Extended rule 表4 扩展规则

表4中“*”表示需要调整位置，当第i条腿抬起时，第j条腿末端点P坐标由(xj,yj)调整为(Xj,Yj)的规则如式(16)所示:

(16)

该规则表示末端点P坐标沿直线(Yj-yj)=k(Xj-xj)由(xj,yj)移动距离l到(Xj,Yj)。由于是一个二元二次方程组，则必然存在4个解，如式(17)所示：

(17)

其中,k为方向系数，这里取k=1，kxi,j与kyi,j为符号系数，取值为±1，i为抬起腿的序号，j为放下腿的序号，这些参数决定了其余3条腿的偏移方向，同时取l=20 mm，l决定了偏移的距离，其中kxi,j与kyi,j的取值规则如图11所示。

Figure 11 ZMP controlling topology图11 ZMP控制拓扑图

如图11a所示，点P的偏移方向根据kxi,j与kyi,j的取值，一共有4种方式，如表5所示。

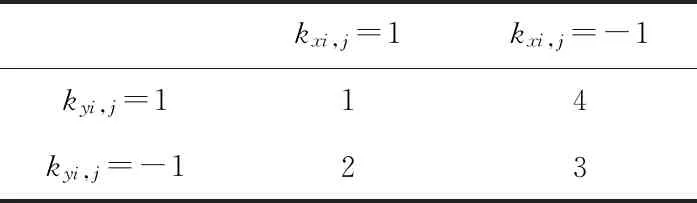
Table 5 Movement directions 表5 偏移方向

但是，如图11b所示，以A腿离开地面，BCD作支撑为例，当A腿离开地面后，重心会向A偏移，为平衡这一偏移，其余3足应沿着箭头A方向运动，但是由于机器人的重心对称特性，每一条足运动坐标变化方向均不一样，以B腿为例：B腿末端点x坐标应减小，y坐标应增大，即对应kxi,j=-1，kyi,j=1，对应方向4；同理，C腿偏移方向为3，D腿偏移方向为2，A在预动作时偏移方向为1。由此可以得到偏移控制规则如表6所示。

Table 6 Movement control rules table表6 偏移控制规则表

表6中，数字1～4为表5中偏移方向代号，“预”代表本次偏移只在预动作时有效。将表6与表4结合即可以控制机器人运行。以表4中步态4为例，此时D腿抬起，所以A腿在表4中步态2的基础上向4方向偏移，B腿在表4中步态3的基础上向3方向偏移，C腿在步骤点4的基础上向2方向偏移。

6 样机测试

本次实验样机机体结构采用3D打印建造，材质为PLA(聚乳酸)，采用TS-315总线数字舵机作为伺服系统，可同时采用stm32嵌入式做脱机控制，或者采用PC机数据线做在线控制。本次测试采用PC机数据线做在线控制，机器人样机如图12所示。

为标定机械足顺序，将其中一只采用黄色材料打印，由于图片转为灰度图，图中颜色应为浅灰色。左上方浅色的腿为B，沿顺时针方向依次为BCDA，由前文可知该运动方式等效于ABCD运动方式。该机器人按照表4所示规则，运行20步行走100 mm的录像截图如图13所示。

Figure 12 Robot prototype 图12 机器人样机

Figure 13 Video capture of robot prototype walking图13 机器人样机行走录像截图

经过10次实验，得到数据取平均值，与设置值的对比如表7所示。

Table 7 Comparison of experimental data表7 实验数据对比

由于实际测量工具最小分度值为毫米(mm)和度(°)，存在较大误差，所以平均值全部保留整数。由于未作防滑处理，机器人在地面行走时难免出现打滑，之后应在机器腿末端做防滑处理。

如图13所示，前2列为本文算法搜索出来的驱动机器人前进的8个步态，直接驱动机器人前进；第3列为偏移重心的预动作，为摇摆相时机器人的平衡做准备；前3列为4足支撑相，第4列和第5列为摇摆相，使得处于末位5的腿重新摆回初始位1。从1到20分别对应20个步态，机器人从右往左沿直线运动，整个过程中，机器人重心平稳，运行稳定，符合本文设定的机器人行走标准。

7 结束语

本文针对四足机器人的特性，将四足步态规划问题转化为四维空间中需求最长路径问题，并改进蚁群算法，将搜寻最短路径转化为搜寻单位时间内的最长路径。并针对四足机器人在水平地面上直线行走步态规划进行了研究。在多次仿真模拟中，从2.28×1010种步态组合中搜索出了24种符合约束条件的步态，表明了本文算法的有效性和快速性。得到基础的8个步态后，根据零力矩点控制对矩阵扩充，有效解决了重心不稳的问题，进一步优化了机器人运行的稳定性。最后通过程序控制样机测试，机器人样机在地面上稳定行走，未出现摇晃和明显偏移，从而验证了本文算法的实用性。