T型过渡圆弧长度对铁路车轴疲劳性能的影响研究
杨凯,史玉杰,李亚波,刘为亚,陈一萍,董懿辉,鲁连涛
T型过渡圆弧长度对铁路车轴疲劳性能的影响研究
杨凯1,史玉杰1,李亚波1,刘为亚1,陈一萍1,董懿辉2,鲁连涛2
(1.中车青岛四方机车车辆股份有限公司工程实验室,山东 青岛 266111;2.西南交通大学 牵引动力国家重点实验室,四川 成都 610031)
研究了非动力车轴T型过渡圆弧长度对车轴轮座微动参量,微动疲劳SWT参数和过渡圆弧最大主应力的影响,并根据EN 13103-2017校核了车轴过渡圆弧设计的合理性。研究发现:车轴轮座接触压应力、摩擦剪切应力随着的增加而减小,轴向滑移幅值随着的增加而增加。微动疲劳SWT参数随着增加而增加,减小可以缓解车轴微动疲劳损伤。针对该研究车轴,当由35 mm增至42 mm时,T型过渡圆弧处最大主应力先减小,此后几乎不变,最大值位置由两段圆弧内切点向轴身侧转移。仿真计算得到的min略小于标准建议值,车轴设计满足EN 13103-2017对车轴过渡圆弧设计的要求。
过渡圆弧;微动参量;SWT参数;最大主应力
车轴是铁路轮轴系统重要的组成部分,关系到列车的安全运行[1]。车轴一旦发生疲劳失效,将可能造成列车脱轨等严重的安全事故。车轴和车轮采用过盈配合方式连接,在疲劳载荷作用下,轮轴配合边缘由于往复的微小滑移可能引发微动疲劳[2-4]。此外,车轴也可能由于设计不优等引入的应力集中引发轴身疲劳[5]。
标准建议非动力车轴轮座与轴身间采用半径为15 mm和75 mm两段圆弧内切进行过渡,且轮座与轴身的直径比/≥1.12[6]。如图1(c)所示,车轴过渡圆弧由圆弧半径和过渡圆弧长度共同确定。但是,目前国内标准只给出了的建议取值,这导致设计人员难以确定合理的过渡圆弧长度。此前,学者们针对过渡圆弧尺寸进行了大量工作:Nishioka等[7-8]采用比例车轴研究了过渡圆弧对车轴微动疲劳的影响,发现微动疲劳强度随过渡圆弧半径的增大而减小;张进德等[9]在实际车轴疲劳试验中获得了相似的结论;杨广雪等[10]基于有限元研究了实际车轴过渡圆弧半径对轮座配合面接触压应力的影响,发现过渡圆弧半径越大,接触压应力越大。上述研究表明,车轴过渡圆弧的尺寸会影响车轴轮座微动参量的分布及微动疲劳强度。然而,尚无学者研究对车轴轮座微动疲劳性能的影响。
过渡圆弧的形状除了对车轴轮座微动疲劳产生影响外,还可能影响车轴轴身疲劳。Cervello[5]采用实际车轴疲劳试验研究了的取值对轴身疲劳的影响,发现的不同取值会影响轴身疲劳抗力。Traupe等[11]基于实际车轴仿真研究了不同对车轴过渡圆弧应力分布的影响,研究发现的最小取值须保证过渡圆弧处的最大主应力不出现在两段圆弧内切点,依据大量的计算给出了车轴的最小尺寸计算公式,且该式有效性得到实际车轴试验验证。此后,欧洲标准将该研究成果纳入最新车轴设计标准EN 13103-2017[6]中。显然,已经成为车轴设计的重要参数。国内高速铁路非动力车轴设计之初,并没有考虑的取值对车轴疲劳性能的影响。因此,有必要根据EN 13103-2017对车轴过渡圆弧设计的合理性进行校核。
本文以某国产高速铁路非动力车轴为例,建立有限元模型,仿真研究了不同过渡圆弧长度对车轴轮座微动参量,微动疲劳参数及过渡圆弧最大主应力分布的影响。此后,依据EN 13103-2017对该车轴过渡圆弧设计的合理性进行校核。
1 研究对象
1.1 车轴形状与尺寸
本文选用某国产高速铁路非动力车轴进行研究。为了便于后续仿真分析,本文参考Traupe等[11]的研究,将车轴在Minden型轮轴疲劳试验台上试验的试样形状、边界条件及载荷作为输入条件。车轴试样如图1所示,压装过盈量取0.243 mm,约为车轴轮座直径的1.22‰,符合标准EN 13260[12]对轮轴间过盈量的规定。

1.2 材料参数
仿真时车轴材料选用EA4T车轴钢,车轮材料选用ER8车轮钢。车轴和车轮材料的力学参数如表1所示。

表1 材料力学参数
2 有限元仿真
2.1 有限元模型
根据图1所示试样的形状尺寸建立全尺寸车轴有限元模型,单元类型为八节点六面体完全积分单元(C3D8)。整个模型分为车轴和车轮两部分,有限元模型如图2所示。由于本文研究对车轴轮座微动疲劳损伤及过渡圆弧最大主应力分布的影响,对轮座边缘及过渡圆弧的网格进行细化,最小网格尺寸为0.05 mm,以便于捕捉复杂的应力变化。以=39 mm模型为例,模型网格数共347,120个、节点数共386,160个。车轴与车轮间的过盈配合接触采用接触对的形式建立,车轮轮毂内孔面为主面,车轴的轮座面为从面。接触面间的摩擦遵循库仑定律,轮轴配合面间的摩擦系数取0.7[13-15],接触行为由罚函数接触算法控制,最大弹性滑移容差取0.0001。
仿真模型采用线性随动硬化模型来考虑轮座边缘由接触引起的塑性变形。则有EA4T车轴钢的屈服应力σ和硬化模量分别为552 MPa和5.4 GPa,ER8车轮钢的屈服应力σ和硬化模量分别为584 MPa和8.0 GPa。
本文有限元模型中的边界与加载条件设置如下。在车轮表面施加固定约束,车轮左侧面施加方向约束,这样来模拟Minden型台架试验的边界条件。通过在加载部位施加随时间呈三角函数变化的循环载荷,实现与车轴旋转等效的旋转弯曲载荷。分别沿和轴施加两个相互垂直的分力载荷,两个载荷的幅值相同,初始相位差90°,这样就可以实现两个分力的合力沿对称轴旋转的效果。施加的载荷大小使得轮座边缘名义弯曲应力为100 MPa。

图2 有限元模型
2.2 仿真工况
相关标准推荐,过渡圆弧由半径分别是有15 mm和75 mm的两段圆弧共同组成[6]。实际车轴参考标准UIC 515-3,建议过渡圆弧的最小长度为min=35 mm[11],但并没有规定车轴过渡圆弧的最大长度。根据画法几何,图1所示车轴过渡圆弧最大尺寸可以取max=42 mm。
因此,本文研究选用的是在35~42 mm内取值,分别为35 mm、37 mm、39 mm、41 mm和42 mm。值得注意42 mm时过渡圆弧即为=75 mm的单圆弧。
2.3 评估参数
2.3.1 微动疲劳
车轴轮座处受到以轴向应力和剪应力为主的多轴应力作用,故采用多轴疲劳分析模型结合临界平面法研究车轴轮座微动疲劳问题[16]。学者们普遍认为Smith-Waston-Topper(SWT)参数法[17]可以对车轴轮座微动疲劳进行有效评估,即认为疲劳破坏是由临界平面上的最大法向应变幅值及最大法向应力共同导致。
计算公式为:


数值越大,微动疲劳损伤越严重。
2.3.2 轴身疲劳
Traupe等[11]将不同的车轴直径比以及过渡圆弧长度和半径等结构参数相组合,并采用商业有限元软件ABAQUS建立了8,880个对应的有限元模型,研究了车轴结构参数的变化对过渡圆弧最大主应力分布的影响。研究发现,车轴设计需要保证过最大主应力不出现在两段圆弧内切点。
Traupe等[11]对仿真计算的数据进行处理,得到了过渡圆弧最小长度min为:
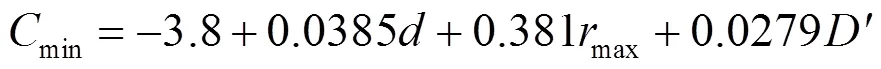
式中:为车轴计算应力集中位置的直径,mm;max为过渡圆弧中数值较大的圆弧半径,mm;为轮毂直径,mm。
在本研究中,取=170 mm、max=75 mm、=252 mm,则可以计算得到该车轴的min=38.4 mm。
3 结果与讨论
3.1 微动参量
以往的研究表明,有50个以上的微动参量会对机械结构的微动疲劳产生影响,这些参量在机械结构的微动疲劳进程中交互作用[18-19]。对于铁路车轴而言,接触压应力、摩擦剪切应力和滑移幅值是最重要的微动参量,因此本文将研究非动力车轴T型过渡圆弧长度对车轴轮座微动区的接触压应力、摩擦剪切应力和滑移幅值这几个微动参量的影响。在旋转弯曲载荷作用下,车轴受拉侧相较于受压侧更容易发生疲劳失效,因此本文的微动参量均取自车轴受拉侧。
3.1.1 接触压应力
图3为不同对轮座配合区域接触压应力分布的影响。由(a)可以看出,接触压应力的最大值均出现在轮座边缘,各评估位置接触压应力随着距轮座边缘距离的增加而减小。的取值会影响距轮座边缘-2~0 mm范围内接触压应力的分布,而远离轮座边缘配合区域的接触压应力几乎不受的影响。由(b)可以看到,当<41 mm时接触压应力随着的增加而减小,当=42 mm时接触压应力会迅速增大。本文出现这一现象是因为=42 mm时过渡圆弧为=75 mm的单圆弧。
3.1.2 摩擦剪切应力
图4为不同对车轴轮座配合区域摩擦剪切应力分布的影响。摩擦剪切应力与图3接触压应力的分布规律完全一致,只是数值上有所差异。这是因为本节中接触压应力和摩擦剪切应力均取自车轴滑移区,此时摩擦剪切应力的大小由接触压应力和库伦摩擦系数决定。
3.1.3 轴向滑移幅值
服役的铁路车轴在循环弯曲载荷作用下轮轴配合面会发生往复的微小滑移。一般来说,轴向滑移幅值越大,轮轴间的微动行为越剧烈,车轴也就越容易产生微动损伤。图5为不同对轮座配合区域轴向滑移幅值分布的影响。由(a)可知,轴向滑移幅值的最大值均出现在轮座边缘,随着评估位置向轮座内部移动,轴向滑移幅值逐渐减小,这是因为越靠近轮座内部,轮轴间的配合越紧密。对于滑移区内任一评估位置,轴向滑移幅值都随着的增加而增加。由(b)可知,最大轴向滑移幅值随着的增加而增加。
综上,可以看到车轴微动区的接触压应力、摩擦剪切应力和轴向滑移幅值会在不同程度上受T型过渡圆弧长度的影响。相较于接触压应力和摩擦剪切应力,轴向滑移幅值受到的影响更大,这说明的取值会显著影响轮轴间的微动行为。

图3 不同C对接触压应力的影响

图4 不同C对摩擦剪切应力的影响
3.2 微动疲劳SWT参数
图6为不同对车轴轮座微动疲劳参数分布的影响。由于轮座边缘严重的应力集中,参数最大值均出现在轮座边缘。在距轮座边缘-0.4~0 mm的范围内,参数值随着距轮座边缘距离的增加而迅速下降,而远离轮座边缘配合区域的参数值则几乎不受的影响。
参数最大值表征车轴微动疲劳损伤。图6(b)则是不同对参数最大值的影响,可以看出参数的最大值随着的增加而增加,且当值由41 mm增加至42 mm时,参数值急剧增大。这是因为本文中,前四种过渡圆弧均由=15 mm和=75 mm两段圆弧内切组成,而=42 mm过渡圆弧采用=75 mm的单圆弧。结合图3~5可知,当仅采用=75 mm的单圆弧过渡时,轮座边缘的应力集中难以得到充分缓解,轮轴间微动行为更剧烈,这使得参数急剧增大。图6(b)表明车轴微动疲劳损伤随着的增加而增加,为了尽可能缓解车轴轮座的微动疲劳,建议在车轴设计中选用较小的值来减小微动疲劳损伤。

图5 不同C对轴向滑移幅值的影响

图6 不同C对SWT参数的影响
3.3 过渡圆弧最大主应力
对于非动力车轴T型过渡圆弧,车轴轮座与轴身间多采用=75 mm和=15 mm圆弧进行过渡,这势必会引入应力集中,从而导致该部位成为车轴设计的危险部位。Traupe等[11]建议采用最大主应力对车轴过渡圆弧应力分布进行评估,因此本文在仿真计算后取圆弧处最大主应力进行分析。
图7(a)为不同对车轴T型过渡圆弧最大主应力分布的影响,可以看出,最大主应力在过渡圆弧靠近轮座侧存在峰值P、在过渡圆弧靠近轴身侧存在峰值P。随着增加,峰值P逐渐减小、位置向轮座侧移动,峰值P基本不变、位置向轴身侧移动。图7(b)为各过渡圆弧最大主应力最大值及其位置随的变化,可以看到当过渡圆弧长度由=35 mm增至=37 mm时,最大主应力急剧减小(由峰值A转移至P),最大值位置向轴身侧转移,此后随着过渡圆弧长度由=37 mm增加至=42 mm,最大主应力基本不变(峰值P),最大值位置继续向轴身侧移动。
Traupe等[11]认为,当T型过渡圆弧的最大主应力出现在两段圆弧(=15 mm和=75 mm)内切点时,车轴容易由于轴身处的应力集中出现轴身疲劳,因此车轴设计应保证最大主应力位置不出现在两段圆弧内切点。根据该评估准则,结合图7计算结果可知,该车轴的最小过渡圆弧长度取37 mm,略小于2.3.2节计算得到的min=38.4 mm。

图7 不同C对过渡圆弧最大主应力的影响
综合前述分析,车轴轮座微动疲劳损伤随的增加而增加,尽可能取较小的来缓解车轴轮座微动疲劳。车轴轴身疲劳则随的增加得到缓解,根据仿真结果的取值存在最小值。这说明车轴轮座微动疲劳与T型过渡圆弧处的轴身疲劳间存在竞争关系,车轴设计应选择合适的来同时保证车轴轮座和轴身的疲劳强度,从而使整个车轴结构达到最优。
通过上述有限元计算及相关分析,可以给出本次所研究的车轴过渡圆弧长度的取值范围为37~41 mm。该车轴在实际应用中的过渡圆弧长度=40 mm,满足目前最新的车轴设计标准EN 13103-2017对车轴T型过渡圆弧设计的要求。
4 结果与结论
本文采用有限元研究了车轴T型过渡圆弧长度对车轴轮座微动参量,微动疲劳参数和过渡圆弧最大主应力的影响,并根据EN 13103-2017对车轴过渡圆弧设计的合理性进行了校核。得到如下结论:
(1)会影响车轴轮座微动区接触压应力,摩擦剪切应力和轴向滑移幅值的分布。当采用=75 mm和=15 mm的圆弧过渡时,接触压应力、摩擦剪切应力随着的增加而减小;当仅采用=75 mm圆弧过渡时,接触压应力、摩擦剪切应力相较于两段圆弧时有明显区别。轴向滑移幅值随着的增加而增加。
(2)车轴轮座微动疲劳参数随着增加而增加,减小可缓解车轴微动疲劳损伤。
(3)针对该研究车轴,当由35 mm增至42 mm时,T型过渡圆弧处最大主应力先减小,此后几乎不变,最大值位置由两段圆弧内切点向轴身侧转移。仿真计算得到的min略小于标准值,车轴设计满足EN 13103-2017对过渡圆弧设计的要求。
[1]兰清群. 窄轨客车转向架轮轴疲劳强度及紧固度分析评估[J]. 机械,2016,43(4):55-61.
[2]HIRAKAWA K,KUBOTA M. On the fatigue design method for high-speed railway axles [J]. Proceedings of the Institution of Mechanical Engineers Part F Journal of Rail & Rapid Transit,2001,215(2):73-82.
[3]HIRAKAWA,TOYAMA,KUBOTA. The analysis and prevention of failure in railway axles [J]. International Journal of Fatigue,1998,20(2):135-44.
[4]ZOU L,ZENG D,LI Y,et al. Experimental and numerical study on fretting wear and fatigue of full-scale railway axles [J]. Railway Engineering Science,2020,28(4):365-81.
[5]CERVELLO S. Fatigue properties of railway axles:New results of full-scale specimens from Euraxles project [J]. International Journal of Fatigue,2016(86):2-12.
[6]Railway applications – wheelsets and bogies – non powered axles – design method:EN 13103[S].
[7]NISHIOKA K,KOMATSU H. Researches on Increasing the Fatigue Strength of Press-Fit Shaft :4th Report,Geometry of the End of Press-Fitting and σw1 [J]. Bulletin of JSME,1972,15(87):1019-28.
[8]NISHIOKA K,KOMATSU H. Researches on Increasing the Fatigue Strength of Press-Fitted Shaft Assembly [J]. Bulletin of JSME,1967,10(42):880-9.
[9]张进德,曹志礼. RD_2型实物车轴疲劳试验报告[J]. 铁道车辆,1987,(5):3-11,52.
[10]杨广雪. 高速列车车轴旋转弯曲作用下微动疲劳损伤研究[D]. 北京:北京交通大学,2011.
[11]TRAUPE M,LANDABEREA A. EURAXLES – A global approach for design,production and maintenance of railway axles: WP2 – development of numerical models for the analysis of railway axles [J]. Materialwissenschaft und Werkstofftechnik,2017,48(7):687-98.
[12]Railway applications - wheelsets and bogies - wheelsets - product requirements:EN 13260 [S].
[13]袁才钦,李亚波,杨凯,等. 铁路车轴过盈配合面微动损伤分析及有限元仿真[J]. 摩擦学学报,2020,40(4):520-530.
[14]ZHU C,HE J,PENG J,et al. Failure mechanism analysis on railway wheel shaft of power locomotive [J]. Engineering Failure Analysis,2019(104):25-38.
[15]SONG C,SHEN M X,LIN X F,et al. An investigation on rotatory bending fretting fatigue damage of railway axles [J]. Fatigue & Fracture of Engineering Materials & Structures,2013,37(1):72-84.
[16]ZENG D,ZHANG Y,LU L,et al. Fretting wear and fatigue in press-fitted railway axle:A simulation study of the influence of stress relief groove [J]. International Journal of Fatigue,2019(118):225-36.
[17]SMITH K N,WATSON P,TOPPER T H. A stress-strain function for the fatigue of metals [J]. Journal of Materials,1970,5(4):767-78.
[18]宋川,刘建华,彭金方,等.接触应力对车轴钢旋转弯曲微动疲劳寿命的影响[J]. 材料工程,2014(2):34-38.
[19]周前国. 690合金材料的微动磨损特性研究[J]. 机械,2010(3):78-80.
Impact of the Length of T-Shaped Transition on Fatigue Behavior of Railway Axles
YANG Kai1,SHI Yujie1,LI Yabo1,LIU Weiya1,CHEN Yiping1,DONG Yihui2,LU Liantao2
(1.Engineering Laboratory, CRRC Qingdao Sifang Co., Ltd., Qingdao 266111, China;2.State Key Laboratory of Traction Power, Southwest Jiaotong University, Chengdu 610031, China)
The influence of the T-shaped transition lengthof the non-powered axle on the fretting parameters, SWT parameter and the maximum principal stress were investigated. Then, the transition design was checked according to EN 13103-2017. It was found that the contact pressure and frictional shear stress decreased with an increase of, and the axial slip range increased with an increase of. SWT parameter increased with an increase of, and reducingcan alleviate fretting fatigue damage of the axle. Whenincreased from 35 mm to 42 mm, the maximum principal stress at the T-shaped transition first decreased, and then almost remained unchanged. The position of the maximum value shifted from the inner tangent point of the two radii to the side of the axle body. Themincalculated using FE simulation was slightly smaller than that obtained by EN 13103-2017, and the axle design met the requirements of EN 13103-2017 for the transition design.
transition;fretting parameter;SWT parameter;maximum principal stress
U270.1
A
10.3969/j.issn.1006-0316.2021.11.007
1006-0316 (2021) 11-0049-08
2021-04-28
牵引动力国家重点实验室自主研究课题重点项目(2018TPL_Z01);国家自然科学基金(51375406)
杨凯(1988-),男,山东临沂人,硕士,工程师,主要研究方向为车轴疲劳与断裂,E-mail:yangkai@cqsf.com。

