高雷诺数低温风洞内传热特性数值研究

高鑫宇，聂旭涛，蔡清青，张伟

高雷诺数低温风洞内传热特性数值研究

高鑫宇，聂旭涛，蔡清青，张伟

（中国空气动力研究与发展中心，四川 绵阳 621000）

低温风洞的超音速及其高雷诺数工况下的换热特性是分析低温风洞组件温度场分布的关键因素。对超音速及高雷诺数工况换热特性进行数值模拟，通过采用恢复温度修正传热系数的方法，并且与Dittus-Boleter（D-B）公式和Gnielinski公式的计算结果进行对比分析。结果显示，采用恢复温度修正后的D-B公式和Gnielinski公式在超音速及其高雷诺数工况下仍然具有较高准确性。最后将喷管段实际模型工况数值模拟结果与理论预测值进行对比分析，进一步验证了在温度分布不均匀时采用D-B公式和Gnielinski公式求得的平均换热系数在工程计算中的可行性，以及使用恢复温度修正传热系数计算公式的有效性。

低温风洞；高雷诺数；超音速；换热特性；恢复温度

随着空气动力学的飞速发展，对作为试验设备的风洞有了更高的要求。目前常规风洞已经无法完成雷诺数高于50×106的试验要求，而低温风洞[1]通过降低气流温度的方法达到提高风洞雷诺数模拟的目的，已经成为目前实现高雷诺数模拟的最佳方案。由于液氮在低温工质中廉价和安全，汽化后可迅速吸收大量热量从而喷射液氮，成为目前低温风洞中实现风洞空气回路快速降温的主要途径。目前，世界上两座大型的跨声速低温风洞——美国国家跨声速风洞（NTF）和欧洲跨声速风洞（ETW）均采用液氮工质制冷实现低温运行[2-3]。低温风洞在运行过程中，低温流体在风洞中快速流动，通过对流换热与风洞中的结构建立热平衡，从而实现低温实验条件，气流温度甚至最低可达到90 K[4]，在这样低的气流温度下，整个风洞的雷诺数很高，可达到108量级，使得气流与风洞的对流换热剧烈，由于热胀冷缩的作用，对风洞各部件的安全性和密封性提出了更高的要求。为保证风洞的安全运行，需要对风洞传热进行全面的计算分析，尤其是风洞处于高雷诺数和超音速时的换热特性。

国内外对高速流动换热特性进行了研究。文献[5]在对高速喷管内部的对流换热计算方法进行研究时，采用绝热壁面温度（恢复温度）求解对流换热系数。文献[6]在进行高速平板边界层的对流换热研究时，引入了恢复温度求解对流换热系数。文献[7]在研究收敛扩张喷管湍流边界层的热量测量方法时，引入了恢复温度的概念。

本文采用Fluent软件对高雷诺数及其超音速工况下的管内流动对流换热进行研究，引入恢复温度的概念进行对流换热求解，并与管内对流换热公式进行了对比验证。此外，对风洞收缩喷管段模型换热系数进行模拟求解，与管内流动强制对流换热经验公式进行对比分析。验证了管内流动在引入恢复温度修正后的可行性和准确性，并且验证了D-B公式在雷诺数为107的量级也是适用的。

1 对流换热系数的求解方法

对于管内流动对流换热系数主要通过CFD数值模拟和经验公式两个方面进行求解。

1.1 CFD数值模拟

换热系数的求解公式[8]如下：

式中：q为对流换热热流密度，W/m2；T、T分别为物体表面和流体的温度，K；为对流换热系数，W/(m2·K)。

式（1）适用于低速流体，当流体速度很高时则要考虑粘性流体摩擦引起的温升，即[9-10]：

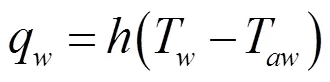
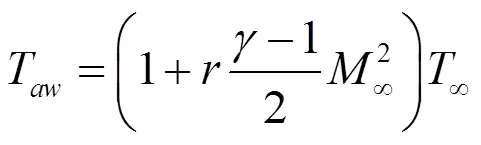
式中：T为壁面恢复温度，K；为恢复系数，其物理意义为绝热壁面由摩擦而引起的温升与高速气体驻点的绝热温升之比；为流体比热比，无量纲；∞为流体主流温度，K；∞为流体主流流动马赫数，Ma。

当∞为无穷小时T＝∞，高速流体的公式与低速流体的公式完全吻合。

层流时[6]，有：

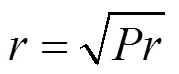
湍流时[6]，有：

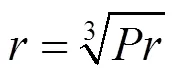
式中：为普朗特数。

用CFD数值模拟求解换热系数，在给定恒定固体壁面温度时，可通过CFD求解出流体与壁面的热流密度，并通过式（3）求解出T，进而通过式（2）求解出换热系数。

本文使用Fluent软件进行CFD数值模拟，选用湍流模型、标准壁面函数，求解方式采用压力基SIMPLE进行求解，流体物性采用NIST物性数据库。

1.2 采用经验公式求解换热系数

根据相关研究[3]影响对流换热系数的主要因素可定性地用函数形式表示为：

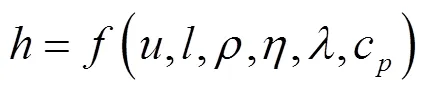
式中：为流体流动速度；、、、、c为几何结构换热表面的特征长度、密度、粘度、导热系数和定压比热。

在低温风洞中流体高速流动，主要涉及的换热类型是管内流动强制对流换热，而常用管内流动强制对流换热经验公式有Dittus-Boelter（D-B）公式和Gnielinski方程。

D-B方程[8]为：

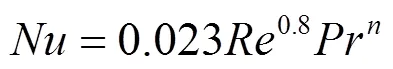
式中：当流体被加热时取0.4，当流体被冷却时取0.3；＞10000。

该经验公式一般要求≥10（其中：为流体管道直径，m；为流体流动管长，m）。

当/＜10时，需要考率入口效应，工程上常采用的入口效应修正系数为[9]：

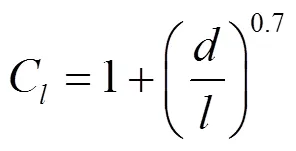
Gnielinski方程为：

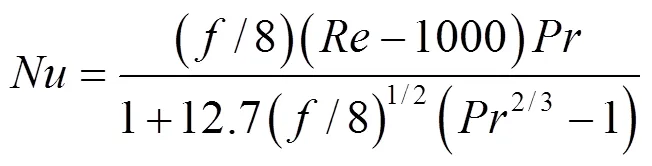
其中：

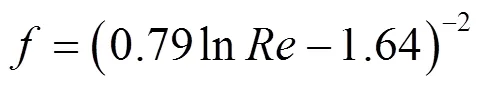
从图1可以看出D-B公式和Gnielinski公式在104～108范围内整体吻合得很好，在106.5～108范围，D-B公式的值较大，但目前两个公式的实验验证范围还没有达到107～108量级。但当风洞处于高压及高速流动甚至风速在实验段达到超音速时，管内流动的雷诺数可以达到107～108这个量级。本文通过Fluent进行数值模拟分析并通过与常用管内流动经验公式进行对比分析，给出一个可以预测风洞处于高雷诺数时强制对流换热可应用的经验公式。

2 数值模拟

为了验证CFD数值模拟的正确性，本文通过外掠平板换热系数结果进行验证。本文在进行数值模拟过程中取板的特征长度为1 m，氮气温度为200 K，压强为1 bar，平板温度取恒定壁温220 K，材料为不锈钢。边界条件为：进口采用速度进口，出口采用流量出口，平板采用恒定壁温，无滑移，其余壁面采用绝热，无滑移。图2为流体外掠平板的温度分布，可以看出平板表面的热边界层厚度逐渐增厚，这符合热力学一般现象。

图2 平板温度分布

这里定性温度按210 K取，物性参数采用NIST REFPROP数据库。

从图3可看出，Fluent仿真结果和解析解吻合得很好，并且误差较小，因此可以采用CFD方法在给定恒定壁面温度边界条件，通过求解固体壁面和流体间换热的热流密度，从而对低温流体求解换热系数。

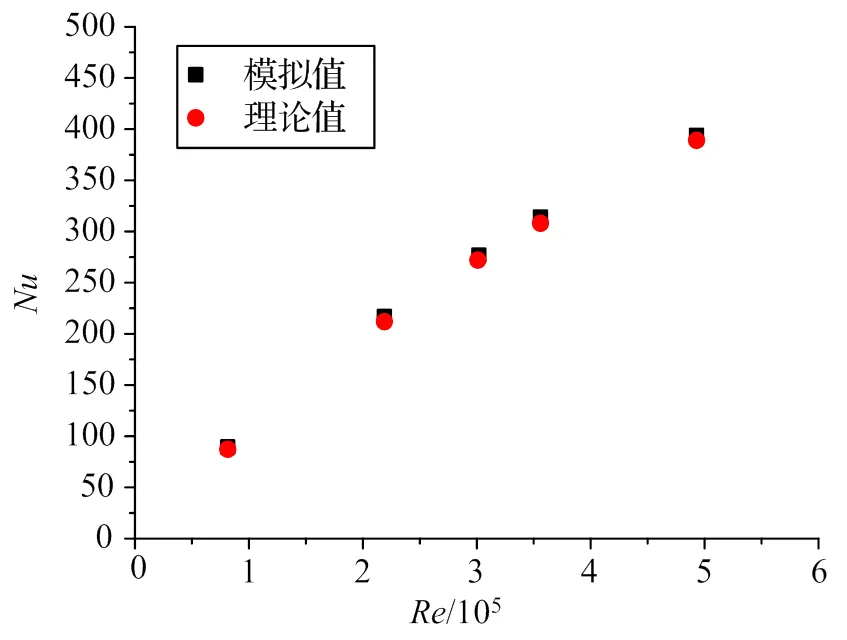
图3 平板处于层流状态时Nu模拟值和理论值对比

对于雷诺数＜500000，平板处于层流状态，理论值根据如下经验公式计算：

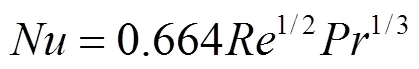
3 高雷诺数算例

选取管道直径为1 m，管长为20 m，取马赫数为0.1、0.2、0.4、0.6的四种工况进行验证，流体温度100 K，管壁温度150 K，流体压强为1 bar。边界条件为进口采用压力进口，出口采用压力出口，壁面采用无滑移恒定壁面温度。

经过计算，管内流动模拟值与理论值对比如图4所示，其中CFD修正模拟值采用式（2）（3）即引入恢复温度进行修正，此时雷诺数范围在107量级。可以看出，模拟值与经验公式计算值整体吻合得较好，尤其在低马赫数时CFD未修正值和修正值差别不大、且均和D-B公式和Gnielinski公式吻合很好，这是由于低马赫数时恢复温度近似等于流体静温。而在高马赫数，可以看出采用恢复温度修正过后的CFD换热系数模拟值与Gnielinski吻合很好，而未修正过的CFD模拟值与经验公式计算值差值较大，说明D-B公式和Gnielinski公式可以应用于低温风洞中的高雷诺数范围进行工程计算，并且在采用CFD数值模拟进行求解换热系数时在高马赫数时需要用恢复温度对换热系数定义式进行修正。

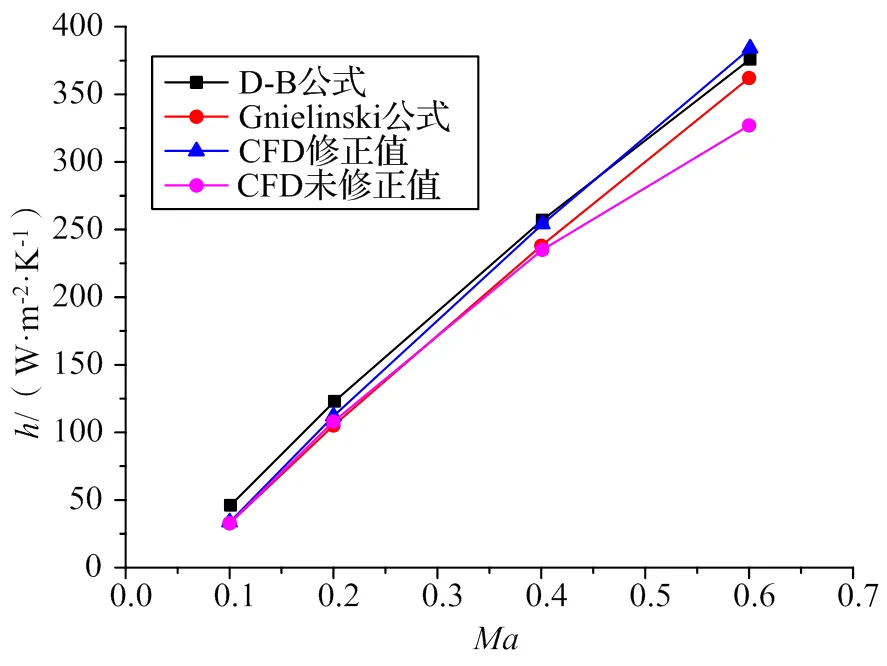
图4 换热系数CFD模拟值与经验公式值对比

4 超音速等直径管换热

对超音速流速下的等直径圆形管道进行CFD数值模拟，用Fluent求解超音速换热时采用密度基瞬态求解，直到算到稳态，考虑气体的可压缩性，流体物性采用Refprop软件拟合。考虑长径比为10的等直径管及长径比为2的等直径管，如表1所示。边界条件为进口采用压力进口，出口采用压力出口，壁面采用无滑移恒定壁面温度。

表1 等直径管参数及其流体工况参数

4.1 算例1结果分析

由图5可以看出，在0.3 m附近，即管长为直径的3倍长度时，马赫数有一个从超音速向亚音速的突变，出现管道堵塞现象[12]。即实际气体在等直径管中流动，等直径管道相当于渐缩管，考虑摩擦作用时由超音速气流不能连续转变为亚音速气流，出口的极限状态只能为声速。

图5 算例1的马赫数分布

4.2 算例2结果分析

由图6可以看出，管内超声速的流动现象基本上是符合理论基础的，即等直径管内超声速流动速度减小，但最小减小到跨音速，否则会出现堵塞现象[12]。整个管内的流动均在超音速范围内，说明管长小于限制管长。

图6 算例2的马赫数分布

算例2中，取＝1 bar、＝100 K、＝1.21×108，通过式（2）（3）采用恢复温度对处于超音速工况流体求解换热系数的定义式进行修正求得(CFD)＝986 W/(m2·K)，通过式（4）和（8）求得(D-B)＝928 W/(m2·K)，通过式（8）～（10）求得(Gnielinski)＝940 W/(m2·K)。可以看出D-B经验公式和Gnielinski公式与CFD修正后的仿真结果均吻合较好，且两个公式计算结果在雷诺数在108这个量级的计算结果相差不大，可以说明D-B公式和Gnielinski公式在超音速高雷诺数的适用性。

5 收缩喷管段实际模型换热分析

为进一步验证D-B公式和Gnielinski公式在超音速高雷诺数下的适用性，对低温风洞收缩喷管段实际模型针对静温变化比较大的工况进行CFD模拟。如图7所示的风洞收缩喷管段结构模型，分为收缩段、硬板喷管段、柔板喷管段三个部分。

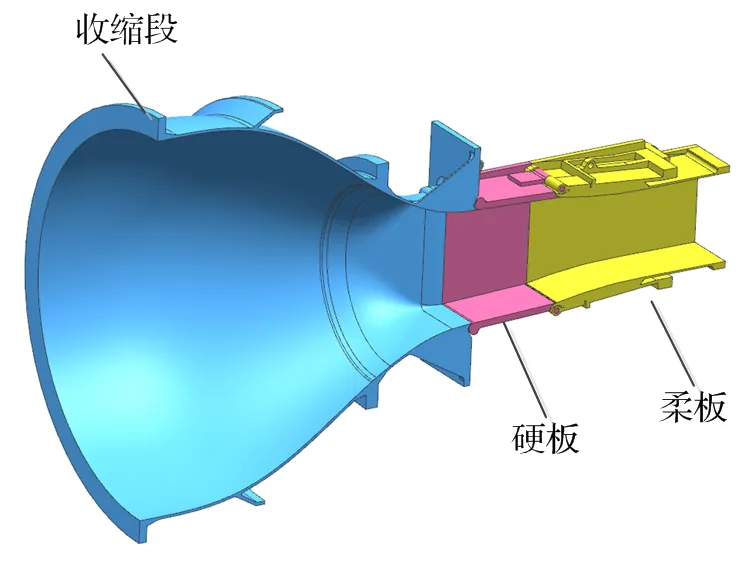
图7 风洞收缩喷管段模型

氮气实现跨音速流动，需要考虑工质压缩性，使用压力边界条件，进口压力为inlet,total＝3.5 bar，出口压力为outlet,static＝1.263199 bar，出口马赫数达到1.3。壁面边界条件对于静态流场分析，壁面采用恒壁温边界条件，壁面是气动降温过程，流体壁面温度设置为比流体入口主流温度高50 K。

计算结果如图8所示，压力沿流动方向逐渐减小，速度逐渐增大，在喉部位置氮气流速达到音速，v＝194.05 m/s。喷管内氮气压力不断降低，流速不断增加，内腔体壁面换热性能沿气流方向不断变化。

由图9所示的换热系数分布可以看出，缩放喷管换热系数沿流动方向先增大后减小，顶部柔板的峰值在喷管喉部之前＝312 mm时最大值为1351.56 W/(m2·K)，侧壁面的峰值也分布在喉部之前的位置，＝410 mm时最大值为1115.33 W/(m2·K)，有文献[4]中研究发现CFD模拟值在喉部以前略小于实验数据，在喉部以后与实验数据吻合较好，且热流密度的峰值在喉部以前。比较图9（a）（b），可以看出本文模拟的喷管段换热系数变化规律与文献中的趋势完全一致，且峰值的位置也一致，说明了模拟的正确性。

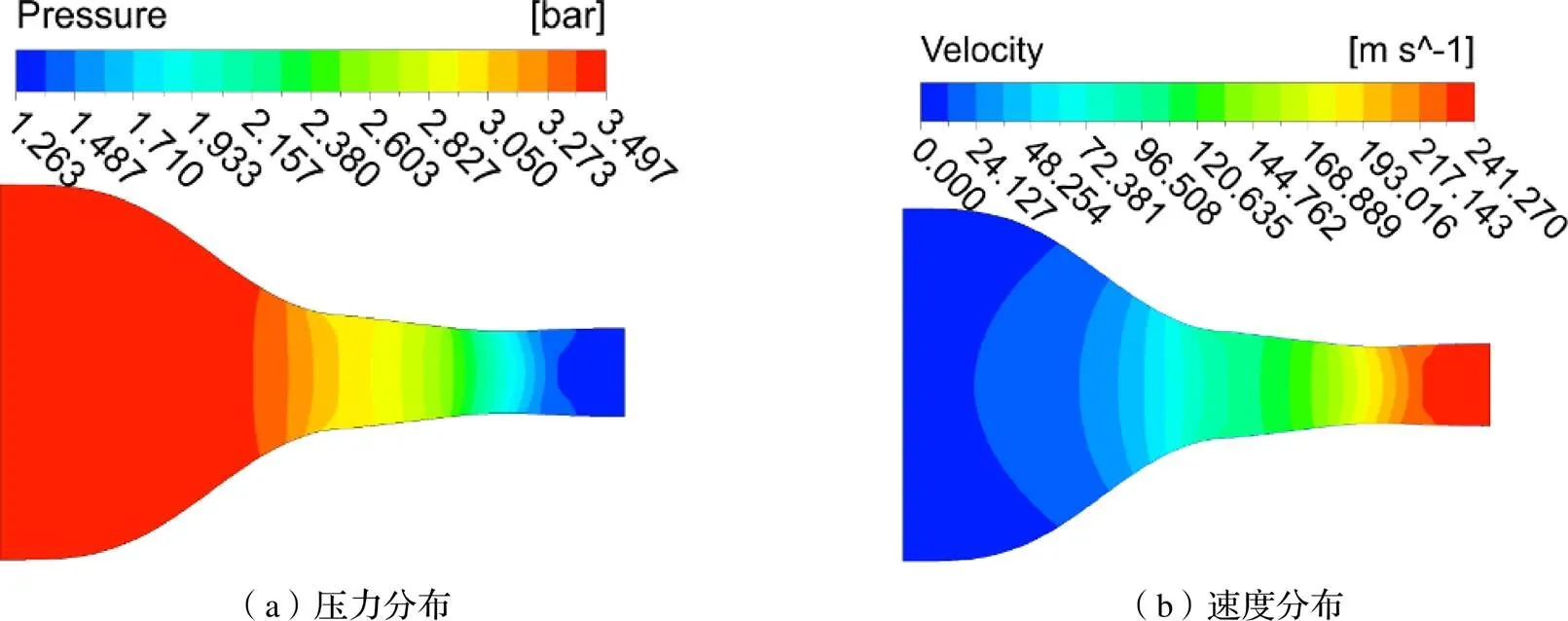
图8 喷管流场仿真结果云图

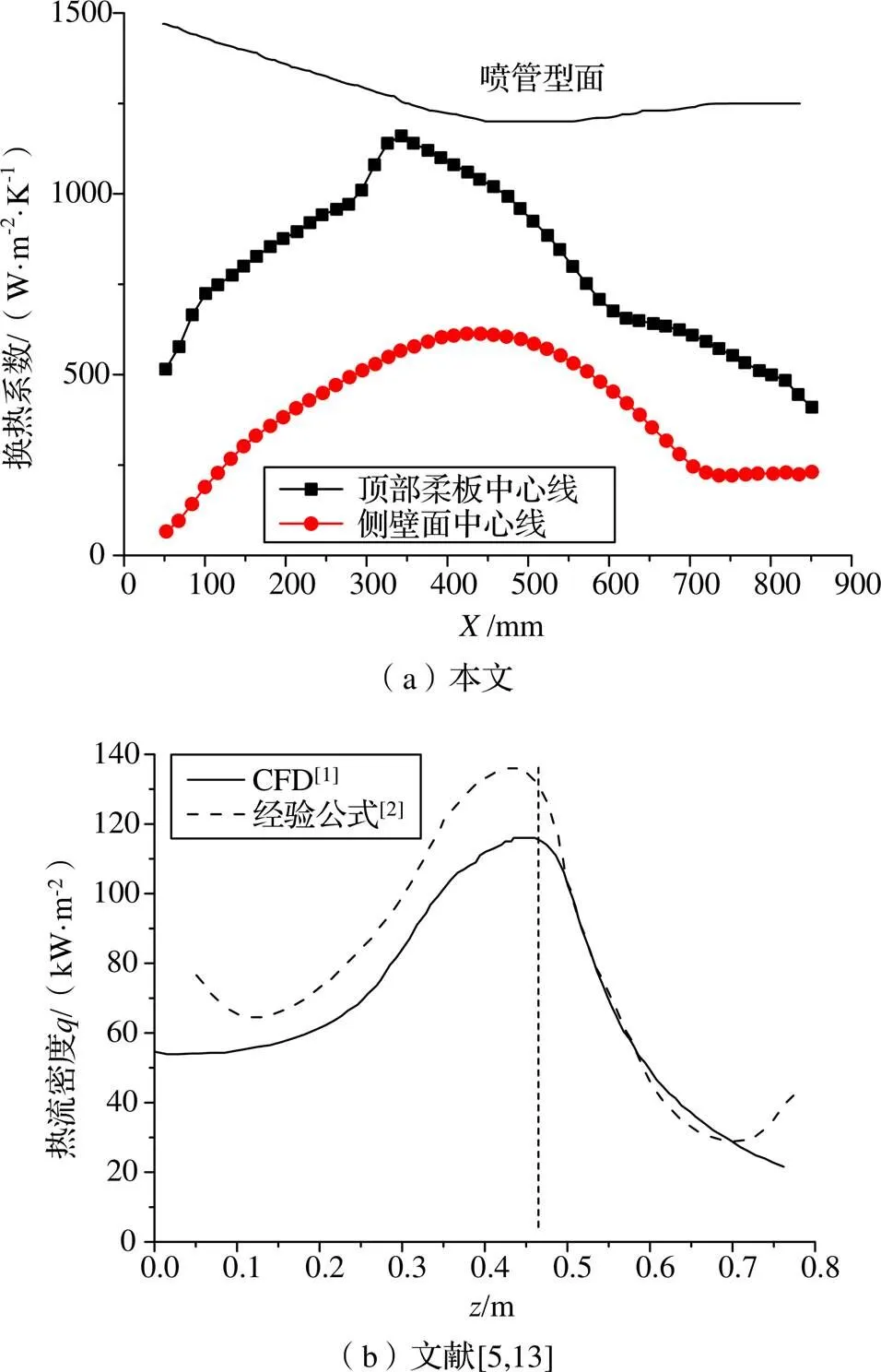
图9 沿喷管型线换热系数分布

使用经验公式对喷管柔板处换热系数进行工程计算，柔板段模型为缩放喷管，取平均当量直径为d＝4A/＝0.2928 m。缩放喷管气流速度始终增大，取当地音速v＝194.05 m/s作为平均速度，根据压力分布云图取柔板处压力为1.988 bar，温度取静温static＝94.184 K，计算物性根据工况条件通过NIST进行查找，计算结果如表2所示。

表2 流体物性参数

在＝194.05 m/s条件下求取喷管柔板处流道的面平均换热系数，将数值分析值与经验公式计算值进行对比，分析两者误差，验证数值分析的准确性。对比结果如表3所示，考虑到速度、温度、压力均为变化数值，取平均值会引起误差，则计算结果可靠。

表3 喷管柔板换热系数对比结果

6 总结

通过对低温流体超音速及其高雷诺数的换热特性通过CFD和经验公式对比分析，得出了在超音速及其高雷诺数工况，使用恢复温度修正后的Dittus-Boelter公式和Gnielinski公式在高雷诺数时仍然具有实用性，并且两个公式在雷诺数在108这个量级误差很小，在106～108量级，Dittus-Boelter公式的计算结果偏大。

此外，本文对低温风洞收缩喷管段实际模型进行了CFD仿真，与经验公式的算例结果进行了对比分析，验证了采用恢复温度修正传热换热系数定义公式进行CFD数值模拟计算换热系数的科学性，以及两个公式在高雷诺数范围的工程适用性。

[1]Goodyer M J，Kilgore R A. High-Reynolds-Number Cryogenic Wind Tunnel[J]. Journal of the Japan Society for Aeronautical & Space Sciences，2013，42（480）：26-31.

[2]赖欢，陈振华，高荣，等. 大型高速低温风洞冷量回收的方法研究[J]. 西安交通大学学报，2016，50（6）：136-142.

[3]刘政崇. 风洞结构设计（精）[M]. 北京：宇航出版社，2005.

[4]麻越垠，陈万华，王元兴，等. 基于ABAQUS的低温风洞扩散段结构-热耦合仿真研究[C].中国计算力学大会2014暨钱令希计算力学奖颁奖大会，2014.

[5]严慧芳，曾军，娄德仓，等. 高速喷管内部对流换热计算方法研究[J]. 航空科学技术，2015（10）：68-72.

[6]毛旭. 对流换热边界下高超音速平板边界层相似性解研究[D]. 天津：天津大学，2013.

[7]Back L H，Massier P F，Gier H L. Convective heat transfer in a convergent-divergent nozzle[J]. International Journal of Heat and Mass Transfer，1964，7（5）：549-568.

[9]杨世铭，陶文铨. 传热学（BZ）（TB）[M]. 4版. 北京：高等教育出版社，2010.

[10]许鹏博，孙晓玲，章锦威，等. 高超声速气动加热/结构传热耦合计算研究[C]. 全国计算流体力学会议，2014.

[11]李鹏飞，吴颂平. 类航天飞机前身结构与高超声速流场的耦合传热模拟分析[J]. 航空动力学报，2010，25（8）：1705-1710.

[12]杜广生. 工程流体力学[M]. 北京：中国电力出版社，2005.

[13]Stoll J，Straub J. Film cooling and heat transfer in nozzles[J]. Journal of turbo machinery，1988，110（1）：57-65.

[14]吴加俊，戴恒震. 基于ABAQUS的导电滑环的单丝静态接触力学特性分析[J]. 机械，2018，7（18）：18-22.

[15]文华，王玲，殷国富，等. 插装阀集成块内部流道流场分析研究[J]. 机械，2017，5（10）：10-13.

Numerical Study of Heat Transfer Characteristics in Cryogenic Wind Tunnel at High Reynolds Number

GAO Xinyu，NIE Xutao，CAI Qingqing，ZHANG Wei

(China Aerodynamics Research and Development Center, Mianyang 621000, China )

The heat transfer characteristics of cryogenic wind tunnel under supersonic and high Reynolds number conditions are the key factors to analyze the distribution of the temperature field in cryogenicwind tunnel. The heat transfer characteristics under supersonic and high Reynolds number conditions are simulated by using the recovery temperature correction heat transfer coefficient calculation method, and the results are compared with the calculations by Dittus-Boelter equation and Gnielinski equation. The results show that the application of D-B formula and Gnielinski equation under supersonic and high Reynolds number conditions after the recovery temperature correction still have a high validity. Finally, the numerical simulation results of the spray pipe section are compared with the predicated values and analyzed, which further verifies the applicability of the average heat transfer coefficient obtained by the above two equations and the validity of the recovery temperature correction heat transfer coefficient calculation formula with non-uniform temperature distribution.

cryogenic wind tunnel；high Reynolds number；supersonic；heat transfer characteristics；recovery temperature

TB69

A

10.3969/j.issn.1006-0316.2021.11.005

1006－0316 (2021) 11－0034－07

2021－01－22

高鑫宇（1985－），男，四川仁寿人，硕士，工程师，主要研究方向为风洞设备结构设计等，E-mail：gaokerry@126.com；聂旭涛（1979－），男，安徽宿松人，博士，副研究员，主要研究方向为风洞设备结构设计等。