基于改进TOPSIS法的城市空气质量综合评价

郭三党， 李 倩， 荆亚倩

（河南农业大学信息与管理科学学院，郑州 450002）

随着城市化水平的不断提高，资源和能源的大量消耗以及车辆保有量的快速增加，大量有毒有害气体如可吸入颗粒物（PM10）、二氧化硫（SO2）和二氧化氮（NO2）等被释放到空气中，造成温室效应、酸雨和其他环境问题，导致环境空气质量显著下降. 改善空气质量是解决环境问题的有效途径，实现这一改善的最重要步骤之一是检测空气质量水平.

评估空气质量除了单污染物因素（SO2、NO2、PM10）分析法［1-3］，还有许多综合方法，如模糊综合评价法［4］、空间自相关法［5］、灰色聚类评价法［6］、多属性决策分析［7］、决策树［8］、神经网络［9］和层次分析法［10］. 易睿和丁志成［11］采用层次分析法（AHP），利用SO2、NO2和PM10作为评价因子，对扬州市2005—2010 年的空气质量进行评价，但污染物因子不完全的空气质量评价不具有普遍性；Monforte和Ragusa［12］使用空气质量指数（AQI）评估了2013—2015年地中海地区的空气质量，虽然AQI可以简单直观地反映空气质量水平，但没有考虑多种污染物之间的相关性；李成和李坤权［13］利用双权重因子模糊综合评价方法评价南京市2013—2016年空气质量，但模糊综合评价方法决策受主观因素的影响，不能提供客观准确的评价；杨瑞君等［14］提出基于随机森林模型的评价方法，对上海市空气质量进行了评价.

以上关于空气质量评价的文献中，专注于单一污染物对空气质量的影响和仅检测空气质量指数两方面的研究，不符合公众接触多种污染物的实际情况，并且AQI并不能反映污染物之间的关系. 因此，构建多污染物加权空气质量综合评价模型有意义也有必要. 本文依据《环境空气质量标准》（GB 3095—2012）［15］，选取PM2.5、PM10、SO2、CO、NO2和O3作为主要空气污染物，以此建立了污染物因子评价指标集，在此基础上采用相对熵理论得到指标综合权重，建立了改进TOPSIS法的评价模型，用绝对理想解代替相对理想解，通过马氏距离计算各评价样本的相对贴近度，解决了指标逆序和相容性问题. 最后，将改进TOPSIS法的评价模型应用于郑州市2020年11月的空气质量评价，并与改进前的TOPSIS法和AQI法进行对比分析，验证了评价结果的合理性和可行性.

1 问题描述与模型构建

1.1 问题描述

假设有m个评价样本，n个评价指标，原始评价矩阵为X=(xij)m×n(i=1,2,…,m；j=1,2,…,n)，其中xij为第i个样本第j个指标的原始评价值：

采用极值法对原始评价矩阵X=(xij)m×n进行标准化处理，得到标准化矩阵C=(cij)m×n：

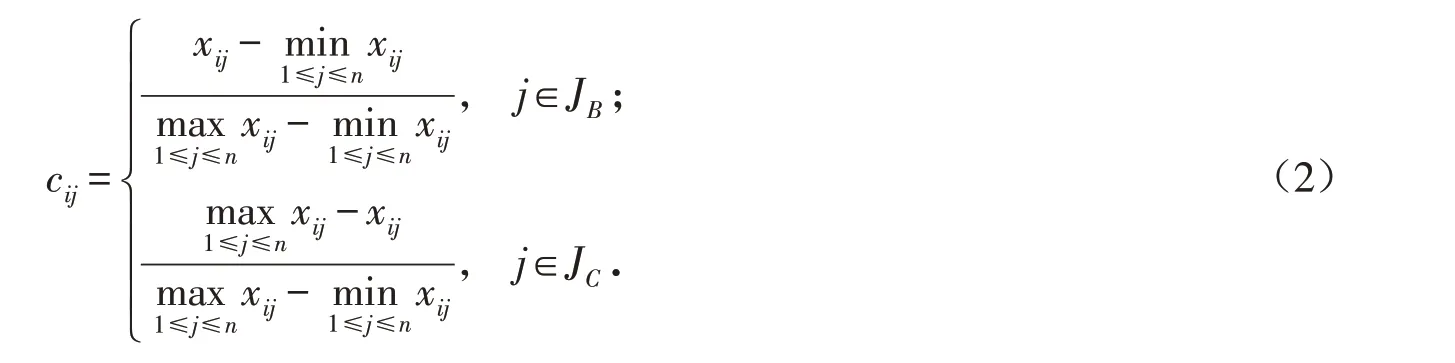
式中：JB属于效益型指标；JC属于成本型指标.

1.2 指标权重确定

各污染物权重的设置对于评价结果至关重要，目前确定指标权重的方法主要有主观赋权法和客观赋权法. 主观赋权法根据专家自身经验合理地确定各指标权重，但决策结果具有较强的主观随意性. 客观赋权法通常是基于比较完善的数学理论依据，根据指标原始评估值之间的关系来确定各指标权重，客观性强，但是客观赋权法不能体现决策者对各指标的重视程度. 因此指标的赋权要综合考虑主客观权重，既兼顾决策者对指标的偏好，同时要减少主观性. 本文利用熵权法确定指标客观权重，根据专家经验确定指标主观权重，通过相对熵理论将主客观权重相结合得到指标综合权重.

1.2.1 指标客观权重的确定 熵权法最早由Shannon和Weaver提出，是一种客观赋权法，其本质是通过数据值的变异系数来确定指标的权重［16］. 熵权法计算的步骤如下［17］.

1）对数据进行归一化，得到归一化矩阵P=(pij)m×n.

式中：

2）计算第j个指标的熵值：

式中：第j个指标的变异性越大，ej越小；变异性越小，则ej越大；若ej=1，说明第j个指标对评价体系没有影响.

3）计算第j个指标熵的变异系数：

4）确定基于熵的指标权重δ=(δ1,δ2,…,δn)：

1.2.2 指标主观权重的确定 主观赋权法根据决策者主观上对各指标的重视程度对权重做出判断［18］，设η=(η1,η2,…,ηn)为指标主观权重，满足各指标权重之和等于1，如公式（7）所示：

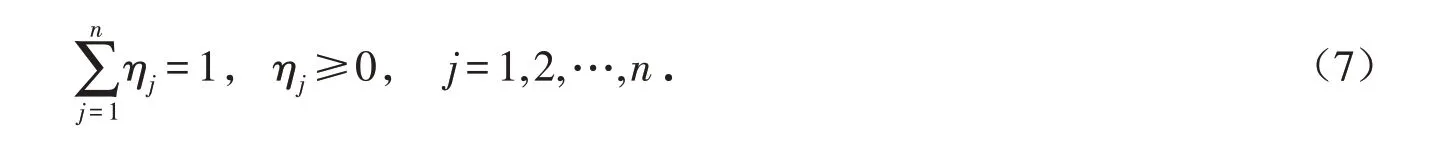
1.2.3 指标综合权重的确定 设δ=(δ1,δ2,…,δn)为熵权法求出的指标客观权重，η=(η1,η2,…,ηn)为指标主观权重，根据最小相对熵原理［19］，对指标综合赋权，设评价指标综合权重为ω=(ω1,ω2,…,ωn)，则综合权重通过下面的目标函数求出：

由此可以求得各指标的综合权重ω=(ω1,ω2,…,ωn)的计算公式为：

1.3 改进TOPSIS法综合评价模型

1.3.1 传统TOPSIS模型 TOPSIS评价方法对样本、指标无特殊要求，使用灵活简便. 基本步骤如下［20］：

1）计算加权标准化决策矩阵Z=(zij)m×n：

式中：cij为第i个样本第j个指标的标准化评价值；ωj为各指标综合权重.

2）确定各评价指标的正理想解Z+和负理想解Z-：

4）计算各样本基于正理想解和负理想解的相对贴近度ci：

5）根据ci值对各样本排序，ci越小空气质量越好，样本越优.

1.3.2 改进TOPSIS 法构建步骤 虽然传统的TOPSIS 法有很多优点，但在应用时也存在一定的局限性. 如逆序问题，即在评价过程中当增加（或删除）几个评价对象时，会产生评价结果顺序的变化；由于指标之间存在隐含的关联性，即指标相容性问题，而TOPSIS法一般采用欧氏距离计算相似度，欧氏距离是空间中两点之间的线性距离，未考虑指标之间的相关性. 因此，用欧氏距离计算的TOPSIS法评价值并不能真正反映每个样本的优势. 本文针对上述问题进行了改进，用绝对理想解代替相对理想解消除逆序问题，无论增加还是减少方案，都不会出现逆序问题［21］. 用马氏距离代替欧氏距离来解决相容性问题，与欧氏距离相比，马氏距离能更好地反映指标之间的相关性［22］. 改进TOPSIS法的步骤如下：

式中：Xi={xi1,xi2,…,xim}；ε为关联系数矩阵；Λ=diag(ω1,ω2,…,ωn)，ωj是第j个指标的综合权重.

采用邓氏关联度，指标间关联系数计算公式如下：

式中：ρ是分辨率，在这里取ρ=0.5.

则关联系数矩阵ε为：

3）计算各样本基于绝对正理想解和绝对负理想解的相对贴近度：

改进TOPSIS评价方法的流程图如图1所示.

图1 改进TOPSIS法建模流程Fig.1 Flow chart of improved TOPSIS method modeling

2 实例分析

2.1 数据来源

以中国环境监测总站发布的《全国城市空气质量报告》数据（http：//www.cnemc.cn/）为依据，参考《环境空气质量标准》（GB 3095—2012）［15］，选取郑州市2020 年11 月6 种空气污染物（PM2.5、PM10、SO2、NO2、CO 和O3）的日均浓度检测值（表1）. 根据以上建立的改进TOPSIS模型，将各评价指标的数据代入评价系统中，对郑州市2020年11月的空气质量进行综合评价.

表1 郑州市2020年11月6种空气污染物日均浓度值Tab.1 The daily average concentration values of six air pollutants in Zhengzhou City in November 2020单位：μg/m3

2.2 数值计算

利用公式（6）计算6种污染物基于熵权法的客观权重：

结合郑州市实际空气质量状况及专家意见，给出6种污染物主观权重：

利用公式（9）计算6种污染物指标综合权重：

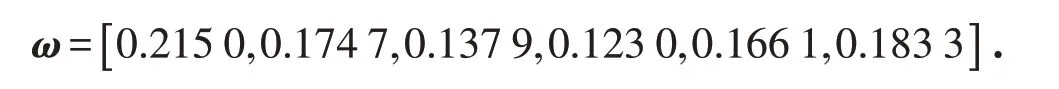
根据公式（14）确定绝对正（负）理想解：

利用公式（16）计算6种污染物指标之间的关联系数（表2）.

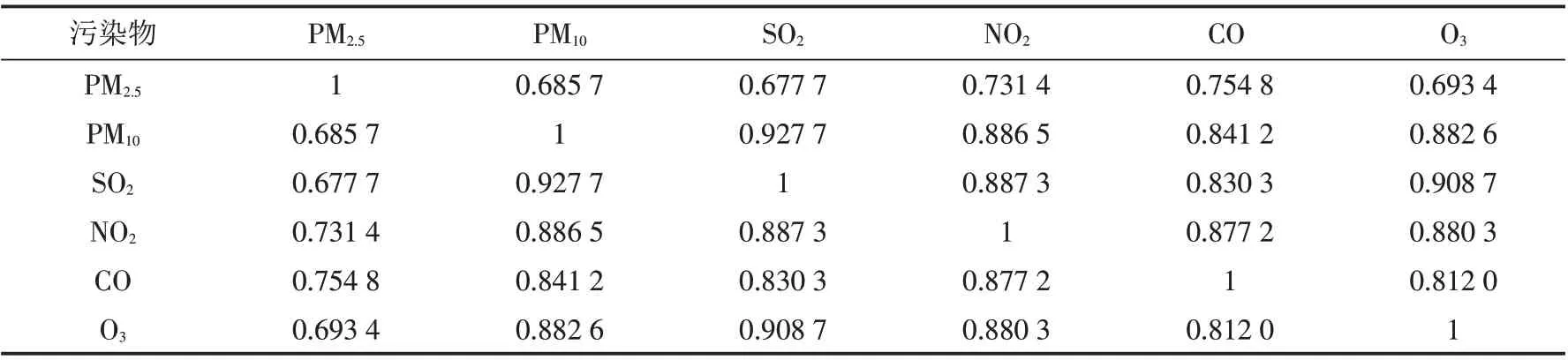
表2 6种污染物指标之间的关联系数Tab.2 Correlation coefficients among six pollutant indicators

根据公式（15）计算每个样本与绝对正负理想解之间的马氏距离.

为了更明确地表达空气质量状况，参考《环境空气质量标准》（GB 3095—2012）［15］与《环境空气质量指数（AQI）技术规定（试行）》（HJ 633—2012）［23］的规定，对照空气质量等级划分标准得到各个评价样本空气质量等级. 通过对各样本相对贴近度0～1之间的取值进行等级划分，将空气质量划分为6个等级状态，即一、二、三、四、五、六级，分别代表空气质量状况中的优、良、轻度污染、中度污染、重度污染、严重污染（表3）.

表3 空气质量状况等级划分Tab.3 Classification of air quality status

根据公式（18）求得各评价样本与绝对正理想解和绝对负理想解的相对贴近度，将郑州市2020年11月的空气质量状况进行等级划分，结果如表4.

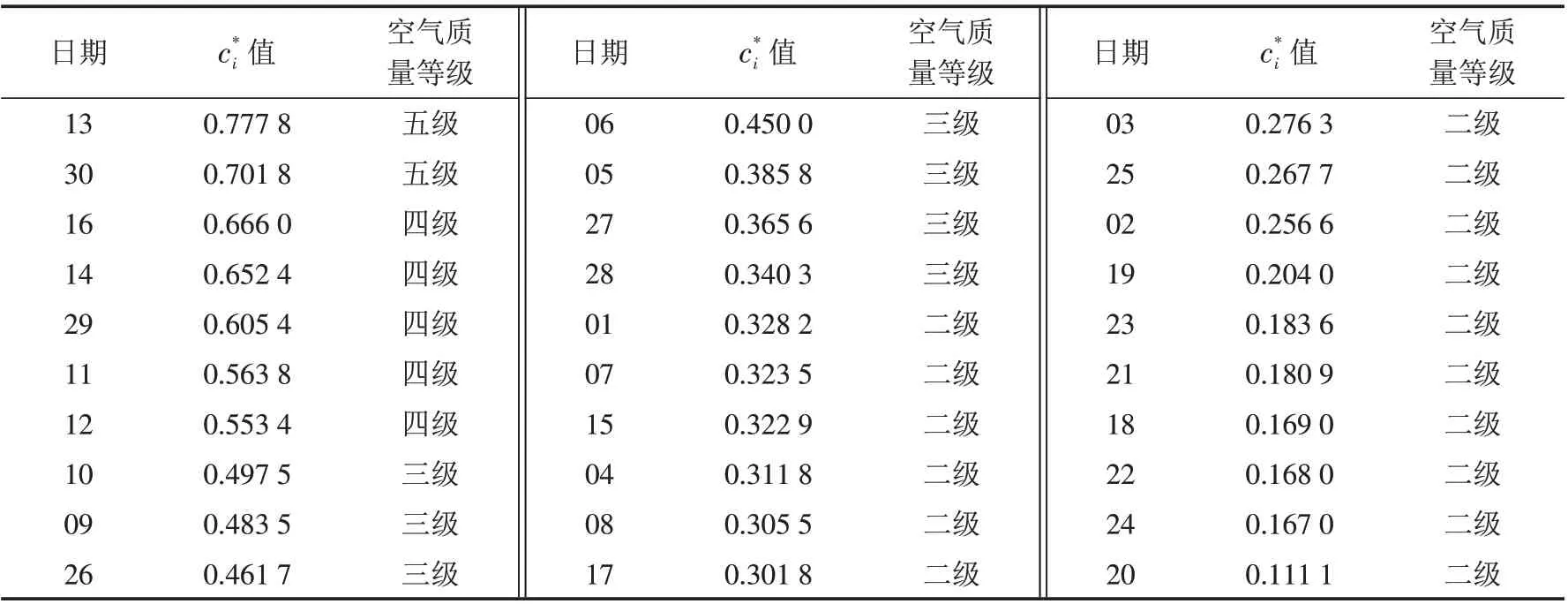
表4 郑州市2020年11月空气质量评估结果Tab.4 Air quality evaluation results of Zhengzhou City in November 2020

2.3 结果分析

根据各指标综合权重值可知，PM2.5的综合权重值（0.215 0）高于其他5种污染物，说明2020年11月PM2.5对郑州市空气质量影响最大，其次是O3、PM10、NO2、SO2和CO，这对如何改善空气质量而言是一个重要的参考信息. 从表2可以看出，一些指标之间有很高的关联性，比如PM10和SO2的关联系数达到0.927 7，O3和SO2的关联系数为0.908 7，说明PM10和O3对SO2影响显著. 此外，一些指标间关联性较低，如PM2.5和SO2关联系数只有0.677 7，说明PM2.5与SO2之间关系相对较弱. 因此改进TOPSIS法与TOPSIS法相比，有着可以反映指标间相关性的优势.

为了验证改进TOPSIS法的准确性和可靠性，采用该算法与TOPSIS法的结果进行比较，并与AQI法进行对比分析，结果如图2和图3（郑州市2020年11月的AQI值可在《全国城市空气质量报告》中查询）. 从改进TOPSIS法和TOPSIS法的评价结果可以看出两种方法的趋势大致相同，但通过TOPSIS法计算出的相对贴近度普遍偏大，这是因为在使用欧式距离计算相对贴近度的评价过程中存在的相容性问题. 改进TOPSIS法克服了这一缺陷，使评价结果更加科学可靠.

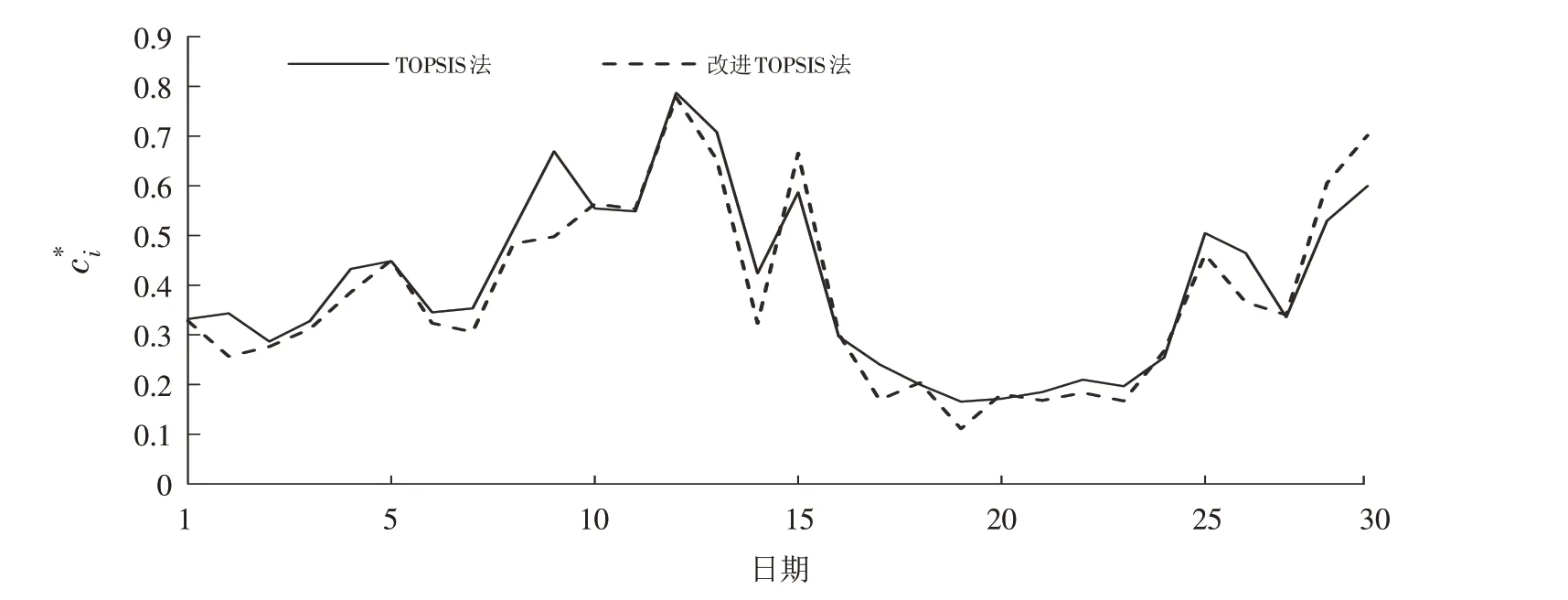
图2 改进TOPSIS法和TOPSIS法对郑州市2020年11月空气质量的评价结果Fig.2 Evaluation results of air quality of Zhengzhou in November 2020 by improved TOPSIS method and TOPSIS method

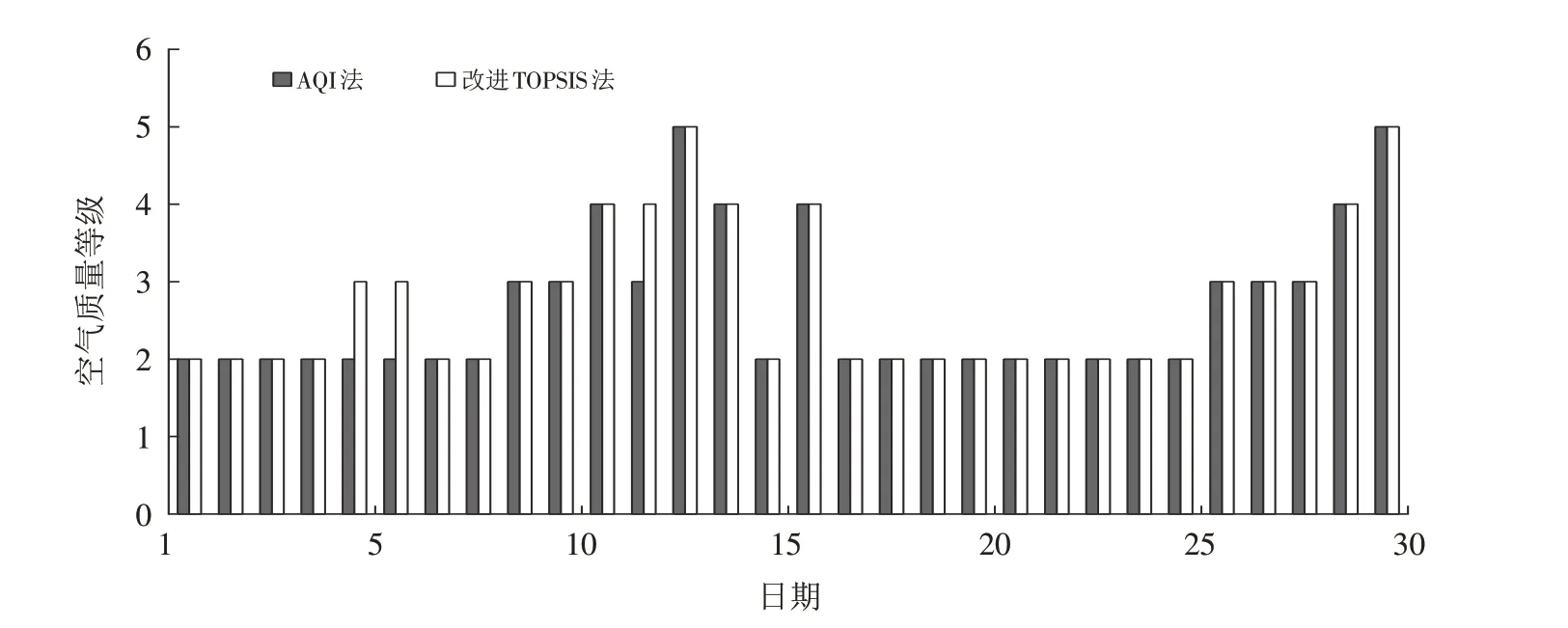
图3 改进TOPSIS法与AQI法对比结果Fig.3 Comparison results between improved TOPSIS method and AQI method

根据改进TOPSIS法与AQI法对比结果（图3）可知，改进TOPSIS法和AQI法对郑州市空气质量的评判结果基本相符，均能反映空气质量状况，证明了本文所提出的改进TOPSIS法的可行性. 但是两种方法评价的侧重点不同，AQI是描述空气质量综合状况的无量纲指数，广泛应用于区域城市空气质量的评价，在技术标准中仅明确了各时点的AQI计算方法，并未明确规定多时点的AQI计算方法，缺乏整体评价概念［24］. AQI可以反映空气污染程度，但不能反映污染物之间的关系，也不能判断影响空气质量的主次因素. 相对于AQI法，改进TOPSIS法通过相对熵理论对各评价指标综合赋权，明确体现了各污染物的重要程度差异，全面考虑所有评价指标对空气质量的影响及其彼此间的关联性，评价精度更高.

3 结论

选取PM2.5、PM10、SO2、NO2、CO和O3作为评价指标，运用改进TOPSIS法对郑州市2020年11月的空气质量进行了全面综合评价. 该方法以相对熵理论综合指标主客观权重，以体现各污染物重要程度的差异，并分析了各污染物之间关联系数的分布特点，通过马氏距离计算相对贴近度，减少了评价过程中的信息损失. 主要结论如下：

1）改进TOPSIS法通过综合赋权确定指标权重，得出PM2.5对郑州市空气质量影响最大.

2）通过分析可知，郑州市2020年11月空气质量总体较好.

3）郑州市2020年11月的空气质量评价实例结果表明，改进TOPSIS法相比TOPSIS法和AQI法更具有良好的评价能力，评价结果更科学可靠.

综上所述，改进TOPSIS评价法具有理论和实践意义，为城市空气质量综合评价提供了一种新的思路.