剪得断，理不乱——制作正方体展开图有感

文／南京师范大学第二附属初级中学 张子岩

学习了“走进图形世界”，我发现正方体的11种展开图中（图略），每幅图都要剪7刀。这是巧合吗？下面，我以其中的一幅图为例，将我的思考过程和大家分享。

思考1：如何说明正方体被剪了几刀？

我尝试将展开图复原成正方体，发现被剪开的棱较多，难以一一标注，没有被剪开的棱较少，于是我将没有被剪开的棱标注成红色（如图1）。

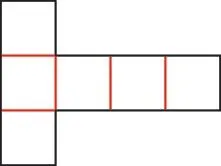
图1

我们都知道，正方体有11 种平面展开图。通过标注，我发现每种展开图中没被剪开的棱都是5条，而正方体有12条棱，所以展开时，需要剪开7条棱，即要剪7刀。

思考2：为什么未被剪开的棱都是5 条？是巧合吗？

“逆向”思考：利用正方形磁力片，我模拟了正方形连接成平面展开图的过程。如图2，将2 块磁力片相连，产生了1 条“未剪棱”。再放第三块磁力片，不管放在哪个位置连接，都会多出1 条“未剪棱”。依次进行下去，我发现，每多放1 块磁力片，就会多出1 条“未剪棱”。正方体共6 个面，即共需要6 块磁力片，因此，连接时一定会产生5条“未剪棱”。

图2

思考3：放1 块磁力片能产生2 条“未剪棱”吗？

我尝试后发现，要想放1块磁力片产生2条未剪棱，首先需要将已经连接的磁力片形成如图3 所示的直角，然后将下一块磁力片放置于右上角的缺口处。但此时会形成“田”字格形状，显然无法折叠成正方体。

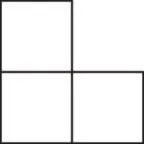
图3

感悟：7 刀剪开正方体，不是巧合，而且未被剪开的棱一定是5条。

延展：我又将三棱锥展开成平面图，发现共需要剪开3条棱。大家可以自己尝试一下。

教师点评

小作者善于从观察、实践中发现规律。更可贵的是，小作者不满足于此，进一步探寻规律背后的原理，力求“知其然，知其所以然”。在研究过程中，“剪”难研究，小作者便研究“未剪”；“断开”难研究，小作者便研究“连接”。这种逆向思维体现了小作者优秀的数学思维品质。