长槽钢轴压构件缀板加劲效应的理论计算方法

李菁文， 沈才华， 汪基伟

(河海大学 土木与交通学院，江苏 南京 210098)

在基础工程中，钢桩插打一直是施工的重难点。事实上，钢桩可看作一较长的轴心受压钢构件，而单轴对称的开口槽钢构件受到轴向荷载作用时，易发生弯曲屈曲现象。近年来研究主要针对槽钢受压构件的畸变屈曲问题，有学者通过改变截面型式来提高构件的稳定荷载，如陈明[1-2]提出腹板加强型槽钢截面，宋波[3]和王春刚[4-7]则分别通过帽型和V型对截面进行局部加劲处理，均采用有限元和试验方法对新型截面构件的稳定性因素深入研究；也有学者通过一些构造措施来提高构件的稳定性能，如顾建飞[8]提出沿构件长度方向布置连杆的措施以防止畸变屈曲的发生，李元齐[9]则是通过在卷边间设置缀板来控制构件畸变屈曲，随后胡启平等[10-12]也采用此措施对构件其他屈曲模式及构件长细比等稳定因素进行研究。总体上，目前采用有限元和试验方法研究槽钢构件畸变屈曲的局部加劲的成果较多，少有对构件弯曲屈曲进行加劲处理的理论研究。

理论方法既便于理解也便于应用，本文针对槽钢轴压构件的弯曲失稳模式，基于《钢结构设计规范》(GB 50017—2013)稳定临界荷载的计算思路，提出一种沿构件长度方向(称为纵向)布置缀板以防止其发生弯曲屈曲的构造措施，并给出带缀板的槽钢轴压构件的稳定荷载理论计算方法。

1 基于空间配位法思想的长槽钢缀板加劲理论计算公式推导

目前现行钢结构规范中对设置缀板的长槽钢柱加劲缺乏理论计算，本文考虑缀板的尺寸效应和其加劲位置影响，对此提出空间配位法思想，建立了缀板加劲构件的稳定荷载的理论计算方法。具体计算方法的思路如下：

首先采用规范中稳定计算方法分别计算未加劲的原槽钢构件(图1)，对纵向布置同构件等长度的一整块缀板下的槽钢构件(称为全加劲的槽钢构件，如图2，图中蓝色实线为缀板)的临界荷载值，然后将有间距布置缀板相对于全加劲构件的刚度的折减作用简化为线性函数，最后考虑缀板的空间位置效应，构造位置函数，引入换算系数，从而有效且快速得到换算后的临界荷载值，即带缀板的槽钢轴压构件的稳定临界荷载值。

图1 原槽钢构件横截面示意图Fig.1 Schematic diagram of cross section of original channel steel member

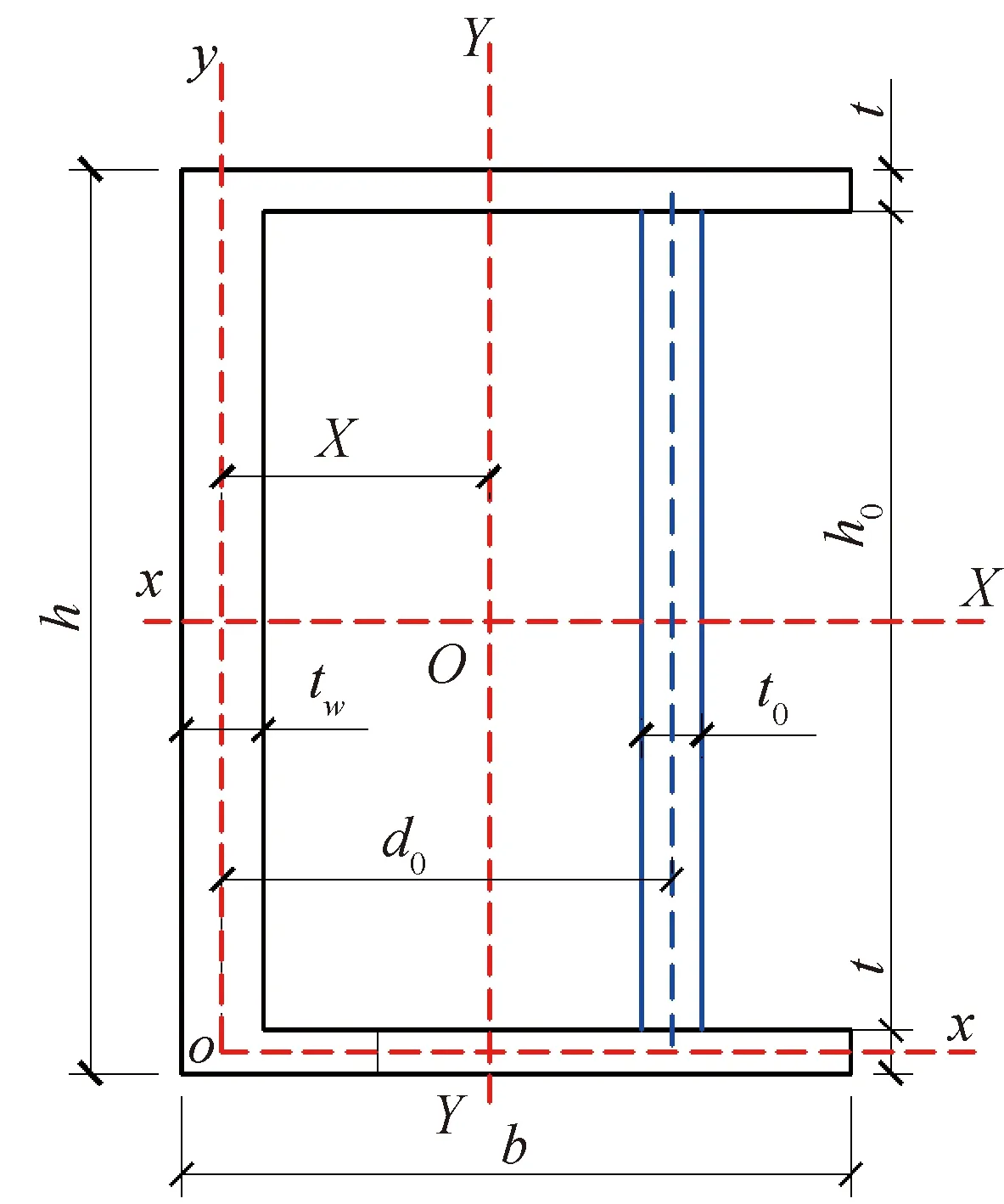
图2 全加劲槽钢构件横截面示意图Fig.2 Schematic diagram of cross section of fully stiffened channel steel member

1.1 原槽钢构件和全加劲构件整体稳定计算

1.1.1 原槽钢构件

图1中，XOY为原槽钢构件形心坐标系，xoy为相对坐标系。根据GB 50017—2013规范中整体稳定的计算方法，原构件的稳定临界荷载N1max按下式计算：

N1max=φ1·A1·f

(1)

A1=2bt+tw(h-2t)

(2)

式中：φ1—原构件的稳定系数，根据构件的长细比λ1、截面分类确定；A1—原构件的截面面积，m2；f—钢材的抗压强度设计值，N/mm2；b—翼缘板的宽度，mm；t—翼缘板的厚度，mm；h—构件的截面高度，mm；tw—槽钢腹板的厚度，mm。

1.1.2 全加劲的槽钢构件

采用规范的方法，对截面特性中截面面积A2和截面惯性矩Iy2进行修正，修正公式如下：

A2=2bt+(tw+t0)(h-2t)

(3)

(4)

(5)

式中：x2—全加劲构件截面形心在xoy坐标系的横坐标，mm；t0—缀板的宽度，mm；d0—横截面上缀板轴线处至腹板厚度轴线处的距离，mm。

故全加劲构件的稳定荷载N2max计算公式为：

(6)

(7)

1.2 长槽钢缀板加劲的空间配位法思想与计算过程

钢桩插打时，为确保土体与桩之间充分的咬合力，缀板纵向布置时会保持一定间距而不采用全加劲布置。考虑缀板设置时的位置效应和其自身的尺寸效应，提出空间配位法思想，具体如下：纵向缀板加劲效应一定介于原构件和全加劲之间，因此引入空间配位法的综合换算系数δ，可得加劲构件的稳定临界荷载的计算公式，具体如下：

Nmax=δ(N2max-N1max)+N1max

=(1-δ)·N1max+δ·N2max

(8)

1.2.1 基本假定

图3 缀板纵向加劲示意图Fig.3 Schematic diagram of longitudinal stiffening of plate

(2)每单块缀板的加劲作用范围仅在相邻两块板中心轴线处之间(构件左、右边界亦看作为一块板)，每块缀板的加劲作用叠加之后为总加劲作用。

(3)假定配位权重时采用线性假设，即部分加劲对全加劲构件刚度的换算作用简化为线性函数。

1.2.2 位置函数的定义

位置函数是表示某一缀板在槽钢纵向某一位置时该板对原构件稳定的增强作用的线性函数，其作用是体现缀板的尺寸效应和位置效应。以构件纵向方向为x轴，构件纵向对称轴处为y轴，建立xoy坐标系。

(1)布置一块板时的位置函数

图4 布置一块板的位置函数示意图Fig.4 Diagram of the position function of one plate

(9)

(2)布置n块板时的位置函数

(10)

每块板都对应着一个位置函数yj，对n块板来说就有n个位置函数yj，取较大的yj作为加劲n块板的位置函数y，如图5黄色实线所示，其他图亦同。

图5 布置n块板的位置函数示意图Fig.5 Diagram of the position function of some plate

1.2.3 换算系数δ的求解

结合位置函数，可引入一换算系数δi，其为每一单块板对整个槽钢构件的加劲增强程度的大小，故共有n块板下的换算系数为

(11)

图6 缀板加劲时换算系数计算示意图Fig.6 Schematic diagram of conversion coefficient calculation when stiffening plate

1.2.4 对称布置的三块缀板加劲增强的理论计算分析

应用公式(11)以对称加劲三块缀板为例对换算系数进行公式推导，得到公式(12)、(13)，并以长度l=30 m的构件进行公式的验证与应用，对不同缀板布置距离下的换算系数进行规律性分析，并绘制图7。

图7 对称加劲三块板下位置函数示置图Fig.7 Diagram showing the position function under three symmetrical stiffening plates

(12)

S阴影=S左右阴影+S中阴影

(13)

(16)

式中:JDx—位置函数交点的x轴坐标，mm。

由图8可知，外侧两块的缀板分别远离构件纵向对称轴处时，换算系数呈先增大后减小的规律，故存在一极大值0.104 7，极大值点位于7.125 m处，即外侧两块板布置在槽钢纵向四分之一处，此时加劲布置示意图见图9。

图8 对称加劲三块板时布置距离与换算系数的关系图Fig.8 The diagram of the relation between the arrangement distance and the conversion coefficient when three plates are stiffened symmetrically

图9 对称加劲三块板时换算系数最大所对应的加劲示意图(单位：m)Fig.9 Schematic diagram of the stiffening corresponding to the maximum conversion factor when three plates are stiffened symmetrically

2 缀板加劲效应的影响因素及其影响规律分析

本节采用《热轧型钢》(GBT-706—2008)中40C槽钢(采用Q420钢材)进行缀板设置，探究缀板加劲效应的影响因素，即缀板布置数量、缀板宽度、缀板布置方式和构件长度。缀板布置方式有一块缀板中心布置、两块缀板对称布置、三块缀板对称布置、四块缀板相邻等间距对称布置和五块缀板相邻等间距对称布置这五种工况。将同槽钢翼缘厚度的18 mm缀板布置在槽钢翼缘边缘处，根据公式(1)—(3)可求得构件长度为30 m时在未加劲下的稳定荷载N1max=15.74 kN和在全加劲下N2max=93.16 kN。

2.1 构件等长度时不同缀板数量加劲总面积对稳定荷载值的影响规律

假定构件截面高度h=1 m和构件长度l=30 m，分别计算不同缀板数量下对应的加劲总面积、相同加劲总面积下各缀板布置方式的换算系数及其对应的临界荷载。其中，最小加劲面积为6 m2；最大加劲面积为30 m2，即全加劲，此时换算系数为1。应用公式(8)计算不同加劲面积下的稳定荷载，并绘图10。

由图10可知，加劲一块时对稳定临界荷载的增强效果最好，其次是五块和四块。事实上布置一块板时未考虑到多块板相邻之间加劲增强的叠加效应，且配位权重时采用了线性假设，与实际情况不符，故在实际工程建议采用多块板对称加劲布置；构件等长度时，加劲面积较小时，加劲布置方式对于加劲作用有一定影响，而加劲面积较大时，加劲布置方式的影响不是很大。

图10 构件等长度(30 m)时不同缀板加劲总面积与稳定荷载的关系图Fig.10 The diagram of the relationship between the total area of stiffening of different plates and the stable load when the member is of equal length (30 m)

为深入研究缀板布置方式对于构件稳定性能提升快慢的影响，对稳定荷载进行变化率计算并绘图11。

图11 构件等长度(30 m)时不同缀板加劲总面积与稳定荷载变化率的关系图Fig.11 The diagram of the relationship between the total area of stiffening of different plates and the change rate of stable critical load when the member is of equal length(30 m)

由图11可知，同长度的构件在加劲总面积越来越大时，变化率越来越小，在趋近于30 m2即全加劲时尤为明显；在加劲总面积为22 m2前，设置两块板时的稳定临界荷载的变化率最为显著，随后则是加劲三块时较明显。故若工程需快速提升构件的稳定性能时，可设置两块缀板的构造措施进行稳定性加固。

2.2 缀板等加劲总面积时不同构件长度下对稳定荷载值的影响规律

假定构件截面高度h=1 m，缀板加劲总面积为6 m2(一块6 m×1 m缀板、两块3 m×1 m缀板、三块2 m×1 m缀板、四块1.5 m×1 m缀板、五块1.2 m×1 m缀板)，分别计算在构件长度l=10 m、15 m、20 m、25 m、30 m和35 m下换算系数和稳定荷载，找出最大的稳定临界荷载及其对应的缀板布置位置，并绘图12。

由图12可知，相同加劲面积6 m2下构件越长，构件的稳定荷载越小，缀板加劲效应越不明显；随着构件长度的增大，等间距布置五块板的加劲效果相对其他布置方式也逐步增大；当板与其相邻左右两块板之间等间距时临界荷载值最大。故等间距对称加劲时的增强效果最优。

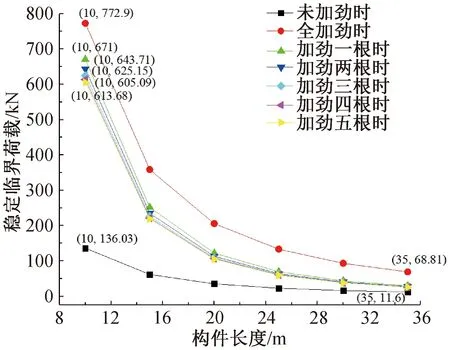
图12 缀板等加劲面积6 m2时不同长度与稳定荷载的关系图Fig.12 The diagram of the relationship between different lengths and the stable load when the stiffening area is 6 m2

同样，为得出缀板布置方式对提升构件稳定荷载快慢的影响，对稳定荷载进行变化率的计算并绘图13。由图13可知，当构件长度不断增大时，稳定荷载的变化率越来越小，同时等间距布置五块板的变化率较大。故对长构件采用等间距对称布置缀板能够使构件的稳定荷载值更快提高。

图13 缀板等加劲面积6 m2时不同长度与稳定荷载变化率的关系图Fig.13 The diagram of the relationship between different lengths and the rate of change of stable load when the stiffening area is 6 m2

3 结论

本文针对工程中钢桩插打的弯曲屈曲问题，建立了一种带缀板槽钢轴压构件的稳定理论计算方法，提出了缀板加劲效应，即在构件翼缘开口处沿长度方向布置缀板的对原构件稳定性能的增强效应，解决了开口轴压长构件在实际工程应用中的失稳问题，为此类构件作局部加劲处理提供了理论依据，得出以下结论：

1)根据缀板的受力特点，提出的空间配位法思想能够有效量化缀板的位置效应和其自身的尺寸效应，可以为稳定设计提供参考。

2)以40C槽钢为例，对缀板的数量、面积(即缀板板宽)、布置方式和构件长度的因素进行构件稳定荷载的规律性分析，计算结果和规律基本合理，验证了基于空间配位法的带缀板槽钢轴压构件的稳定理论计算方法的合理性。但由于配位权重时采用了线性假设，略有粗糙，有待进一步结合试验进行公式修正研究。