直流动态杂散电流在分层介质中的扩散模型

刘 炜 尹乙臣 潘卫国 杨 龙 张 浩

直流动态杂散电流在分层介质中的扩散模型

刘 炜1尹乙臣1潘卫国2杨 龙1张 浩1

（1. 西南交通大学电气工程学院 成都 610031 2. 北京全路通信信号研究设计院集团有限公司 北京 100071）

为了研究直流牵引供电系统杂散电流的干扰范围和影响程度，将回流系统分布式电路等效为集中电路，建立牵引供电系统集中等效电路，采用节点电压法进行系统潮流计算，基于潮流计算结果，建立全线杂散电流随时间动态分布模型；采用叠加原理建立动态杂散电流在层状介质中的扩散模型，利用Prony法进行求解，与CDEGS软件仿真结果进行对比，地电位计算误差在8.66%以内。国内某地铁线路列车采用6B编组，最大速度80km/h，发车间隔2min，混凝土电阻率为0.503W·km，土壤电阻率为38.9W·m，埋地金属结构与地铁线路距离50m时，钢轨过渡电阻值提高至40W·km以上，或钢轨过渡电阻值为5.31W·km时，埋地金属结构与地铁线路的距离增大至0.25km以上，沿线大地电位梯度小于2.5mV/m；缩短供电距离，能降低杂散电流干扰。

直流牵引供电系统 杂散电流 分层介质 扩散模型 影响因素

0 引言

城轨直流牵引供电系统中钢轨对地存在分布电阻，部分回流电流泄漏至大地并在牵引所附近流回整流机组负极，这部分电流被称为杂散电流[1-3]。杂散电流对埋地金属结构产生电化学腐蚀[4-5]。实际运行过程中，多牵引变电所并列运行，多列车移动负荷随时间动态变化，引起全线钢轨电位、杂散电流动态变化，造成地铁沿线附近地中电位不断波动，埋地金属结构受到的腐蚀也随之变化[6-8]。为了治理埋地金属结构的电化学腐蚀问题，需要确定杂散电流干扰范围和影响程度，并采取相应的防治措施。

文献[9-10]研究了地铁杂散电流场的分布规律及其影响范围，建立地铁杂散电流场数学模型，利用有限元分析在不同地质条件下的地铁杂散电流场，以上分析的杂散电流分布均是静态的，而实际的杂散电流随着列车位置的变化呈现动态波动的特征，有限元分析无法模拟杂散电流动态分布的特征，所以对评估杂散电流在地中的影响不具有全面性。文献[11]在杂散电流分布规律的基础上，利用CDEGS软件分析了不同牵引方式下不同位置地电位的影响和杂散电流的分布规律。文献[12]用数值计算的方法得到了地铁沿线杂散电流分布，并得出机车距牵引所负极越远，沿线杂散电流泄漏密度越大的结论。文献[11-12]只分析了杂散电流分布，缺少对地下环境的干扰判断。文献[13]在杂散电流电阻网络模型和电流场分布公式的基础上，提出基于地表电位梯度的地铁杂散电流动态干扰评估模型，该文献基于单列车双边供电情况进行计算，未考虑地铁线路多车多区间的情况。

本文研究多区间多列车情况下杂散电流对地铁沿线附近地下环境的影响范围和程度，推导多列车多区间杂散电流随时间动态变化的分布模型；考虑介质分层情况，采用叠加原理建立杂散电流在地中电位分布的模型，获得沿地铁线路附近地电位梯度动态变化的特征；通过CDEGS仿真验证分层介质中电位分布模型的准确性；结合实际线路的工程案例，分析杂散电流对地下环境的干扰，探讨过渡电阻、纵向电阻、介质电阻率、计算距离对地电位梯度的影响。

1 模型的建立

1.1 回流系统分布式电路与集中电路的等效过程

在实际运行线路中，多列车和多牵引变电所并列运行，供电系统处于多边供电状态。为了更加接近真实的运行状态，基于全线列车、变电所动态潮流计算结果，建立多区间多列车杂散电流动态分布模型，获得全线钢轨电位、杂散电流随时间动态变化的情况[5-6]。回流系统等效电路如图1所示。

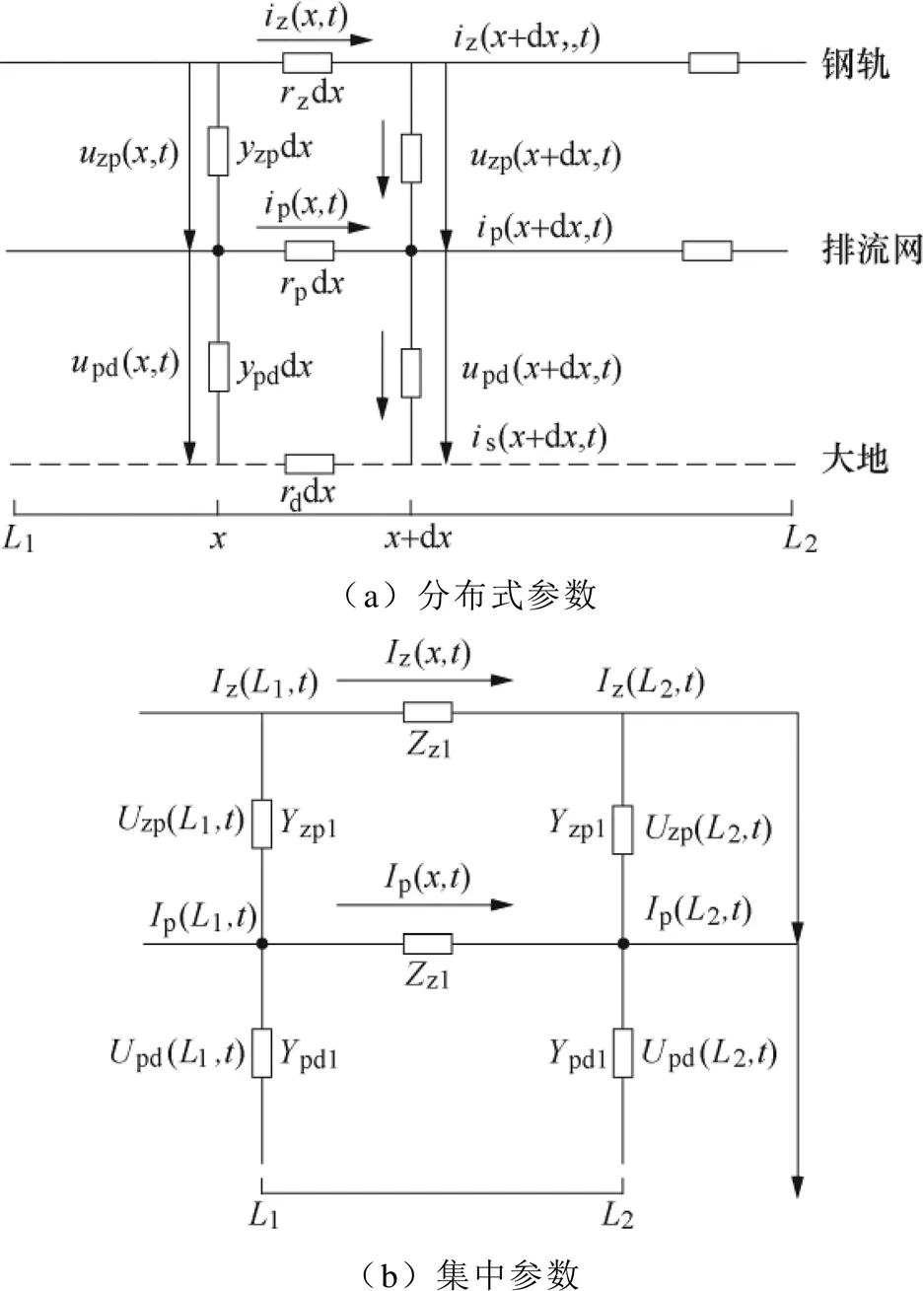
图1 回流系统等效电路

建立钢轨-排流网-地三层回流系统分布式微元等效电路如图1a所示。1为线路起点，2为线路终点，z为钢轨单位长度纵向电阻，p为排流网单位长度纵向电阻，zp为钢轨对排流网单位长度电导，pd为排流网对地单位长度电导，d为大地等效纵向电阻，杂散电流流入大地时，由于电流通道截面大，可认为大地的纵向电阻为零。

由基尔霍夫定律，可得

解式（1）所示的微分方程，可得

式中，zp为钢轨对排流网电位；pd为排流网对地电位；z为钢轨电流；p为排流网电流；1、2为特征值；1～4为待定系数，可根据边界条件得到；为系数矩阵，具体表达式为

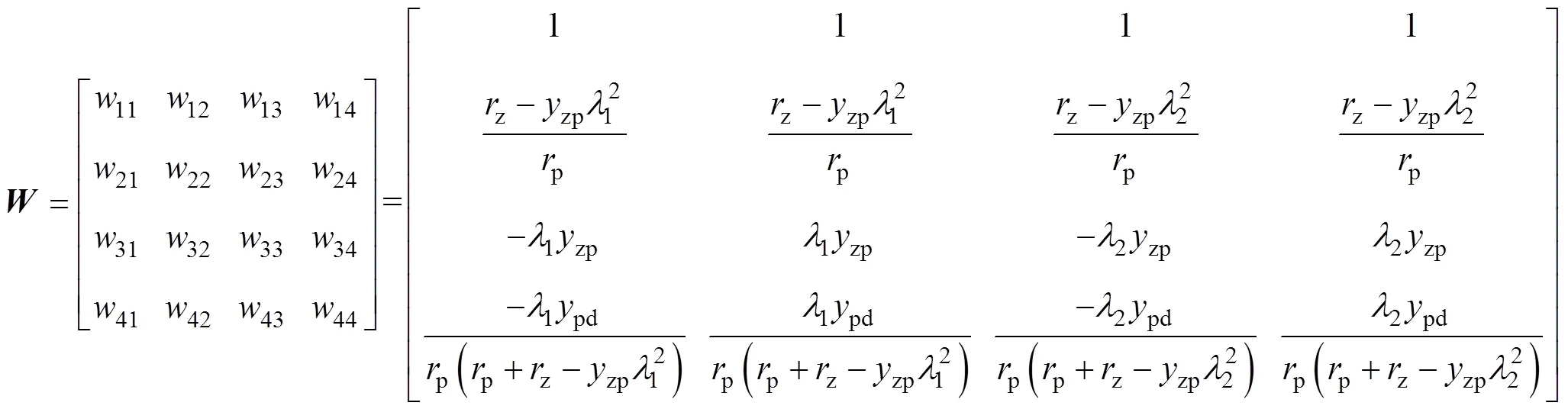
其中

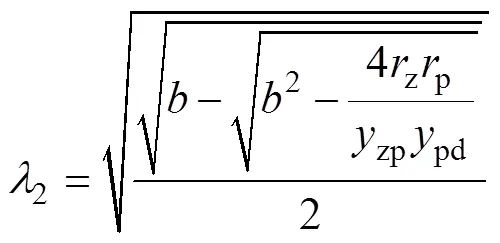
令

在分布式参数等效电路中，1处存在

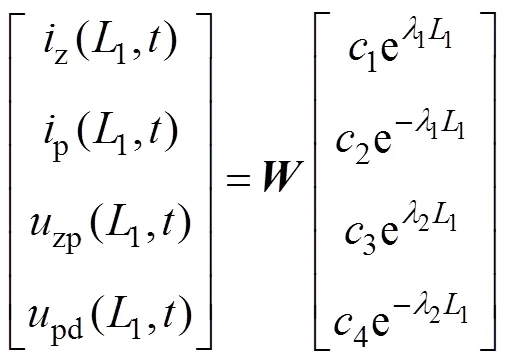
在2处存在

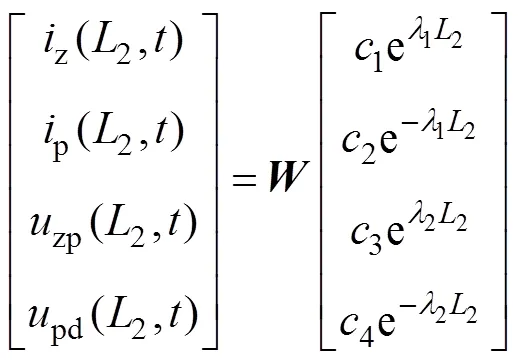
由式（4）、式（5）可推导出

由图1b可推导出

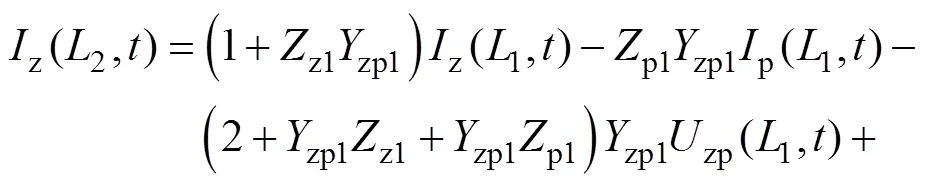
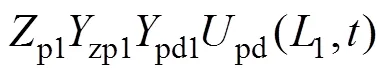
由等效原理可得，z(2,)=z(2,)，即可得到集中电路的结构参数为

由式（6）、式（8）可知，集中参数模型中各参数与被等效长度（1～2）和回流系统模型参数有关。基于系统潮流计算结果，可以得到回流系统参数动态分布。

1.2 杂散电流动态分布的计算过程

（1）将回流系统分布式模型转化为集中参数模型，建立牵引供电系统等效电路，如图2所示。线路起点为0，终点为，以列车或牵引所为节点分界面，L为第个节点位置，相邻两个节点为一个区间，共有+1个区间。列车等效为电流源t，0为整流机组电压，0为整流机组内阻。

图2 牵引供电系统等效电路

图2a中，回流系统分布式电阻网络与图1a一致，运用1.1节等效计算方法，将回流系统分布式电路等效为图2b集中式电路。图2b中，运用诺顿等效原理，将牵引所支路等效为电流源并联电阻模型，j(L,)、z(L,)、p(L,)为接触网、钢轨、排流网支路在时刻L处节点电压。jn为第段接触网等效电阻，zn为第段钢轨纵向等值电阻，pn为第段排流网纵向等值电阻，zpn为第个节点处钢轨对排流网等值电导，pdn为第个节点处排流网对地等值电导。

（2）在牵引供电系统集中参数模型下建立节点电压方程，进行潮流计算，可以得到任意时间和任意节点接触网电压j(L,)、钢轨电压z(L,)分布结果。当节点为牵引所时，钢轨注入电流z(L,)= (j(L,)-z(L,)-0)/0；当节点为列车时，注入电流z(L,)=t。

（3）基于牵引供电系统集中参数模型得到的钢轨节点注入电流，代入回流系统分布式参数计算杂散电流的动态分布。在时刻线路的起点和终点存在z(0,)=0；p(0,)=0；z(,)=0；p(,)=0；在时刻=L处有边界条件为

每个节点分界面存在4个连续边界条件，线路起点和终点存在4个边界条件，即每个区间均有4个边界条件，将式（9）代入式（2），联立4+4个方程求解，由此可以确定第个区间的4个待定系数c1, …, c4。

每个时刻均进行步骤（1）～（3），进而建立全线钢轨电位、杂散电流随时间动态分布结果为

式中，1,…,x1为在1,…,1个区间上的任意位置；s(,)为任意时刻和任意位置杂散电流的动态分布。

1.3 杂散电流在分层介质中的扩散模型

为了研究动态杂散电流对土壤环境产生的影响，提出杂散电流在介质中的扩散模型。钢轨通过绝缘块与紧固件放置在混凝土道床上，混凝土道床放置在土壤层，所以本次计算使用双层介质模型。地铁杂散电流在分层介质中的扩散模型如图3所示。第一层介质为混凝土层，钢轨置于混凝土层表面，排流网在混凝土层；第二层介质为土壤[14]。

由1.1节提出的多区间多列车杂散电流动态分布模型可得到全线杂散电流分布结果，本文杂散电流源为排流网向地中泄漏的电流。基于点电流源在分层介质中的地电位分布，采用叠加原理，可以得到全线杂散电流在任意位置的地电位分布。

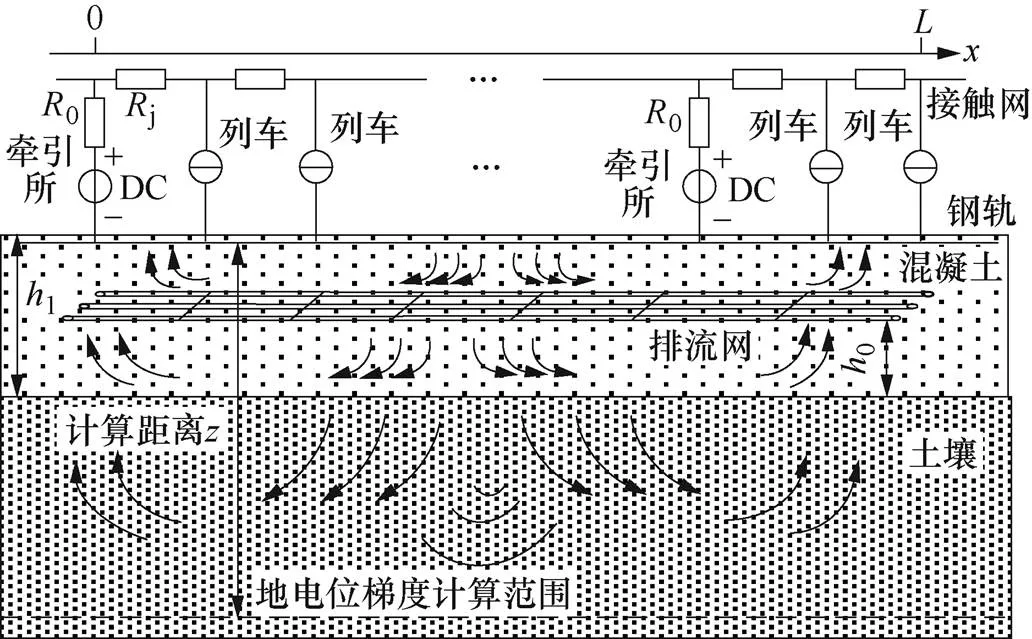
图3 杂散电流在分层介质中的扩散模型

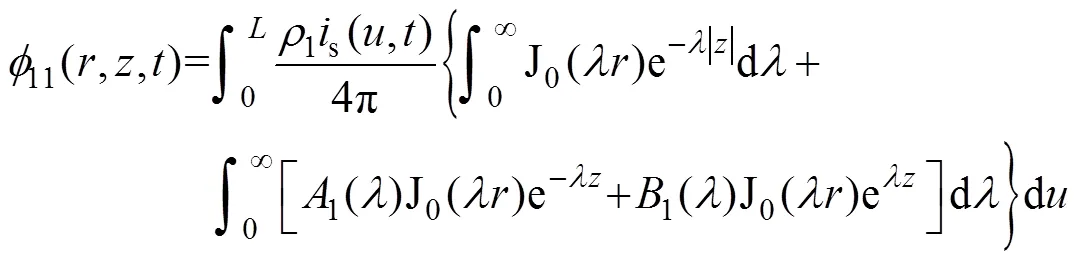
式中，1为混凝土电阻率（W·m）；s(,)为在时刻d长度上排流网向地中泄漏的电流（A）；J0(·)为第一类零阶贝塞尔函数；为所求电位点与泄漏电流点在水平方向上的距离（m），2=2+2；为计算距离（m）；1、1为待定系数。

式中，2为第二层土壤电阻率（W·m）；2、2为待定系数。

双层介质的电位分布边界条件为

式中，1为混凝土厚度（m）；0为排流网埋地深度（m）。

解式（11）和式（12）得待定系数的值为

排流网在混凝土层，即源点在混凝土层，计算土壤层的地电位分布。将2、2代入式（12）可得

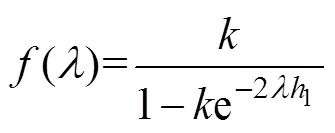
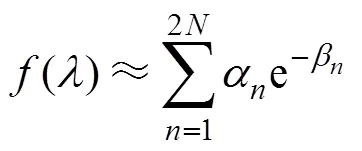
式中，、为待定系数，这两个值通常以共轭复数形式存在；为介质层数；为2倍介质层数。求出系数和之后，代入式（15）并进行李普希兹积分，可得杂散电流在土壤层中任意位置地电位分布的表达式为

其中

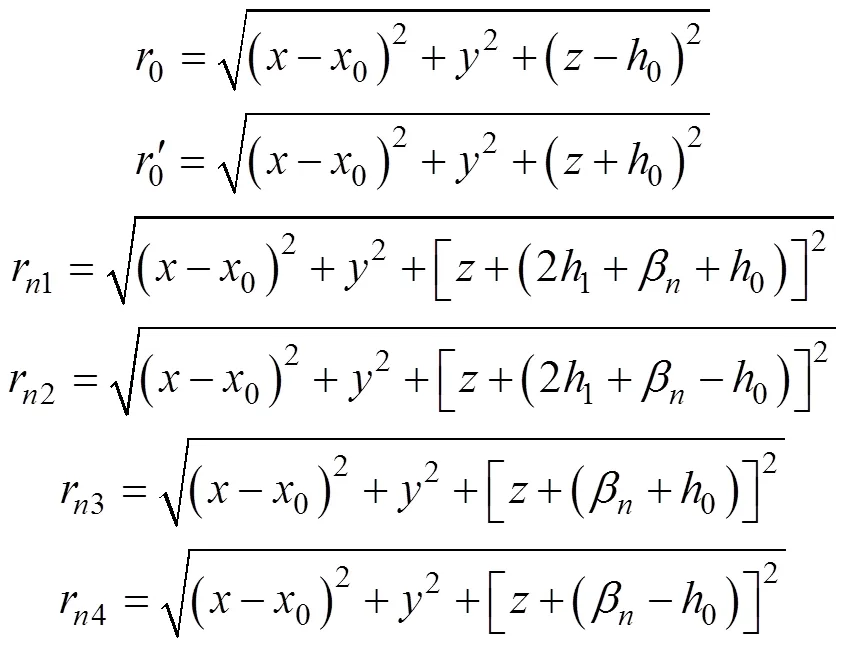
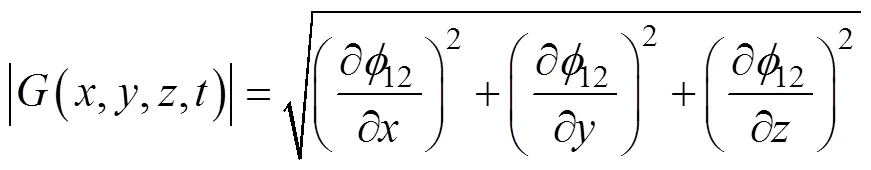
利用式（19）可求出地中任意位置的电位梯度。GB 50991[16]中提出地电位梯度作为杂散电流干扰程度的判断依据，则本模型的建立能够对运行线路杂散电流干扰程度提供定量的判断依据。

2 CDEGS仿真

为验证分层介质中地电位梯度分布模型的正确性，采用CDEGS软件的MALZ模块搭建单列车双边供电模型，钢轨和排流网分别等效为一根导体，列车与牵引所等效为电流源，介质水平分为两层，混凝土层厚0.6m，分析轨道正下方垂直距离20m处的电位分布情况，仿真计算示意图如图4所示。

图4 仿真计算示意图

本次仿真验证r1分别为0.3W·km、0.5W·km、1W·km，r2分别为0.03W·km、0.05W·km、0.1W·km，排流网埋地深度0.25m，h=0.6m，计算地深20m处地电位的分布，得到如图5所示的地电位分布。图5a为在r1=0.3W·km时，r2分别为0.03W·km、0.05W·km、0.1W·km的CDEGS仿真计算结果与推导的解析计算结果。图5b为在r1=0.5W·km时，r2分别为0.03W·km、0.05W·km、0.1W·km的CDEGS仿真计算结果与推导的解析计算结果。图5c为在r1=1W·km时，r2分别为0.03W·km、0.05W·km、0.1W·km的CDEGS仿真计算结果与推导的解析计算结果。

对地电位分布进行误差分析，误差均在8.66%以内，结果表明，采用分层介质地电位模型计算地电位梯度是有效的。

3 案例分析

3.1 地铁线路情况

本小节以国内某地铁线路为例分析地铁沿线附近杂散电流对土壤环境的影响。列车采用6辆编组B型车，最高速度80km/h。线路全长25.4km，共设置10个牵引变电所，其中有两个区间所。全线共有9个车站，车站与牵引所的相对位置如图6所示。全线设置了3套逆变回馈装置，分别位于第1个牵引所和最后两个牵引所。前两套的容量为2MW，最后一套的容量为3MW。

图6 车站与牵引所位置

直流牵引供电系统的参数见表1。实测得到的上下行列车位置-取流曲线如图7所示。

表1 系统参数设置

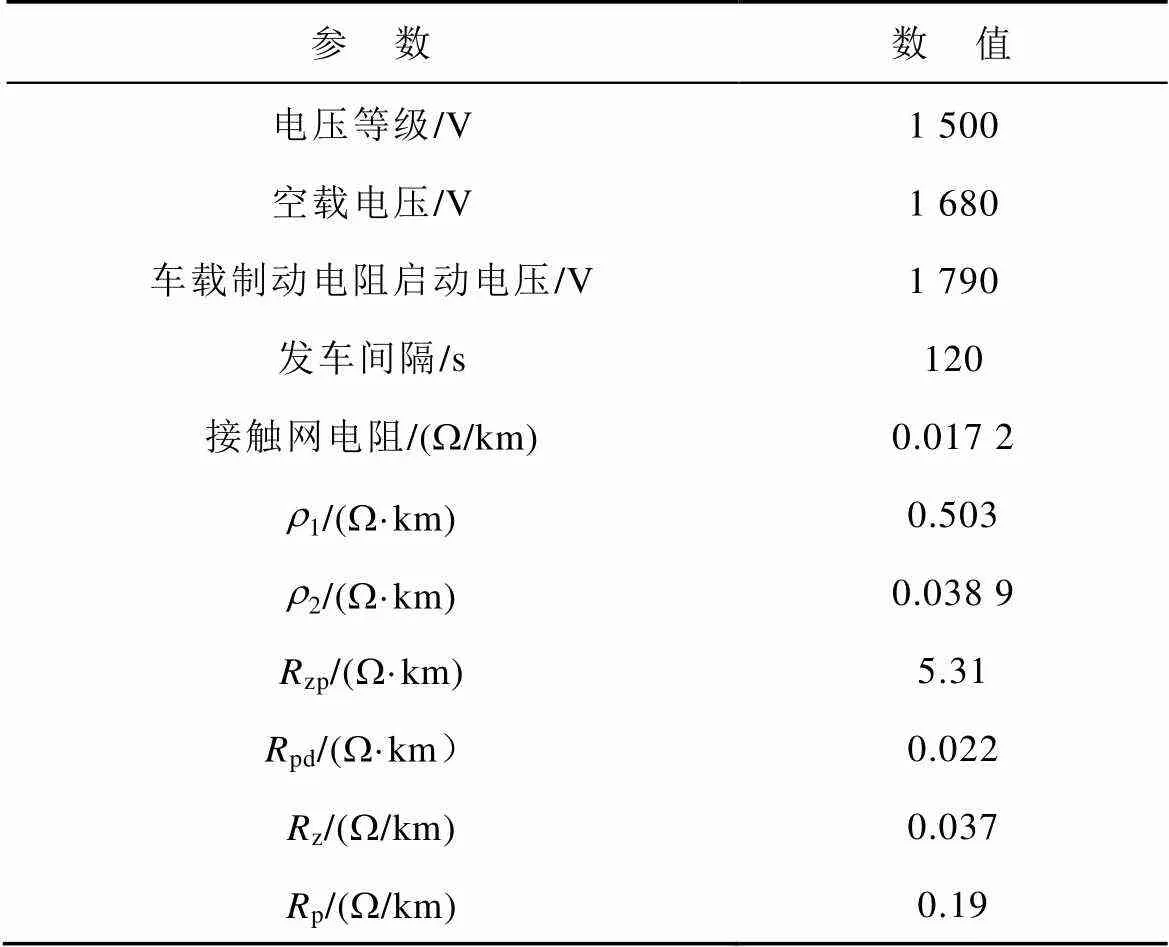
Tab.1 system parameter setting

3.2 杂散电流干扰程度和范围分析

基于系统潮流计算结果，利用第1节推导的多区间多列车钢轨电位动态分布模型，得到如图8所示的全线钢轨电位随时间变化的动态分布。由图8可知，全线钢轨电位随着时间的变化正负不断波动，波动范围为-54.23～78.46V。

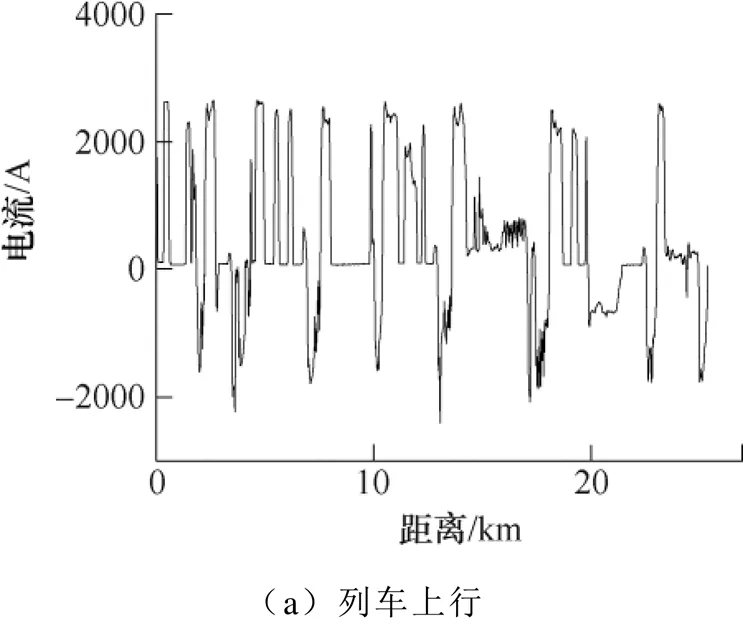
图8 钢轨电位动态分布

根据CJJ/T 49-2020[17]中5.4.4节提出，穿越江、河、湖、海及沼泽地带的隧道和线路交叉跨越点50m区域内的地铁主体建筑结构，应采取加强绝缘的防护措施。所以本次计算范围为轨道垂直距离50m，平行于钢轨的方向，得到如图9所示的平行于钢轨方向的地电位梯度分布。由图9可知，在地铁运行过程中，同一位置地电位梯度大小随着时间不断变化。其原因是，列车的位置与取流随着时间不断变化，全线杂散电流在变化，引起地电位梯度不断波动。

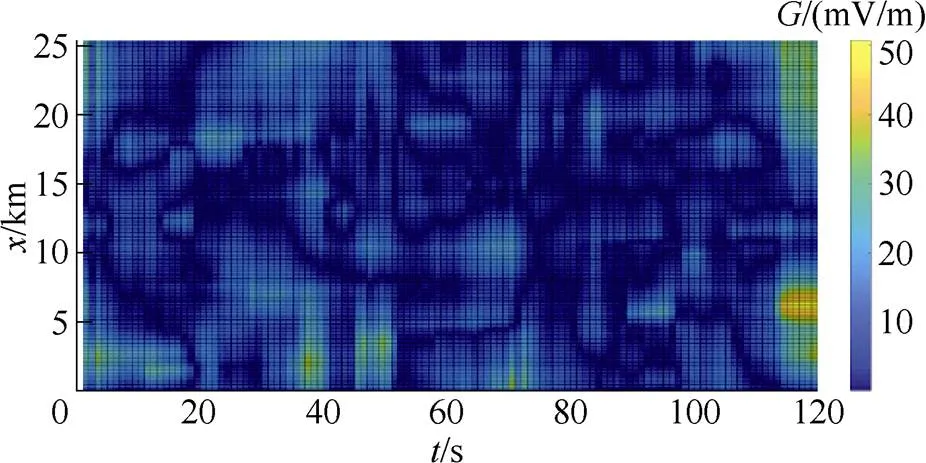
图9 地电位梯度分布

按照式（21）计算全线每一处位置在运行时间内的平均地电位梯度，本条线路的结果如图10所示。

当地电位梯度大于等于2.5mV/m时，直流杂散电流的干扰严重；地电位梯度在0.5～2.5mV/m内，存在直流杂散电流的干扰[16]。由图10可知，全线地电位梯度的范围为3.525～12.7mV/m，全线区段杂散电流干扰严重。在15km附近地电位梯度较低，原因在于13.9km处和15.6km均有牵引所，两所之间供电距离较短。

4 探讨影响地电位梯度的因素

根据第2节推导的多区间多列车杂散电流在分层介质中地电位分布模型可知，地电位分布取决于过渡电阻、纵向电阻、混凝土电阻率、土壤电阻率及计算深度等参数。为了探究各参数对地电位梯度的影响程度，以第3节地铁实际运行情况为例讨论地电位梯度分布，本文讨论采用单一变量原则，每次只改变讨论的参数，其他参数均不变。

4.1 过渡电阻对地电位梯度的影响

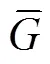
4.2 纵向电阻对地电位梯度的影响

图11 Rzp与的关系

图12 Rz与的关系

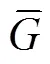
图13 Rp与的关系

4.3 r1对地电位梯度的影响

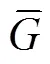
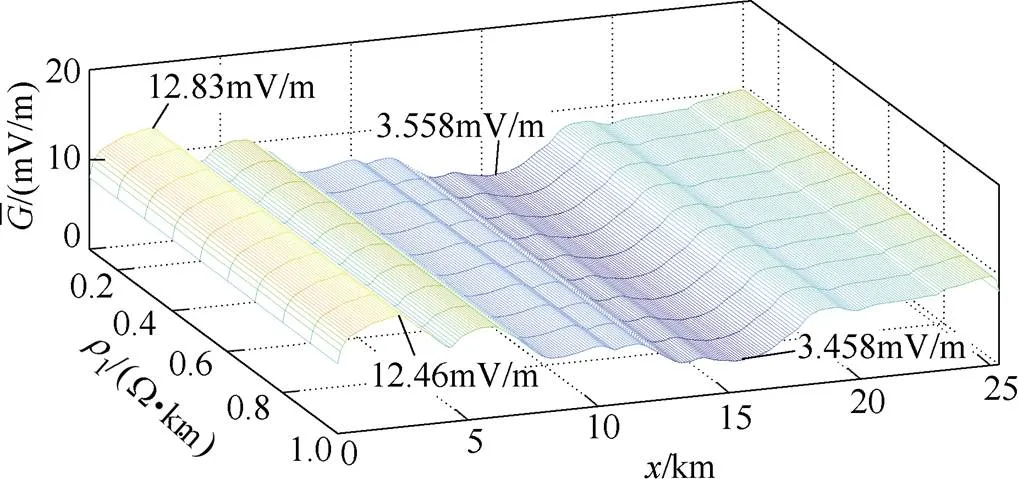
图14 r1与关系

4.4 r2对地电位梯度影响

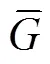
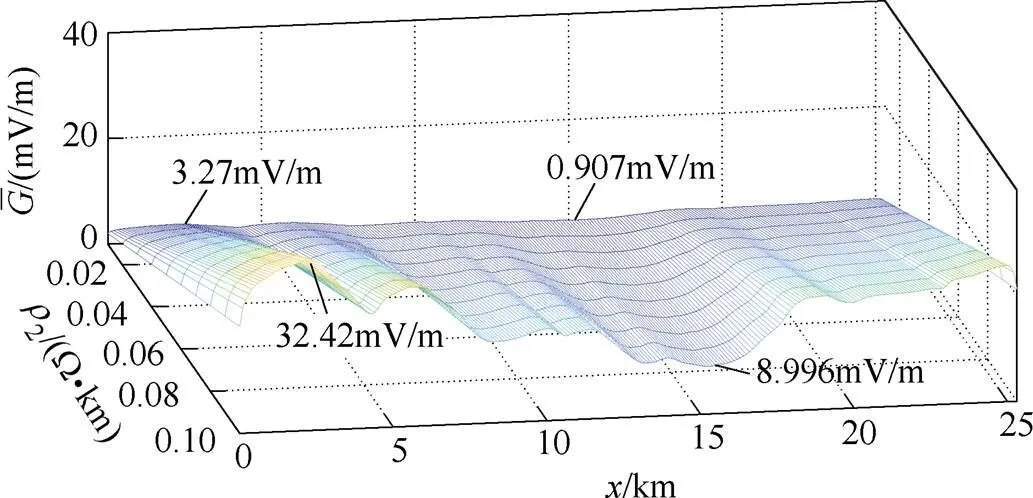
图15 r2与的关系

4.5 z对地电位梯度的影响

图16 z与的关系

5 结论

1）本文建立了直流牵引供电系统动态杂散电流在分层介质中的扩散模型。将回流系统分布式电路等效为集中电路，建立牵引供电系统集中等效电路，采用节点电压法，进行系统潮流计算，基于潮流计算结果，建立全线杂散电流随时间动态分布模型；基于点电流源在分层介质中的地电位分布模型，采用Prony法进行求解；采用叠加原理建立杂散电流在层状介质中的扩散模型，与CDEGS仿真结果进行对比，误差范围在8.66%以内，说明模型是有效的。

[1] Tzeng Y S, Lee C H. Analysis of rail potential and stray currents in a direct-current transit system[J]. IEEE Transactions on Power Delivery, 2010, 25(3): 1516-1525.

[2] Dolara A, Foiadelli F, Leva S. Stray current effects mitigation in subway tunnels[J]. IEEE Transactions on Power Delivery, 2012, 27(4): 2304-2311.

[3] 王慧康, 杨晓峰, 倪梦涵, 等. 轨道电位与杂散电流动模实验平台[J]. 电工技术学报, 2020, 35(17): 3609-3618.

Wang Huikang, Yang Xiaofeng, Ni Menghan, et al. Experimental platform for orbital potential and stray current flow mode[J]. Transactions of China Electro- technical Society, 2020, 35(17): 3609-3618.

[4] 孟晓波, 曹方圆, 廖永力, 等. 抑制直流接地极影响的管道绝缘防护措施分析[J]. 高电压技术, 2017, 43(12): 3900-3906.

Meng Xiaobo, Cao Fangyuan, Liao Yongli, et al. Analysis of pipeline insulation protection measures to suppress the influence of DC grounding electrode[J]. High Voltage Engineering, 2017, 43(12): 3900-3906.

[5] 杜贵府, 张栋梁, 王崇林, 等. 直流牵引供电系统电流跨区间传输对钢轨电位影响[J]. 电工技术学报, 2016, 31(11): 129-139.

Du Guifu, Zhang Dongliang, Wang Chonglin, et al. Effect of traction current transmission among power sections on rail potential in DC mass transit system[J]. Transactions of China Electrotechnical Society, 2016, 31(11): 129-139.

[6] Du Guifu, Wang Jun. Evaluation of rail potential and stray current with dynamic traction networks in multi-train subway systems[J]. IEEE Transactionson Transportation Electrification, 2020, DOI: 10.1109/ TTE.2020.2980745.

[7] 杨晓峰, 薛皓, 郑琼林. 基于双向可变电阻模块的杂散电流与轨道电位动态模拟系统[J]. 电工技术学报, 2019, 34(13): 2793-2805.

Yang Xiaofeng, Xue Hao, Zheng Qionglin. Stray current and rail potential dynamic simulation system based on bidirectional variable resistance module[J]. Transactions of China Electrotechnical Society, 2019, 34(13): 2793-2805.

[8] 蔡力, 王建国, 樊亚东, 等. 地铁走行轨对地过渡电阻杂散电流分布的影响[J]. 高电压技术, 2015, 41(11): 3604-3610.

Cai Li, Wang Jianguo, Fan Yadong, et al. Influence of the track-to-earth resistance of subway on stray current distribution[J]. High Voltage Engineering, 2015, 41(11): 3604-3610.

[9] 胡云进, 钟振, 方镜平. 地铁杂散电流场的有限元模拟[J]. 中国铁道科学, 2011, 32(6): 129-133.

Hu Yunjin, Zhong Zhen, Fang Jingping. Finite element simulation of subway stray current field[J]. China Railway Science, 2011, 32(6): 129-133.

[10] 王果, 裴潇湘. 地铁常用隧道杂散电流场三维有限元模拟[J]. 铁道科学与工程学报, 2014, 11(6): 85-91.

Wang Guo, Pei Xiaoxiang. Three dimensional finite element simulation of stray current field in common subway tunnels[J]. Journal of Railway Science and Engineering, 2014, 11(6): 85-91.

[11] Wu Guoxing, Wang Peng, Li Junyi, et al. Influence of stray current on ground potential distribution of urban rail transit[C]//2019 IEEE Sustainable Power and Energy Conference (iSPEC), Beijing, China, 2019: 2227.

[12] 王爱民, 林圣, 李俊逸, 等. 城市轨道交通长线路杂散电流仿真模型[J]. 高电压技术, 2020, 46(4): 1379-1386.

Wang Aimin, Lin Sheng, Li Junyi, et al. Simulation model of stray current in long line of urban rail transit[J]. High Voltage Engineering, 2020, 46(4): 1379-1386.

[13] 王禹桥, 黄玉坚, 彭成宽, 等. 基于地表电位梯度的地铁杂散电流动态干扰范围评估模型[J]. 北京交通大学学报, 2020, 11(6): 85-91.

Wang Yuqiao, Huang Yujian, Peng Chengkuan, et al. An evaluation model for the dynamic interference range of subway stray current based on surface potential gradient[J]. Journal of Beijing Jiaotong University, 2020, 11(6): 85-91.

[14] 朱峰, 李嘉成, 曾海波, 等. 城市轨道交通轨地过渡电阻对杂散电流分布特性的影响[J]. 高电压技术, 2018, 44(8): 2738-2745.

Zhu Feng, Li Jiacheng, Zeng Haibo, et al. Influence of rail-to-earth resistance of urban transit system on distribution characteristics of stray current[J]. High Voltage Engineering, 2018, 44(8): 2738-2745.

[15] 李中新, 袁建生. 变电站接地网模拟计算[J]. 中国电机工程学报, 1999, 19(5): 76-79.

Li Zhongxin, Yuan Jiansheng. Simulation calculation of substation grounding grid[J]. Proceedings of the CSEE, 1999, 19(5): 76-79.

[16] GB 50991-2014 埋地钢质管道直流干扰防护技术标准[S]. 北京: 中国计划出版社, 2015.

[17] CJJT 49-2020 地铁杂散电流腐蚀防护技术标准[S]. 北京: 中国计划出版社, 2020.

Diffusion Model of DC Dynamic Stray Current in Layered Soil

11211

（1. School of Electric Engineering Southwest Jiaotong University Chengdu 610031 China 2. Beijing National Railway Communication Signal Research and Design Institute Group Co. Ltd Beijing 100071 China）

In order to study the interference range and influence degree of the stray current of the DC traction power supply system, the distributed circuit of the return system was equivalent to a centralized circuit. The node voltage method is used to calculate the system power flow. Accordingly, a dynamic distribution model of the stray current over time was established, andthe diffusion model of dynamic stray current in layered media was established by the superposition principle. The Prony method was used to solve the model. Compared with the simulation results of CDEGS software, the ground potential calculation error was within 8.66%. A domestic subway line adopts 6B grouping, the maximum speed is 80km/h, the departure interval is 2min, the concrete resistivity is 0.503W·km, and the soil resistivity is 38.9W·m. When the distance between the buried metal structure and the subway line is 50m, the rail transition resistance value is increased to more than 40W·km, or when the rail transition resistance value is 5.31W·km, the distance between the buried metal structure and the subway line is increased to more than 0.25km, and the ground potential gradient along the line is less than 2.5mV/m, which means shortening the power supply distance can reduce stray current interference.

DC traction power supply system, stray current, layered medium, diffusion model, influencing factors

10.19595/j.cnki.1000-6753.tces.210025

TM922

国家重点研发计划（2017YFB1201103-05）和基于车-地-轨耦合的杂散电流评估与控制技术（2017YFB1201103-05）资助项目。

2021-01-07

2021-05-16

刘 炜 男，1982年生，副教授，博士生导师，研究方向为杂散电流、牵引供电系统设计仿真和再生制动能量利用。E-mail: liuwei_8208@swjtu.cn

潘卫国 男，1980年生，高级工程师，研究方向为牵引供电系统设计及智能铁路供电系统。E-mail: panweiguo@crscd.com.cn（通信作者）

（编辑 陈 诚）