数形结合思想在高中物理解题中的应用
刘 丽
(云南省曲靖市罗平县第一中学 655800)
在解决物理问题时,数形结合思想是一种很有效的思想方法,高中物理教师在日常教学活动中,可以从学生的实际情况入手,培养学生的数形结合思维,指引学生通过数形结合的方式对复杂的物理问题进行简约化处理,便于学生理清解题思维.很多时候,有的物理问题在文字描述上比较模糊,但是利用图形,则可以很直观的了解到相应关系,对此教师要引导学生学会用数形结合来灵活的处理问题.
一、高中物理解题与数形结合的关联
数形结合简单来说就是数据和图形之间的相互关系.高中物理教师在引导学生解决物理问题时,可以学生指引借助数形结合的方式,对题目中的条件进行分析,找出适宜的解题方式,完成高效解题.在实践中,数形结合是一种很有效的解题工具,能很好的消除学生恐惧物理的情况.有的学生会觉得物理问题抽象,理不清相关数量关系,而数形结合思维可以帮助学生直观的梳理问题,能促使学生在解题中做到数、形转变,便于学生形象化处理物理问题.数形结合思维的最大特征在于其本身十分清晰、直观,与高中生本身的认知特点相互契合,并且和传统的物理解题教学相比较,数形结合这种方式能显著激活学生本身的主动性,让学生自觉的寻找物理解题点,这对于学生物理思维形成有很大帮助.此外,对于物理基础比较差的学生来说,他们在遇到一些难度比较大的物理题时,会产生退缩心理,不知道该如何下手,这必然会影响到学生物理学习效果提升.所以高中物理教师可以指引学生从数形结合的角度对问题进行思考,探寻新的解题思路,找准问题考点,强化对知识的感知.
二、高中物理解题应用数形结合的方法
1.用数解形
高中生在解物理题时,经常会看到题目中给出各种复杂的代数关系,学生在分析题时会感觉很迷惘,不知道如何入手.对此物理教师可以指引学生改变自己的思维,借助数形结合,利用形象的图形来分析复杂的数量关系,然后对题目进行简化,完成解题.
例如:百米运动过程中一个计时员在听到枪响后,开始记录运动员的百米赛跑成绩.该计时员看到第一个运动员到达终点后,得出该运动员的百米赛跑成绩是12.2s,问这种计时方法准确吗?如果这种方法不准确,该采取什么样的方法进行计时?该运动员的百米赛跑正确时间应该是多少秒?
根据题目中的信息,简单的画出一个图形,如图1.AB代表运动员的百米赛跑跑道,A、B分别是起点和终点.持枪的人与运动员一起站在A点位置,但是计时员是站在B点位置.忽视运动员本身的反应时间,那么枪响与运动员起跑是同一时间进行,但是枪声传到B点则有一段时间,并且在这段时间里运动员已经跑了一定距离.从这一角度看,计时员本身采用的计时手段是错误的.事实上学生结合自己的实践生活可以知道,在百米赛跑中计时员一般都是根据自己看到枪响冒出的烟开始计时的,其主要原因在于光在空气的传播速度要比声音快.
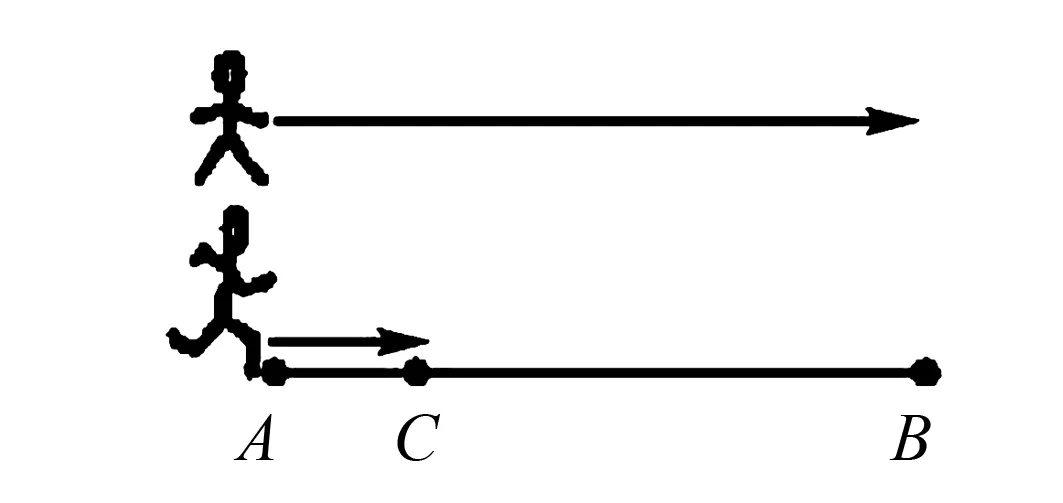
图1
2.以形转数
高中物理考试中,有时候题目会直接给出图像,包括运动状态图、实物图等,但是题目并没有给出详细的数据信息,这就需要学生对图形进行认真观察分析,找出相应的数据关系,然后进行计算.
例如:公路上行驶有一辆拉货车,某时刻开始记录,该货车的发动机功率P和时间的关系如图2,假设该货车在行驶期间受到的阻力f是固定不变的,那么图3中,哪一个最有可能是货车速度与时间变化图?
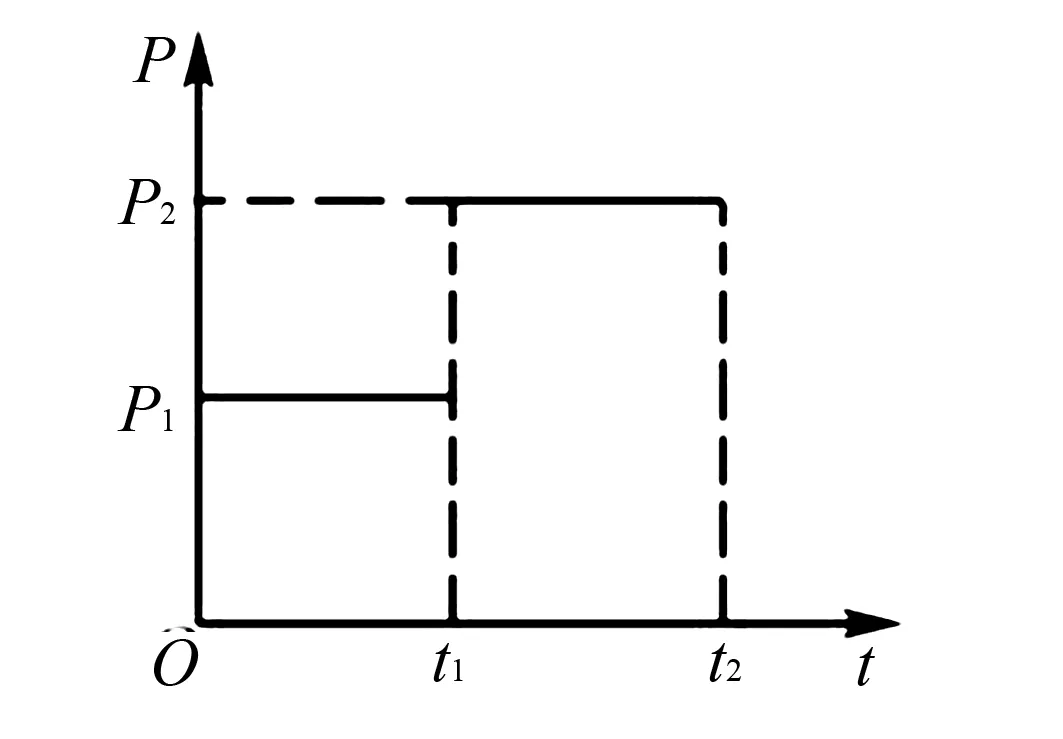
图2
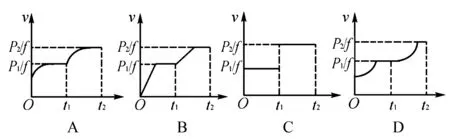
图3
3.数形互补
对高中物理问题进行仔细分析可以看出,有一部分习题具有很强的综合性,学生必须综合应用数形结合来寻找解题思路.对此,在实践教学中,高中物理教师要指引学生学会对物理题目进行进行综合分析,根据题目已知信息,找出图形、数量之间的关系,综合应用数形结合来实现解题.
例如:一个长木板在水平面上运动,t=0时,有一个静止物体被放到木板上方,接着长木板的运动时间和运动速度之间的关系如图4所示.如果静止物体的质量等于长木板的质量,同时水平面、长木板、静止物体之间都存在摩擦力,而静止物体与长木板的最大静摩擦力和滑动摩擦力相等,在整个运动期间,物体都保持在木板上.问长木板和物体的动摩擦因数是多少?长木板和水平面的动摩擦因数是多少?
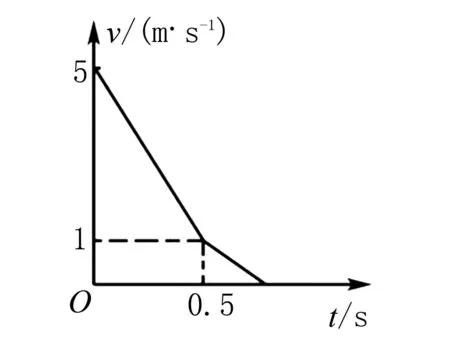
图4
在本题中,要先对小物块和长木板进行受力分析,从而得出它们的运动情况.在0s至0.5s阶段,长木板和物体间、长木板和地面间均有摩擦力,从而小物块做匀加速运动长木板做匀减速运动直到0.5s时它们的速度相等.该阶段对小物块用加速度的定义式算出其加速度的大小,再根据牛顿第二定律便可算出小物块和长木板之间的动摩擦因数.其次通过计算图4中0s至5s图像的斜率,便可得出长木板的加速度,最后再对长木板用牛顿第二定律,从而求出长木板和水平面间的动摩擦因数.本题解题的关键,重在引导学生正确画出受力分析图,然后得出物体的运动状况,然后理清自己的解题思路,最后列方程完成题目求解.高中物理教师要引导学生在解题中,学会借助图形来分析物理规律,并且图形能更加直观的展现出相关物理特征,如在本题中,借助图形能更好判断物体运动状态,在此基础上列出方程完成计算.
综上所述,高中物理教师在日常教学中,要充分培养学生的数形结合思维,指引学生可以借助数形结合的方式来明确物理解题方法,从而更加高效、准确的完成物理解题,以此满足学生的学习需求.

