微课在高中数学教学中的运用策略
柏鹏鹏
(江苏省如东县马塘中学 226401)
计算机技术的发展将人们带入了信息化时代,“读屏”似乎已经成为了人们每天都会做的事情,手机、电脑设备的普及,更是为信息的快速、高效传播提供了更加便利的条件,微课作为一种以视频、音频、图片结合的教学方式应运而生.与传统的教学相比,微课借助音频、视频以及文字结合的方式,将所传达的信息更加生动形象地展示了出来,可以让学习者通过更为直观的视觉观察理解知识点,凸显出学习主题的内容,也成为了教师课程教学中的有利辅助工具.但是,因为微课是近年来兴起的一种新型教学方式,许多教师并没有掌握微课在学科教学中的有效运用方法,因此导致微课的实践教学效果大打折扣,甚至有不少教师对微课在课堂教学中的运用产生怀疑,这些问题迫切地需要解决,也是本文研究的重点内容.
一、微课在课前预习教学中的运用
良好的预习习惯养成对于高中生的数学学习是有百利而无一害的,但是通过对高中生现阶段的数学预习情况来看,许多学生虽然能够意识到预习学习的重要性,但是却又面临着不会预习的难题.在传统的高中数学教学中大部分教师的预习学习任务布置比较笼统,又无法做到课前预习的一对一指导,因此导致高中生的预习学习目标不清晰,预习学习效果不高.而微课在课前预习教学中的运用,就可以很好地解决教师课前预习指导的难题,通过师生互动平台为学生传送预习学习指导的信息,让学生可以在课下的时间观看内容,为高中生的数学课前预习指明了方向的同时,也大大地提升了学生的预习学习效率,明确了本节课要学习的重要知识点有哪些,促使学生在预习中初步理解重要数学知识点,让高中生接下来的课堂学习有所侧重.
以《任意角的三角函数》为例,首先,教师制作的预习微课件中向学生展示了在高中数学必修一课本已经学习过的函数概念,函数的数学表达式、定义域、值域以及函数值变规律,指数函数的图像与性质,对数函数的图像与性质,幂函数的图像与性质,之后微课件中展示一个不完整的表格,表格中是几种幂函数y=x、y=x2、y=x3、y=x-1等,要求学生们将对应函数的定义域、值域、奇偶性、单调性、定点等内容补充完整.继续呈现出学生在初中阶段学习的锐角三角函数定义,梳理出在直角三角形ABC中,sinA=∠A的对边÷斜边,cosA=∠A的邻边÷斜边,tanA=∠A的对边÷∠A的邻边.最后引出本节课学习的任意三角函数预习重点知识点,让学生可以在教师所制作的课前预习指导课件中明确“任意角的三角函数”课前学习需要从三角函数的定义、定义域、值的各象限的符号以及公式几个方向入手,在预习学习中梳理出这些基本知识点,以提升学生的预习学习目的性.
二、微课在知识理解教学中的运用
与初中数学不同,高中阶段的数学课本中被纳入了许多抽象难懂的数学概念,微课在高中生数学概念性知识理解中的运用,可以起到将抽象数学知识转化为更为具体的、直观的数学图形或画面等方式,以帮助学生理解数学抽象知识点.
以《任意角的三角函数》这节课中学生们普遍难理解的“三角函数线”的概念教学为例,这节课中的“三角函数线”概念讲解需要学生认清三角函数线的概念,适应从“数”到“形”的过渡,并理解正弦线、余弦线、正切线等概念定理.譬如,在“正弦线”的知识点讲解中,教师可以利用微课展示如图一的内容,并讲解到:“如图一所示,角ɑ终边与单位圆交于点P,过点P做x轴的垂线,垂足于点M,则sinɑ=MP/OP=MP(OP=1).MP即为角ɑ的正弦线,MP的长度为sinɑ的绝对值,MP的方向为sinɑ的正负.在正弦线的概念讲解之后,教师应提出问题引领学生思考:“你能用正弦线分析不同象限角对应的正弦函数值的符号吗?”要求学生对问题分析并展开讨论,利用三角函数线的概念分析让学生理解正弦线在各象限中的符号.
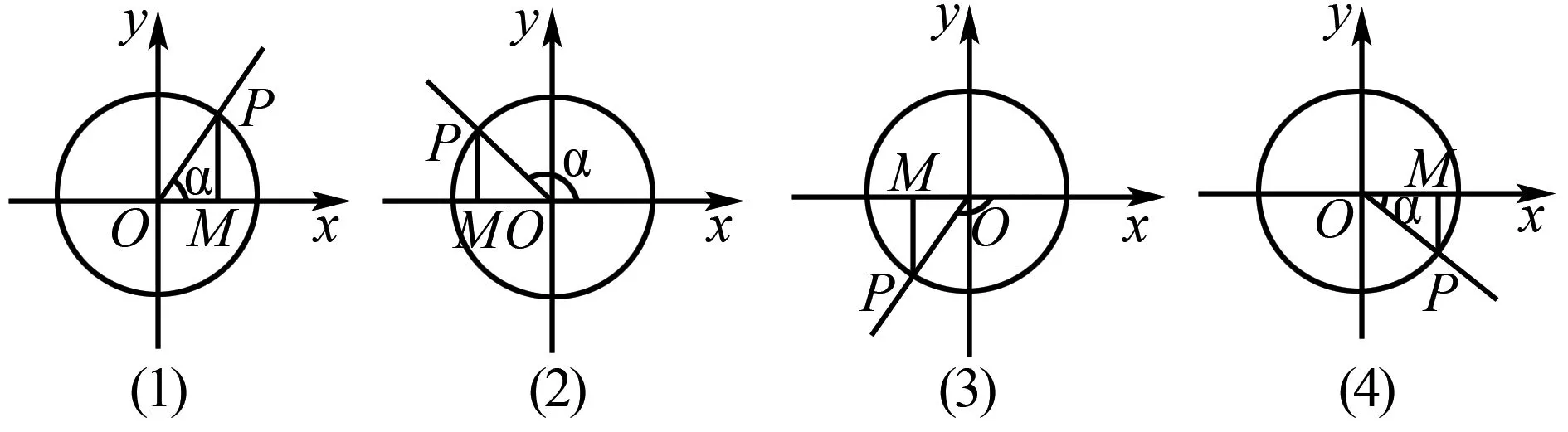
图1
接下来,教师利用微课展示图二中的内容,并要求学生通过图二中给出的信息,完成用正弦线分析正弦函数定义域与值域的问题,这样不仅可以深化学生对三角函数线概念的理解,也培养了学生利用三角函数线解释正弦函数定义域、值域的能力.
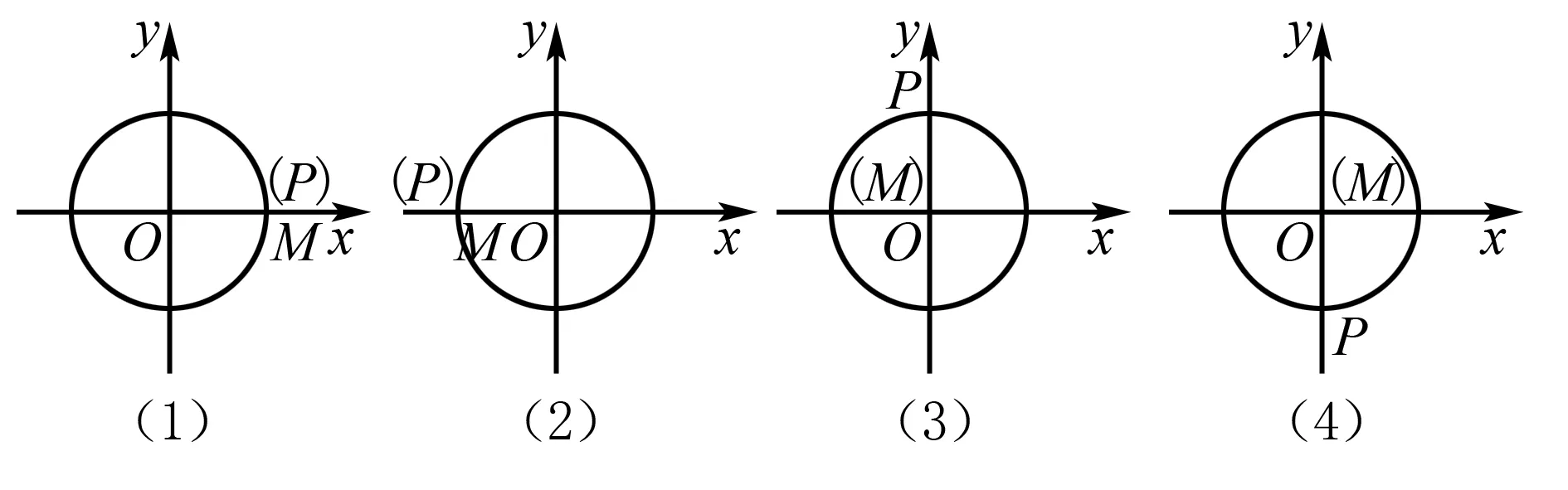
图2
余弦线以及正切线的概念讲解同样可以利用这种方法,但是需要注意的是在知识理解型的微课课件制作中教师要做到三点:第一,针对性强;第二,知识点讲清、讲透;第三,避免过程过于繁琐,从而让高中生能够通过微课的视频观看,掌握三角函数线的概念,深化对数学抽象知识点的理解与吸收程度.
三、微课在疑难解题教学中的运用
习题解答是高中生数学学习中的有一个难点,许多的学生在数学问题的解答中会出现无法找到突破口的问题,有时对于教师所讲解的习题解答方法也是一知半解,而课堂的教学时间有限,教师不可能将每一名学生没有掌握的习题解答点全部重复地讲解一遍或多遍,学生在课下的时候,也缺乏与其他学生主动讨论的积极性,长期以往学生的解题疑惑点无法得到有效的解决,就会越积越多.为了解决这种问题,教师可以利用微课,将课堂中的习题讲解过程录制成视频课件,并在下课后传送到学生的移动终端学习设备中,这样学生们就可以根据自己的学习疑惑点选择重复性地观看教师的习题讲解视频片段,做到及时地课下补救.
以经典题型“三角形解的个数示例”为例,教师可以提出这样的问题:“假设在△ABC中,∠A、∠B、∠C所对的边分别为a、b、c,已知a、b、∠A(∠A为锐角),讨论三角形解的个数.”教师可以组织学生以小组为单位探索三角形解的个数是多少,不同的学习小组可以提出自己的解题方法以及得出的三角形解的个数,譬如:A小组采取了数形结合的方法,得出当a 总之,微课在高中数学教学中的运用,符合教育信息化发展的需求,也为教师提供了有力的教学辅助工具,有助于打破传统教学模式的局限性,弥补了教师无法对学生的课前预习、课后练习复习指导的问题,也丰富了课堂教学手段.因此,高中数学教师应善于运用微课开展数学教学活动,将微课巧妙地融入到各个教学环节之中,更好地发挥出微课的教学优势,促进高中数学教学质量的提升.

