基于离散教与学算法的分布式预制流水车间调度研究

曹劲松，熊福力

(西安建筑科技大学 信息与控制工程学院，西安 710055)

0 引言

流水车间调度问题(FSSP, flow shop scheduling problem)已被证明是一个非确定性多项式难(NP-hard)问题[1-2]，问题解空间大，复杂度高，传统的精确算法如分支定界[3]在求解该类问题时，很难在合理时间内得出问题解。因此，研究人员通常采用启发式算法对相关问题进行求解。潘子肖和雷德明[4]针对分布式低碳并行机调度问题提出了一种基于问题性质的非劣排序遗传算法-II。Abdel等[5]提出了一种将鲸鱼优化算法与局部搜索策略相结合的新算法来解决置换流水车间调度问题。刘晶晶等[6]根据柔性作业车间调度问题的特点，以最小化完工时间为目标提出了一种混合果蝇-遗传算法，并与遗传算法对比，证明了所提算法的有效性。近年来，更多的智能方法被应用于FSSP，如模拟退火[7]、禁忌搜索[8]、蚁群算法[9]、粒子群优化[10]、免疫算法[11]、人工蜂群算法[12]等。

2011年，Rao等[13-15]从实际的教师教学和学生的学习过程中得到启发，提出了一种新型的群智能算法-教与学优化算法(TLBO,teaching-learning based optimization)，该算法具有收敛速度快，能够屏蔽参数干扰的优点。而后，赵乃刚[16]将其应用在求解无约束优化问题上。马文强等[17]设计了一种混合教与学算法有效求解了炼钢连铸调度问题。何雨洁等[18]提出了一种混合离散TLBO算法求解复杂并行机调度问题。但目前关于TLBO算法的研究集中在求解线性化问题上，仅少部分学者将其应用在FSSP领域，且通过TLBO算法解决分布式预制构件流水车间调度问题的研究还未出现。

因此，本文在充分考虑预制构件生产特殊性(工序间的差异性较大，工序处理周期长)的基础上，针对分布式预制构件流水车间调度问题，以最小化订单总拖期惩罚为目标，结合问题双层整数编码的特点，提出了一种离散教与学优化算法(DTLBO)。最后通过大量算例的测试实验，验证了DTLBO算法求解问题时的有效性。

1 问题描述与建模

如图1所示，分布式预制流水车间调度问题可以描述为：来自客户的n个预制构件订单，需被指派到F个预制构件工厂处理，每个工厂内都有一条流水线，流水线上的机器配置相同。生产过程由6道工序组成：1)模具组装；2)钢筋预埋；3)混凝土浇筑；4)蒸汽养护；5)模具拆除；6)瑕疵修整。每道工序仅有一台机器(即单生产线工作模式)。预制构件生产不同于传统流水车间问题，根据生产工艺的特征可将工序分为并行工序(可同时处理多个订单)和串行工序(当进行到该工序下的订单未处理完前，不可对下一订单进行处理)。其中工序4蒸汽养护为并行处理，其余工序为串行处理。若订单j被指派到工厂f生产后，在交货期dj后完工，则会产生拖期惩罚费用。研究以最小化总订单拖期惩罚为目标，给出订单在工厂间最佳的指派方案和生产调度方案。

图1 分布式预制构件生产调度系统

1.1 相关假设与参数说明

对于该集成优化问题的相关假设有：1)所有机器在调度零时刻均为可用状态；2)不考虑机器故障、工件损坏等突发情况；3)订单在工序上处理完成之前不能被其他订单抢占；4)订单在相邻工序间的安装和运输时间忽略不计。

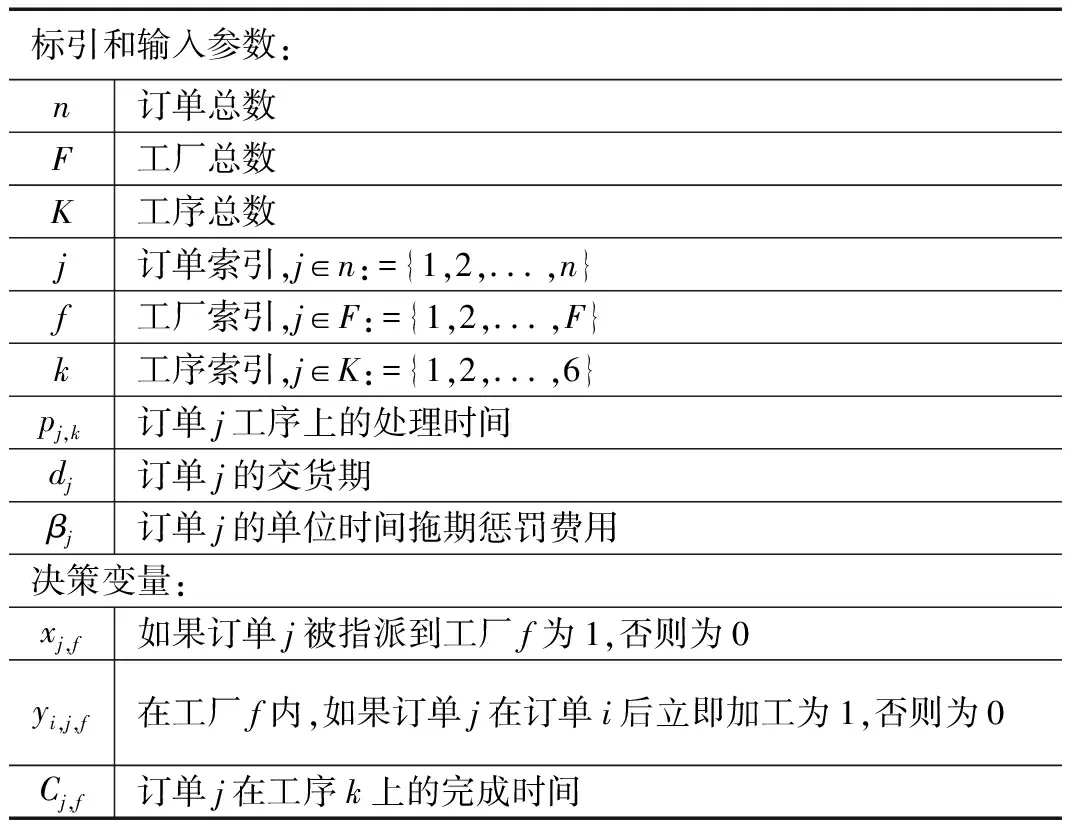
表1 调度模型参数说明

1.2 数学模型

基于以上符号和假设建立数学模型如下：

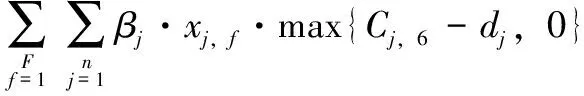
(1)

s.t.

(2)

(3)

(4)

Cj,k≥Cj-1,k+Pj,k,∀j,k∈K {4}

(5)

Cj,k≥Cj,k-1+Pj,k,∀j,k∈K {4}

(6)

Cj,k=Cj,k-1+Pj,k,∀j,k∈{4}

(7)

Cj,k≥0

(8)

式(1)为目标函数最小化订单总拖期惩罚费用；式(2)确保每个订单被指派到某一工厂中；式(3)和式(4)表示订单j是否和订单i指派到同一工厂，且订单j是否在订单i紧后加工；式(5)表示订单在工序上的处理时间不早于上一订单在此工序上的完工时间，第4道工序蒸汽养护为并行处理过程，不需满足此约束；式(6)表示订单在工序上的开始处理时间不早于该订单上一工序的完工时间；式(7)为并行工序完工时间的计算公式；式(8)定义了决策变量的取值范围。

2 离散教与学优化算法

TLBO算法原理[14]是模拟以班级为单位的学习方式，通过教师的“教”来引导班级学生成绩提高；同时，学生之间通过相互“学习”的方式进一步促进知识的吸收。其中，教师和学生相当于进化算法中的个体，而教师是对应目标值最佳的个体，学生成绩提高表示优化目标得到改进。TLBO算法算法分为3个阶段：1) 教师阶段：在班级中寻得最优解个体作为教师，引导班级中的学生搜索更好的解；2) 学生阶段：班级中学生通过与其他学生学习，获取比自身更好的解；3) 角色互换：在某次迭代中，若有学生寻得的解比教师的解更好，则在下一次迭代中将该学生替换为教师，教师降级为学生。

针对分布式预制构件流水车间调度该类非线性整数规划问题，本文在TLBO算法的基础上提出了一种离散教与学优化算法(DTLBO)，算法步骤如下：

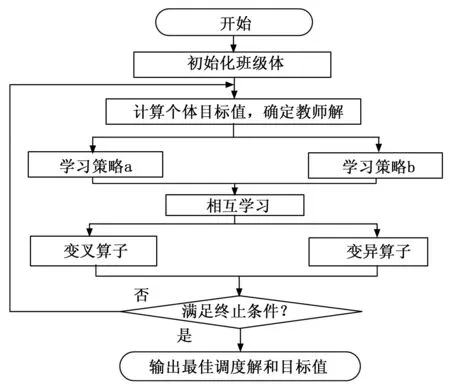
图2 DTLBO算法框图

Step1：通过结合启发式策略和随机生成的方式生成初始“班级”群体pop，确定教师解Xt；

Step3：学习阶段，学习阶段分为相互学习和自我学习，相互学习过程是随机将学生个体两两配对，进行与步骤2相同的信息交互操作，若得到的解质量更好则更新学生个体；

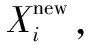
Step5：将学生个体Xi中目标值最优的个体X*取出与教师解Xt比较，如对应目标值更佳，则将X*替换为Xt；

Step6：判断是否满足终止条件：否，返回步骤2；是，输出最终教师解Xt和对应目标值。

2.1 调度解编码解码方式

以10订单和3预制构件工厂的问题为例，如图3所示，从区间[1,F]随机生成n个数字作为解的第一层，从区间[1,n]生成n个不重复的数字作为解的第二层。一层编号为 (1, 2, 1, 3, 2, 3, 1, 2, 3, 2)表示订单到工厂的指派方案，二层编号为 (8, 7, 3, 2, 5, 6, 10, 1, 9, 4)。即订单 (8, 3, 10) 被分配至工厂1处理；订单 (7, 5, 1, 4) 被分配至工厂2处理；订单 (2, 6, 9) 被分配至工厂3处理。订单在厂内的处理顺序如括号内从左到右所示，如此确定了订单在不同工厂间的指派方案以及生产调度方案。

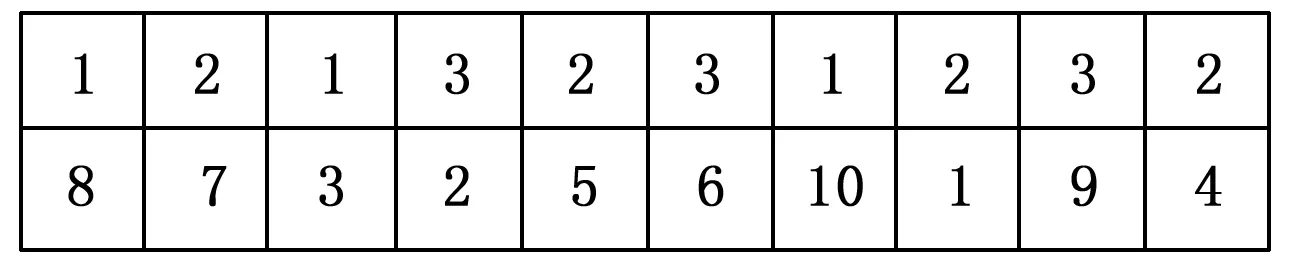
图3 编码示意图

2.2 初始化“班级”群体

为了避免随机方式产生的初始解群体质量较差，设计了一种启发式策略，即按各订单交货期排序，再将每个待加工订单依次分配至各工厂，基于该策略生成一个班级个体，其余班级个体通过随机方式生成。通过启发式规则和随机生成融合策略提升初始解的质量，来增加算法的寻优效率。

2.3 教学阶段

在教学阶段，结合问题模型双层编码结构的特点，设计了两种学习策略，通过让班级中每个学生个体随机选择两种学习策略中的一个与教师进行信息交互，提高班级学生的成绩。两种学习策略内容如下：

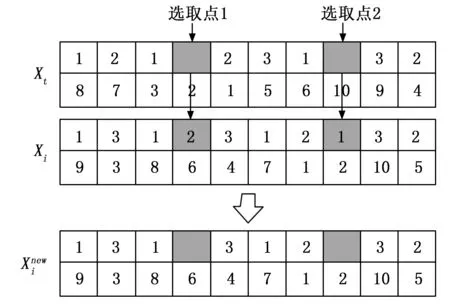
图4 顶层替换

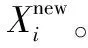
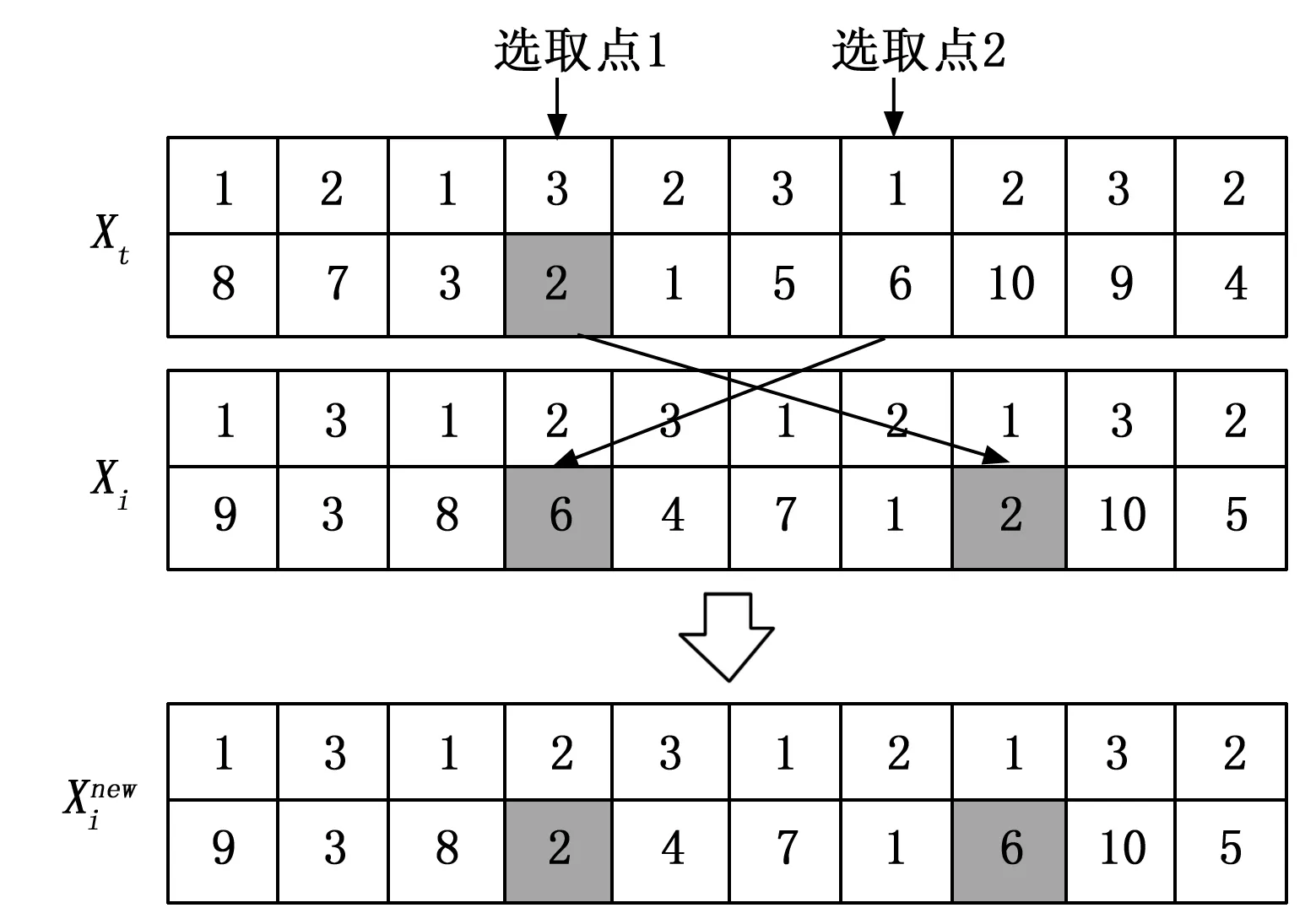
图5 底层替换

2.4 学生阶段

2.4.1 相互学习

将学生个体两两随机配对，进行与教学阶段相同的信息交互操作，若得到的解质量比相互学习前更好则更新学生个体。

2.4.2 自我学习

本文结合问题模型的特点，设计了两种自我学习过程：

1) 如图6所示，将每个学生个体Xi取出，通过变异算子在解的第一层随机选取两个位置点，然后从[1,F]内随机产生和选取点不一样的值进行替换，从而改变订单在工厂间的指派。

图6 变异算子

2) 如图7所示，将每个学生个体Xi取出，通过交叉算子在解中随机选取两个位置点，将两位置点一二层包含的元素整层互换，从而改变订单的生产调度排序。

图7 交叉算子

2.5 参数设置

为了评估DTLBO算法的性能，将其与生产调度领域常用的智能算法GA[19]和VNS[20]作对比。公平起见，3种算法的终止准则统一设置为最大运行时间t=n*6/10。需要调节的参数为DTLBO的种群大小 (pop)，以及GA算法的种群大小 (pop)、交叉率 (pc) 和变异率 (pm)。参数调整结果如下：

1) DTLBO：pop=100；

2) GA：pop=80，pc=0.9，pm=0.1。

3 分布式预制生产调度系统

3.1 系统原理

分布式预制生产调度系统的原理是：先将设定好的算法导入上位机，上位机接收到来自客户的订单信息，包括订单数量、构件类型、交货期以及各类型构件延期交付的惩罚费用；然后上位机根据订单信息计算出最佳的订单指派和调度方案；最后通过下位机将调度方案显示反馈给生产管理人员，管理人员依据给出的调度序列控制各预制构件订单的开工时间完成调度工作。

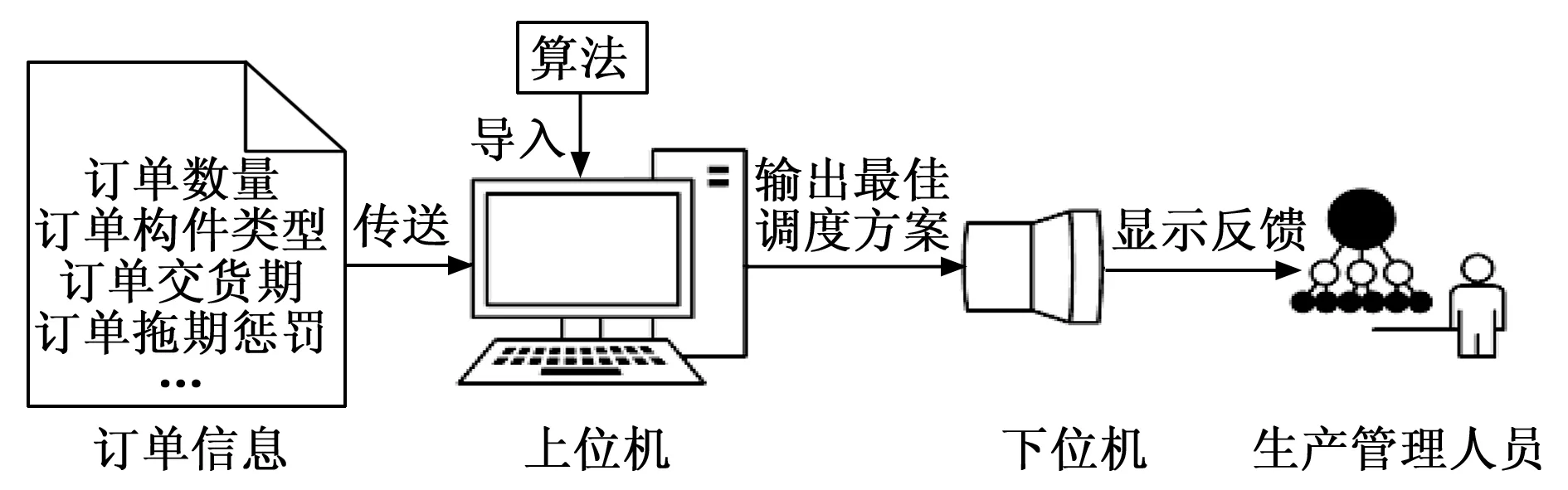
图8 系统原理图

3.2 调度过程

以2.1节给出的10订单调度解为例，首先对其进行解码，得出最终可指导实际生产的调度方案，如表2所示。

表2 调度方案

根据该调度方案将各订单依次指派到对应的工厂按序加工处理。以工厂1为例，首先在工序1上处理订单8，由式(5)～式(7)计算订单8在工序1上的完成时间，并作为其紧后处理的订单3在工序1上的开工时间，再通过式(5)～(7)计算订单3在工序1上的完成时间，依次类推计算得出预制工厂1内生产调度序列 (8 3 10) 内所有订单在1～6工序上的最佳开工时间、完工时间。生产管理者通过控制各订单的开工时间完成对订单的生产调度，并且已知各订单最终的完工时间和各订单的交货期，带入目标函数式(1)即可算出总订单拖期惩罚费用。图9为厂1内预制构件订单生产调度甘特图，该图反应了经算法优化后的各订单在每道工序上的最佳开工时间及完工时间。

图9 生产调度甘特图

4 仿真实验与结果分析

实验通过Matlab 2018b编程实现，计算机配置为Microsoft Windows 10，处理器为Intel Core i5-9400F CPU @ 2.9 GHz/8 GB RAM。通过不同规模下的算例实验，对各算法求解分布式预制构件调度问题时的鲁棒性和求解性能进行比较分析。

4.1 测试实例

如表3所示，每种类型订单各工序的处理时间取自Brandimarte等[21]文献中的标准数据，订单的单位时间拖期惩罚系数βi∈{10,20}，问题实例的交货日期di在区间[PT‘n,3*n]均匀分布生成，PT为所有订单处理时间的累加和。实验中设定预制构件工厂数量为3，考虑了20、30和50三种待调度订单数量，在每种数量规模下测试了5个问题实例，每个问题实例运行20次，记录20次运行取得目标值的最小值 (Min) 、平均值 (Avg)和标准差 (Std)。

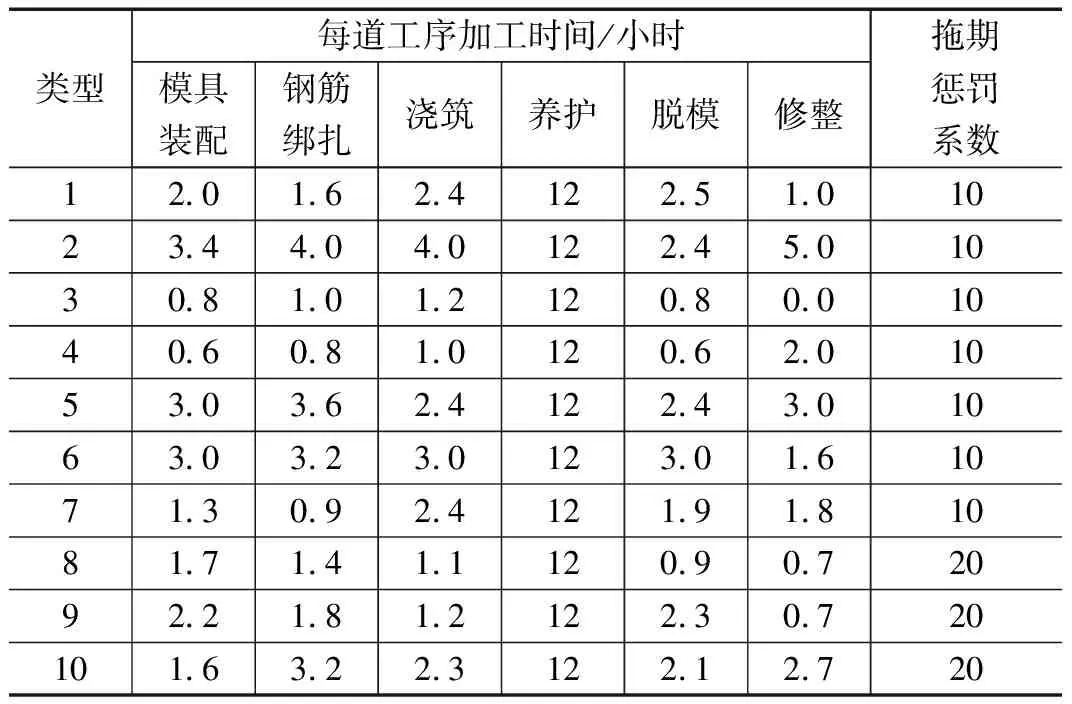
表3 订单生产信息

4.2 算法性能对比分析

为了直观地比较3种算法性能的优劣。本文采用相对偏差率(RPD，relative percentage deviation)来评估各算法的性能。计算公式如下：

(11)

(12)

4.3 实验结果分析

表4记录了各算法在计算20、30和50三种不同待调度订单数量问题实例下得出的最小RPD值、平均RPD值和Std值。为了便于区分，对同一个问题实例各算法得出的最小RPD值用粗体表示，最小平均RPD值用粗斜体表示，最小Std值用斜体表示。

从表4可以看出，实验测试了不同订单规模下的15个算例，对于各算例下的最佳平均RPD值和最小RPD值，均由DTLBO算法取得。各算例最小的Std值，DTLBO算法取得了14个。图10是3种算法在求解不同订单规模问题时的ARPD值对比图，可以看出在3种订单数量问题下，本文提出的DTLBO算法均取得了最佳ARPD值。即表明，与GA和VNS相比，提出的DTLBO算法具有更好的求解性能和鲁棒性。

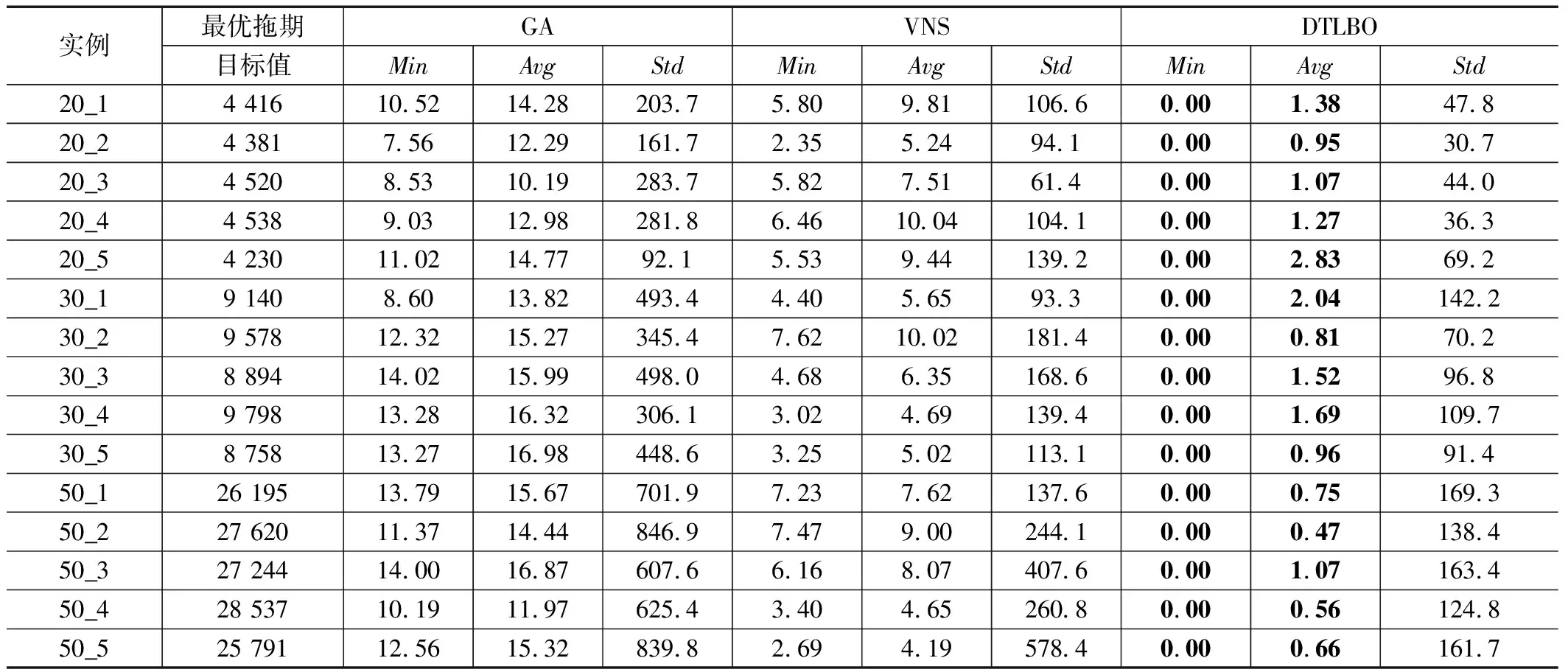
表4 实验测试结果对比

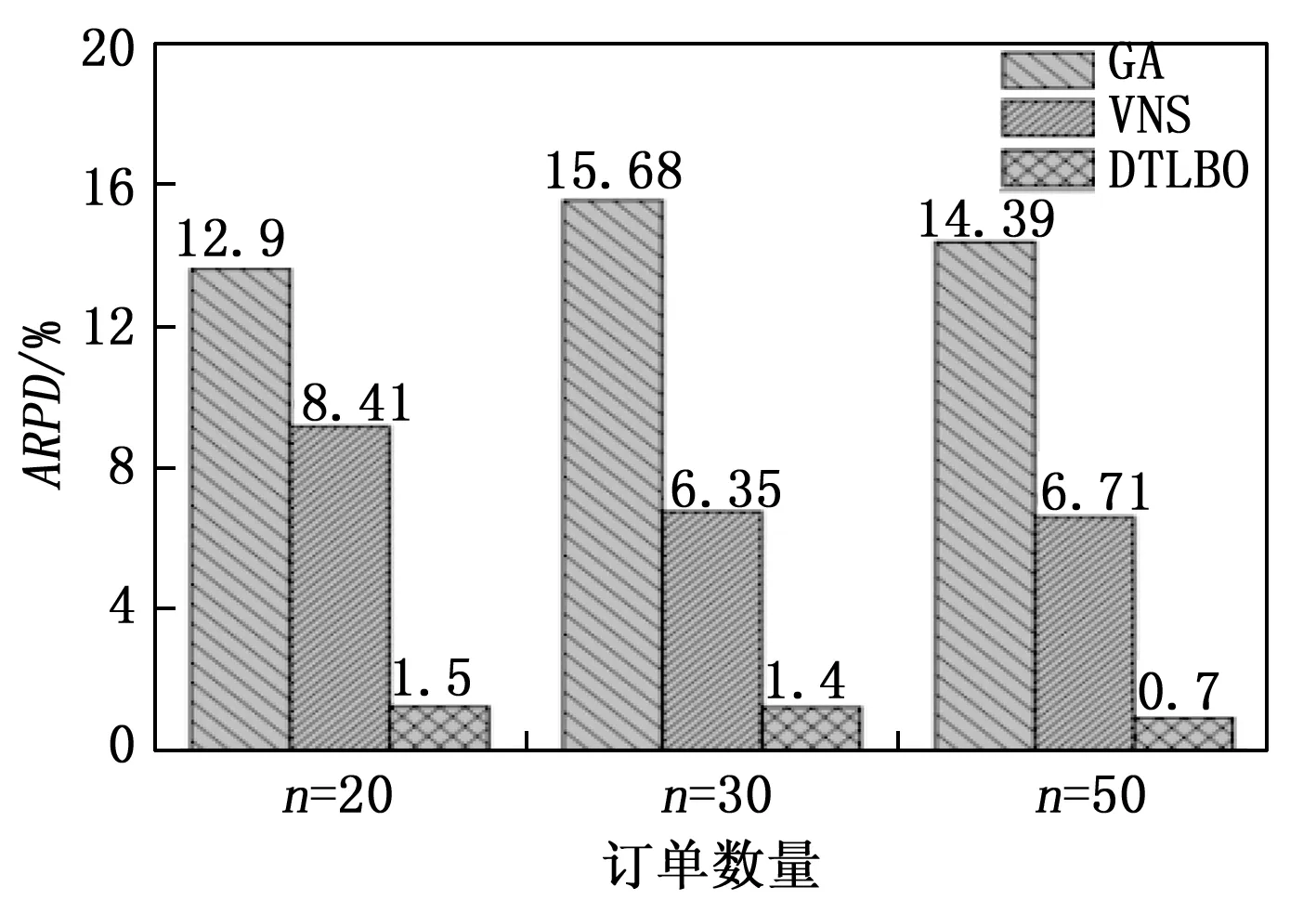
图10 各订单数量的平均偏差率图

以30订单规模下的算例5为例，图11为3种算法的迭代收敛曲线，可以看出DTLBO算法不仅有较好的求解质量，且收敛速度最快。

图11 收敛曲线

4.4 与启发式调度方法对比

传统预制构件企业通常采用基于经验的启发式调度方法：即先将订单按交货期的早晚排序，基于贪婪的思想将交货期早的订单置于调度序列的前部，先进行加工处理，如此依次将各个订单分配置所有工厂内，得出调度方案。

为了验证本文提出算法的实际应用价值，表5统计了3种订单规模下分别通过DTLBO算法和启发式调度方法计算得出的平均目标值，DTLBO算法较启发式调度方法在目标值上的改进率分别为11.2%、10.8%和12.4%。可以看出，使用DTLBO算法提供的调度方案可以为企业有效降低订单拖期惩罚费用成本，增加预制构件制造企业净收益。

表5 不同订单规模下DTLBO算法的改进率

5 结束语

本文针对分布式预制构件流水车间调度问题，以最小化订单总拖期惩罚为目标构建了非线性整数规划数学模型，并根据模型特点设计了双层整数编码形式，最后提出了一种离散教与学优化算法(DTLBO)应用于求解该问题。通过大量仿真实验，从最优RPD值、平均RPD值和Std值3个性能指标与VNS算法和GA算法对比分析，结果验证了提出的DTLBO算法在求解分布式预制构件流水车间调度问题时的有效性和可行性。在下一步研究中，可以将机器故障、临时订单等突发情形集成到调度问题中进行求解。