基于小波分解的多尺度PCA周期性攻击检测算法

刘学君，张小妮，栾海英，李凯丽，苏 鹏，黎 杨，晏 涌，沙 芸

(1.北京石油化工学院 信息工程学院，北京 102617； 2.北京机械工业自动化研究所有限公司，北京 100120)

0 引言

随着互联网技术和计算机信息技术的逐渐成熟、工业生产规模的逐渐扩大，把互联网技术应用在工业控制系统当中已经成为一种普遍现象[1]。近年来网络攻击手段越来越多样化也越来越隐蔽，出现的工业控制系统攻击事件不断增多，生产过程的异常或故障造成重大的经济损失、环境灾难甚至人员伤亡，促使国内外十分关注控制系统的信息安全[2]。不同于传统IT网络着重研究网络层内的数据安全，工控系统强调的是物理层的信息[3]。一旦业务数据被篡改，就会对整个工控系统工作状态出现误判，因此，对工控系统业务数据攻击进行研究，有利于提高工控系统的安全性。目前该领域的研究是基于工控系统上位机的历史数据，采用状态监控和异常检测算法进行研究，如Amin等人[4]对水利灌溉SCADA建立被控系统状态模型进行研究以及Teixeira等人[5]对电力控制系统的研究，但是他们的研究对于周期性的隐蔽攻击效果有待提高。周期性攻击[6-8]是注入一定幅值的周期性信号，幅值会长时间里在小范围内波动并且低于工控系统的报警线，直接从数据上无法分辨，报警器也不会提示，但是此时从设备采集的业务数据是异常的。针对此类工控业务层数据中周期性攻击，本文采用小波变换和多尺度主成分分析，把数据分解到多个尺度进行检测。

1 算法原理

1.1 小波变换

小波变换因其在时间-频率分析中所表现出的优越特性，被广泛应用在信号处理上。它继承和发展了短时傅里叶变换局部的思想，同时又克服了窗口大小不随频率变化等缺点，能够提供一个随频率改变的时频两域的窗口。小波变换能够充分突出某些方面的问题特征，能够对时间(空间)频率的局部化分析，通过伸缩平移运算对信号(函数)逐步进行多尺度细化，最终实现高频和低频处频率细分[9]。张涛等人[6]采用离散小波变换的方法对采集到的数据集进行分析。

小波变换将信号分解为逼近和细节两个过程[10]。信号f(t)小波离散变换[11]为:

(1)

式中，Φ(n)为小波函数，Φ*(n)为Φ(n)共轭，a为尺度参数，b为位移参数。本文把数据分解为两层，分解后的数据为三维数据，具体的分解如图1所示。

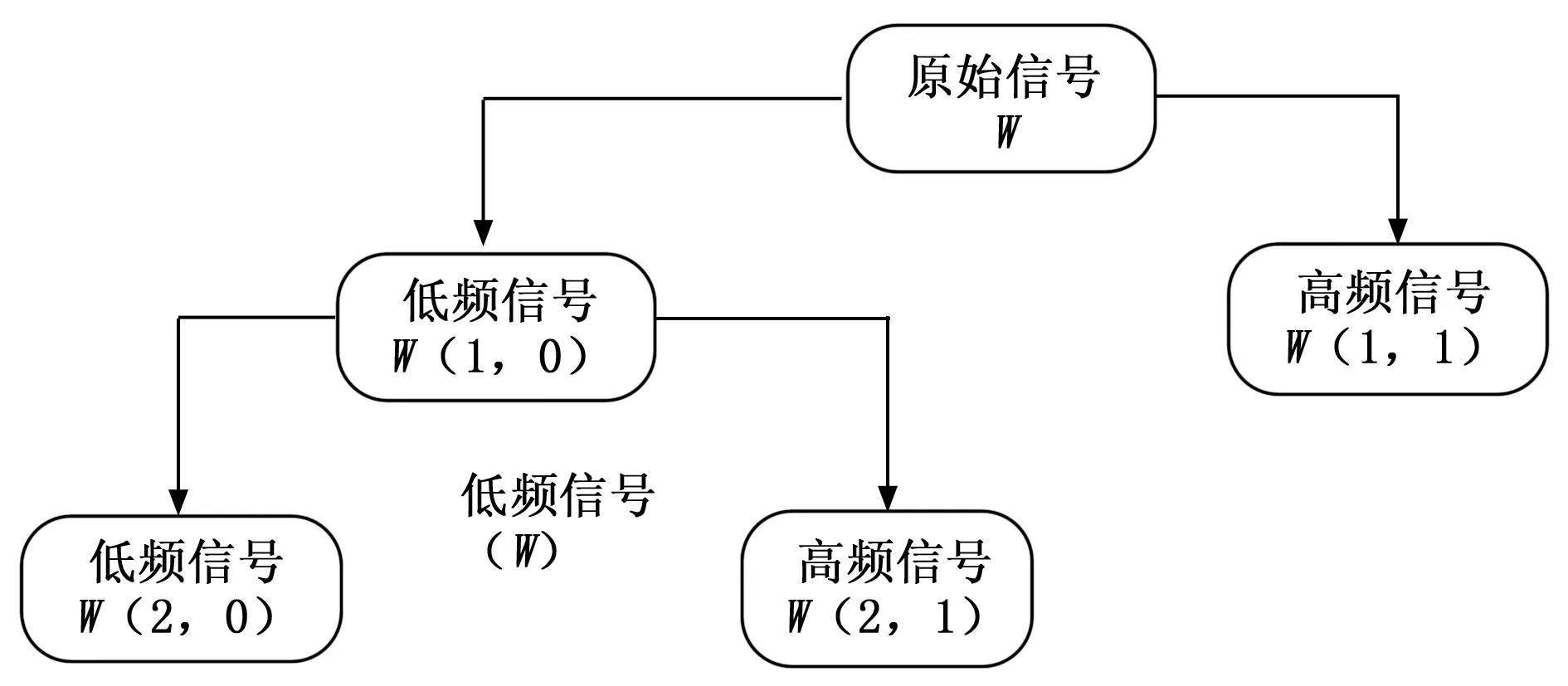
图1 小波分解示意图

1.2 多尺度主成分分析原理

利用小波分解把数据分为多个尺度每一个尺度作为一个训练集，对每一个训练集做主成分分析(PCA,principal component analysis)，根据累计贡献率确定主元个数以及协方差矩阵的特征值和特征向量，来建立单个尺度的PCA模型，把每个尺度包含重要信息的PCA模型整合成综合的PCA模型[12]。为提取单个模型的有效数据以及检测新数据是否受到攻击，引入了T2统计量和SPE统计量的控制限[13-14]确定单尺度的PCA模型。

T2统计量是表征PCA模型内部变化的一种预测，具体定义如下[15]：

(2)

其中：n为建模数据的样本个数，α为显著性水平，在自由度为n-k，k条件下F分布临界值。正常工控下，T2应该满足下式：

(3)

(4)

式中，k为主成分模型中保留的主成分个数，λa为建模数据X的协方差矩阵的第a个特征值。

SPE统计量是模型外部数据变化的一种测度，具体定义如下[16]：

(5)

(6)

(7)

其中：Ca为正太分布在显著水平a下的临界值，λj为X的协方差矩阵的特征值。正常工控下，SPE应满足下式：

SPE≥SPEa

(8)

SPEa是SPE统计量的控制限，可有下式计算得到：

(9)

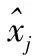
正常工控下，SPE和T2应同时满足：

(10)

若其中至少有一个不满足，则表明数据遭受攻击。

2 建模与测试

本文以工控网络数据集来研究周期性攻击检测的具体的建模过程。目前工控方面公开数据集中异常数据一般不含周期性攻击，所以本文构建了3种周期性攻击的模型。由于周期性攻击是在幅值和频率上做微小变化，更接近偏差攻击，因此3种攻击模型是在偏差攻击模型上进行修改。

假设所有数据Q集合数据遭受攻击，则偏差攻击模型定义如下[17]：

(11)

y(n)表示原始数据,幅值为E,在部分数据上加上一个小幅值构成偏差攻击。正弦攻击在偏差攻击的基础上添加频率特性攻击，使其隐蔽性更高。正弦攻击模型如下：

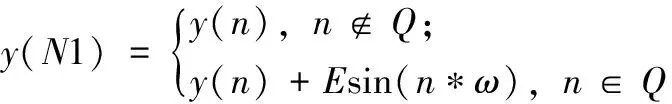
(12)

式中，正弦攻击角频率ω决定攻击信号周期，幅值E决定攻击强度。

假设方波攻击周期为N，幅值为E，把攻击加入集合Q。则方波攻击模型如下：

(13)

三角波攻击与正弦攻击类似，但是正弦攻击相较于三角波攻击更平缓。假设三角波攻击的周期为N，幅值为E，把攻击加入集合Q。三角波攻击模型如下：

(14)

式(11)是偏差攻击的模型，根据模型生成异常数据的方法是原始数据叠加一个相较于原始数据较小的数值。式(12)是正弦攻击模型，与偏差攻击模型的区别是叠加的幅值乘上了一个正弦函数，即原始数据叠加数据遵循正弦规律变化。式(13)是方波攻击模型、式(14)是三角波攻击模型，根据模型生成数据的方法与正弦攻击相同。

通过模型生成异常数据后，选取正常数据作为训练集，对选取的训练集做数据预处理，数据预处理包括去中心化和标准化。处理后的数据做小波尺度分解，如(1)式所示，把数据分为多个尺度，具体分解的层数根据实际情况而定。文采用的小波函数是Daubechies简称为dbN，其中N为小波的分解阶数。小波ψ(t)和尺度函数φ(t)中的支撑区为2N-1，ψ(t)的消失矩为N。本文用到的N=2，dbN没有明确的表达式，但转换函数h的平方模是明确的。

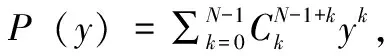
(15)

其中：

(16)

Daubechies小波函数提供了比Haar函数更具有效的分析和综合。

采用训练集训练综合模型，首先把正弦攻击、方波攻击和三角波攻击叠加正常数据作为测试集。其次把测试集进行尺度分解，在对应尺度上的PCA模型中进行测试。最后如果一个测试集在多个单尺度PCA模型当中都检测出了攻击，就采用综合尺度的PCA模型即多尺度主成分分析(MSPCA，multi-scale principal component analysis)进行检测，算法流程如图2所示。

图2 异常数据检测流程图

由图2可知，算法的运行步骤如下：

1)首先对训练集数据预处理，在预处理阶段是对数据进行标准化，采用小波滤除噪音，并分解为多个尺度。

2)其次在多个尺度的数据上分别训练单尺度的PCA模型，把各个尺度提取出来的重要信息组合成新的矩阵，求取新矩阵的两个控制限得到综合模型。

3)最后在测试集上进行测试，测试集数据进行预处理，然后输入到综合模型中，如果存在数据只要超出一个控制限，那么判定数据为异常数据并输出，反之为正常数据。直到把所有的数据检测完，算法结束。

3 实验结果与分析

3.1 实验步骤

3.1.1 构建数据集

把原始数据集按照9∶1的比例划分为训练集和测试集。使用公式(12)～(14)模型构建异常数据，幅值设为原始数据集的数值的1%～2%，频率设为100～1 000之间。根据3个模型随机产生3组数据。3组随机数分别随机叠加到部分测试集上，形成3组含有异常数据的测试集。

3.1.2 训练模型并进行检测

把训练集输入到算法经训练得到综合模型，对测试集进行检测。测试过程中为便于观察实验结果，在算法之中加入显示模块和数据统计模块。显示模块画出各个数据与综合模型两个控制限的距离，并把两个控制限显示在两幅图中，只要超出一个控制限，数据就为异常数据。数据统计模块将会输出异常数据的位置以及异常数据的数目。

3.2 实验方法

本文采用同一训练集分别训练综合模型和PCA模型，然后分别统计综合模型和原始PCA算法检测出的异常数据数目，来比较两个算法检测效果。

3.3 实验结果

本文采用两个数据集进行实验，并用python中matplotlib进行绘图。每组实验结果两张图，T2统计量图和SPE统计量图，图横轴表示样本，纵轴表示统计量值。两张图中的横线表示综合模型的控制限。

3.3.1 密西西比数据集

密西西比州立大学基础设施保护中心于2014年建立的工控入侵检测数据集，数据源为天然气管道SCADA控制系统网络层数据，包含4种类别的攻击，26个特征和1个标签值[18-21]。

1)三角波攻击测试集实验结果：

图3和图4分是PCA和MSPCA对三角波攻击的检测结果，三角波的攻击幅度是正常数据±2%。左右两幅图的横线以下为正常数据，超出其中一条都为异常数据。由图3和图4对比可见，图4中检测出的异常数据更多，对数据分解以后再检测的灵敏度要高于原始直接检测的灵敏度。

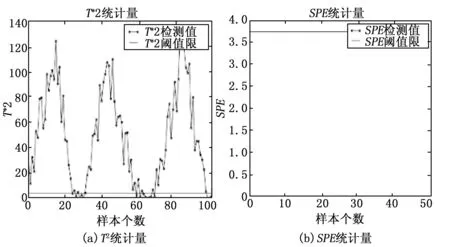
图3 PCA检测三角波攻击的结果

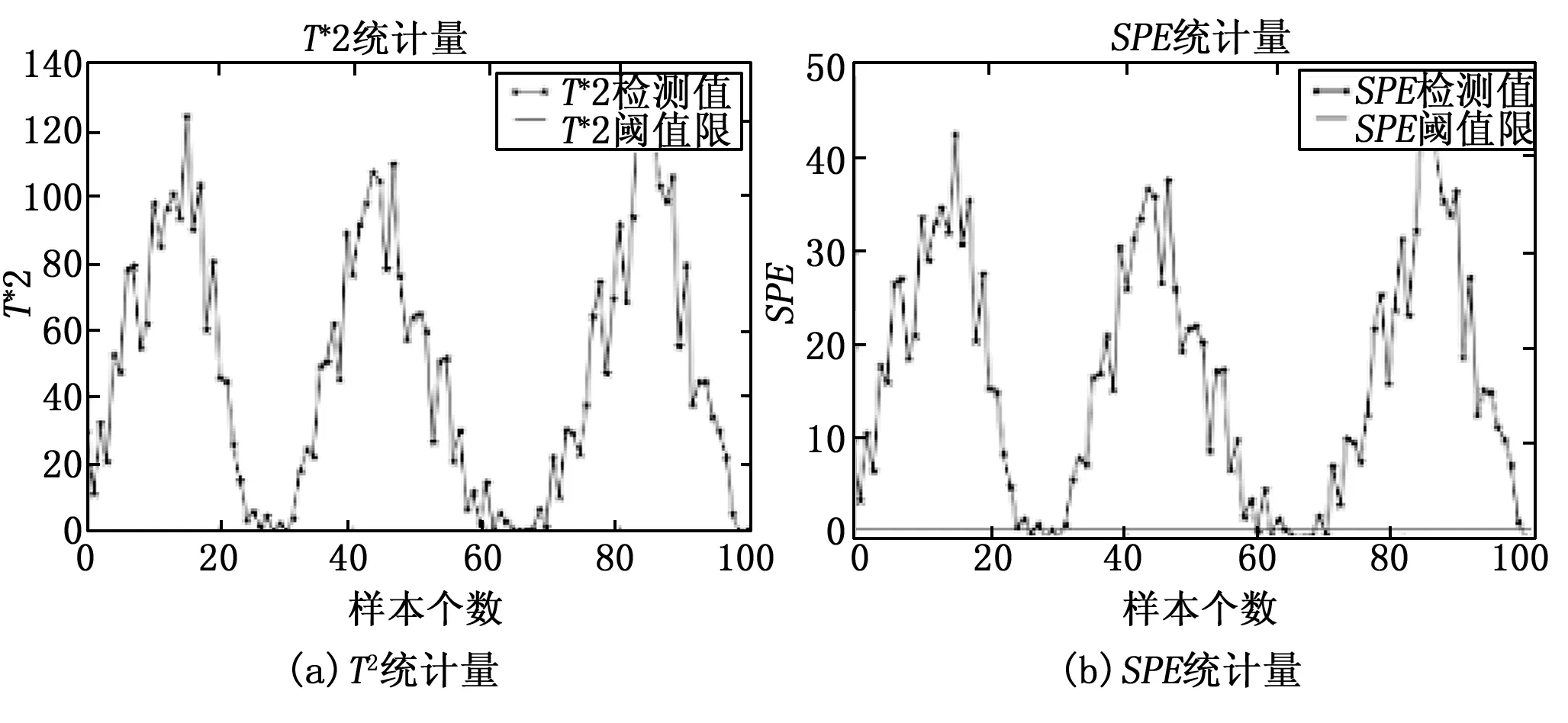
图4 MSPCA检测三角波攻击的结果

2)方波攻击测试集实验结果如图5和图6所示。

图5 PCA检测方波攻击的结果

图6 MSPCA检测方波攻击的结果

图5和图6分别用PCA和MSPCA对方波攻击的检测结果，攻击幅度是正常数据±2%。由两组对比结果可知图6中数据分解后检测出来的异常点较多。

3)加入正弦攻击，检测结果如图7和图8所示。

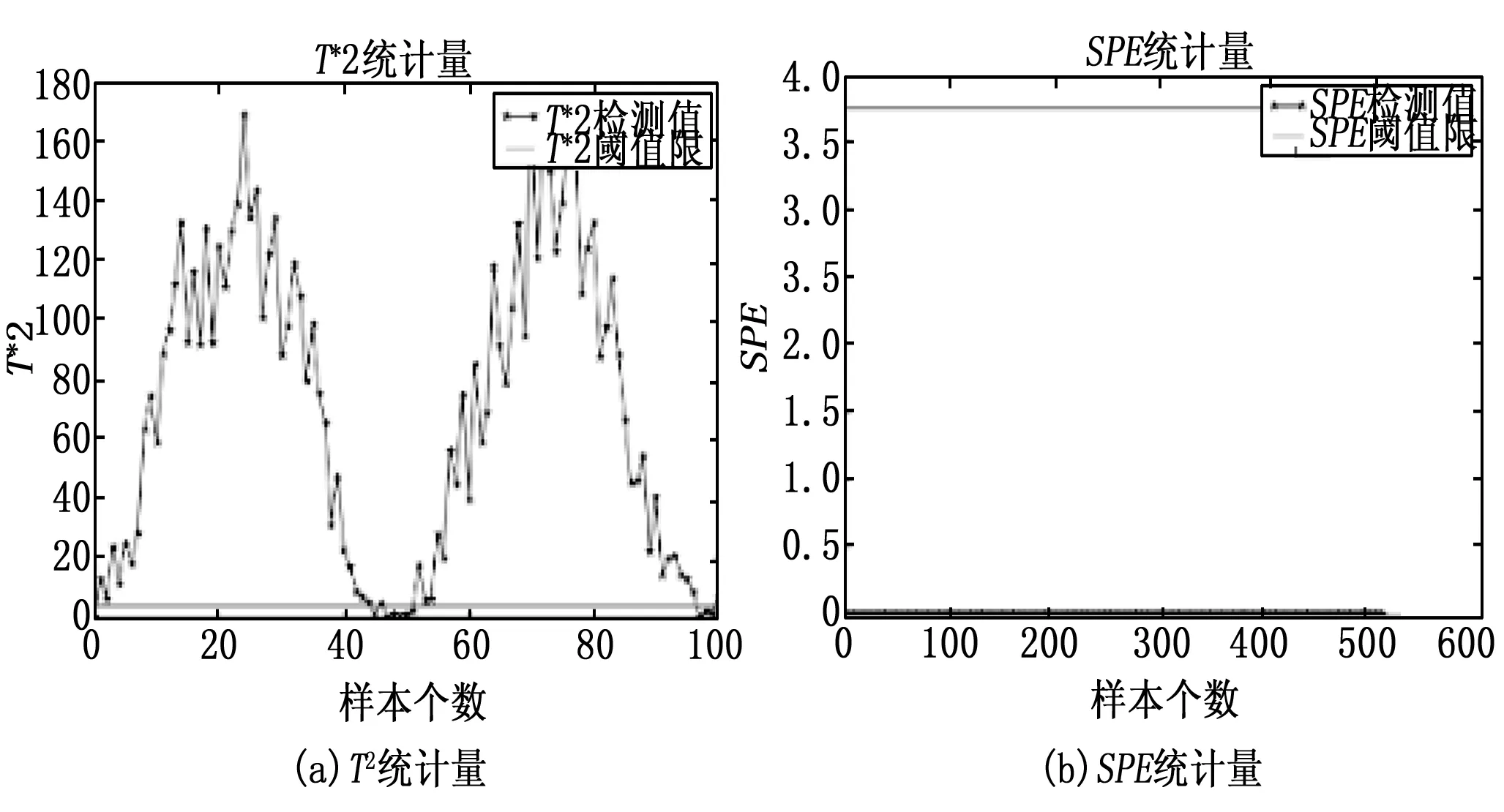
图7 PCA检测正弦波攻击的结果

图8 MSPCA检测正弦波攻击的结果

图7和图8为正弦攻击检测结果，攻击幅度是原始数据的1%，在单尺度检测中仅依靠T2统计，而在MSPCA模型当中，是由T2统计和SPE统计检测共同决定。由图像可知图8中MSPCA检测出来的异常数据要多于PCA检测出来的数目。

3.3.2 自建数据集实验结果

自建数据集是对某工控系统的多个设备采集数据，其中包括油罐的液位、压力以及温度、管线压力等共包含131个特征和1个标签。

图9和图10为某工控系统数据叠加正弦攻击后采用算法检测出来的异常数据，其中攻击幅度为攻击前幅度±1%。

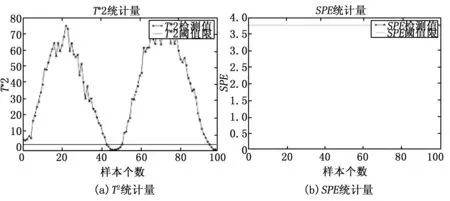
图9 PCA检测正弦波攻击的结果

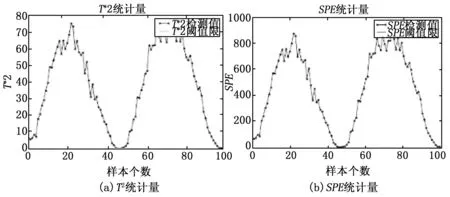
图10 MSPCA检测正弦波攻击的结果

由图9和图10 的检测结果可知，在攻击幅度极小的情况下，图10中MSPCA检测效果依然比图9中PCA异常检测效果好。

3.4 实验分析

工控系统为了保证数据的时效性，数据集采集的频率比较高，系统设备传感器数据变化量比较小，所以各个攻击类型的攻击幅度比较小控制在1%～2%之间。通过3.3节两个数据集上的几组实验结果图可知，MSPACA的检测效果要高于PCA算法，具体的实验统计数据如表1所示。

表1 正弦攻击检测统计

由表1可知，多尺度的主成分分析在多种类型的攻击的检测结果均优于传统的主成分分析算法，适用于检测相关工控系统业务数据的异常。

4 结束语

针对工业控制系统采集到的各设备运行数据的周期攻击，本文首先采用小波变换进行尺度分解，然后再对每一个尺度做主成分分析记录每个尺度的PCA模型，通过指标来筛选出每个尺度有价值的数据，去除冗余，构成MSPCA模型,对隐蔽性比较强的周期性攻击提高了检测效果。同时，根据输出的异常数据可以确定受攻击的时间和所攻击的位置。下一步可以围绕提高MSPCA的准确率和灵敏程度做进一步研究和探索。