在小学低年级计算教学中如何培养学生的知识迁移能力
魏彤
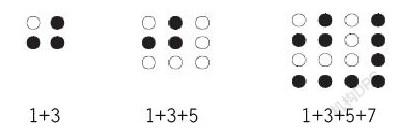
【摘 要】小学低年级阶段的学习是整个学习体系的基础,而计算教学在小学数学教学中至关重要。计算教学的主要作用在于培养学生的计算思维和运算能力,因此,在计算教学过程中,教师不仅要注重学生对计算方法的掌握,还要注重学生将数学知识应用于实际问题的能力的培养,即培养学生的知识迁移能力。迁移作为培养学生的数学能力以及问题解决能力的有效突破口,教师应该尤为注意迁移教学的高效性,要培养学生举一反三的能力,提升自身的数学素养。本文从低年级实际情况出发,浅析在小学低年级计算教学中该如何培养学生的知识迁移能力。
【关键词】小学低年级;计算;知识迁移
学校教育对于人的发展尤为重要,而学校教育的核心就是要让学生能够以旧带新,掌握好的学习方法,做到知识的迁移,而并非灌输课本知识。而对于低年级的小学生而言,他们的数学知识储备比较少,数学思维能力有待完善和提升,但是求知欲和好奇心都比较旺盛。所以,在这个阶段,教师要能够提供足够的指导,帮助学生由抽象联系实际,从而逐渐培养知识迁移能力。那么,在小学低年级的计算教学中,作为教师该如何更好培养学生的知识迁移能力呢?
一、加强学科知识的理解,夯实迁移基础
全面深刻地理解、概括数学课程的一般原则是实现知识迁移的一条非常重要的途径。因此,在数学课堂教学时,要积极引导学生运用原有的知识经验去理解新学习的内容。在这一学习过程中,教师应该提前了解学生情况,判断学生是否满足要求,倘若不能,也就是当学生出现已有的储备知识对于新知识的理解有困难的情况时,教师就要及时的给学生补充必要的知识,为以后学习打下基础,也为知识迁移打好基础。
例如在教学一年级的加减法之前,学生必须对于前面的《分与合》的内容有了较为深刻的记忆和理解,才能以这些知识为基础,迁移到10以内的加减法的学习,如果学生对于《分与合》的内容不理解也没有记忆,那么他们将会对这一部分乃至后面20以内的加减法以及100以内的加减法的计算学习感到非常吃力。
二、创设新旧知识联系的情景,搭建迁移桥梁
知识迁移的根本是原有知识。因此,原有的知识是坚实的基础。因此,有效的知识迁移需要新旧知识的联系,这就要求在课堂教学中,教师不仅要重视向学生传授知识,还要能够引导学生联系已经掌握的知识。因此,教师可以设置情景来联系新旧知识,从而搭建迁移桥梁,实现知识的迁移。
例如在教学一年级20以内的加减法中的《8、7加几》这一课的内容时,由于在前一课时学生已经有了计算9加几的计算经验了,而这两节课中涉及到的计算方法和计算原理是相似的,因此教师可以在教学时先出示几道9加几的算式让学生计算并且让学生说说计算的过程,同时在探究8加几计算方法的过程中引导学生用学过的方法试着算一算,从而实现知识迁移。
三、强化直观抽象教学间的联系,促进知识的迁移
数学学科具有抽象性,从而良好的抽象概括能力,对于学生学好数学学科尤为重要,同时也有助于提高学生知识迁移能力。如果学生概括事物的能力很强,那他们对于知识的迁移能更有效地切入,从而更好地掌握新知识。因为进行抽象概括的基础是具有较强的感性认识,所以教师在引导学生进行抽象概括时,应该鼓励学生对于具体形象的事物尽可能多的积累,从而提升感性方面的认识。在教学时,教师应充分利用具体的教具,学生充分利用具体的学具,使得学生感受直观与抽象间的联系。
我们知道,计算教学中最常用的教具就是小棒和计数器了,而低年级的孩子对于抽象的数学知识理解起来更是有困难,因此在实际教学时,要让学生能自己动手来实践体会。例如在教学二年级认识万以内的数这一部分内容时,其中关于数的组成这一课时,是完全建立在认识小棒和计数器的基础之上的。只有当学生掌握了一小捆小棒是“十”,一大捆小棒是“一百”,以及关于计数器中的相关知识之后,才能进行这一部分的学习。还有在教学一年级的分与合,在课上,也是要依靠小棒去进行探究各个数的分成与合成,倘若完全靠学生在头脑中想象每个数的分与合,教学效果肯定大打折扣,毕竟低年级的孩子比较小,他们是理解不了的。
四、注意科学合理的练习,在举一反三中促进迁移
能够突破教学中的重难点是教师在所有教学活动中的主要任务和障碍。正所谓要究其根本、对症下药。因此要突破课上的重难点,首先一定要明确教学中的“重”和“难”分别在哪里,接着要运用合理、正确的教学策略,最后要落实精讲精练的原则,让学生能自主联系新旧知识。在课上,教师应注重设计科学合理的练习,只有设计出具有针对性、阶梯性和启发性的练习,才能让学生充分利用迁移规律去解决实际问题,同时也为后继学习的进一步迁移做准备。
例如:规律计算题(如下图)根据图中的规律以及下面的算式,完成第四幅图且写出对应的算式。
根据图可以看出图形的规律:在前一幅图的基础上又增加了一圈小圆圈,每次增加的个数都是比前一圈的小圆圈个数多两个,而小圆圈有实心的有空心的,第一圈空心,第二圈实心,第三圈空心……以此类推,而算式就是根据对应图形的规律算出一共有多少个小圆圈。从这一题中可以看到,在数学教学中,很多的知识都是相通的,数字计算可以用生动的图形来表现,而图形也可以用准确的数字来体现。学生在这一题中体会到了数字和图形之间的联系,当遇到类似的问题也会想到这种方法。
五、调整知识间的同化,避免形成负迁移
在教学中,当旧的学习经验影响到新学的知识时,称为负迁移。正迁移一般是建立在深入研究的基础上,而负迁移一般是对于知识的理解停留在表面,没有真正的理解。产生负迁移的前提一般是概念之间的共同因素,由于学生处在低年级阶段,他们往往对于相关概念的本质区别不易察觉,因此教师应该在教学中对于容易混淆的概念进行辨析对比,讲清内涵,揭示特征,避免负迁移的产生。
例如教学文字计算题:2个4相加的和是多少?以及2个4相乘的积是多少?学生在解决这两个问题时特别容易出错。这两个题目乍一看差不多,都是2个4,但是它们的本质是不同的。2个4相加可以列成算式4加4,也可以根据乘法含义列成算式2乘4,但是2个4相乘则只能列成算式4乘4。大多数学生对于这两道题出错的原因在于看到了“2个4”,第一反应就是根据“求几个几是多少用乘法计算”列出算式2乘4,并没有深入思考,就产生了负迁移。对于这两个题目,教师一定要让学生理解清楚题目的意思,明确题意之后再进行解答。
总之,提高学生的数学思维能力是数学教学的重中之重,而迁移能力又是数学思维的重要部分,因此在今后的数学教学中,广大数学教师还应继续努力,为创造出培养学生知识迁移能力的更多、更好的策略而做出自己应有的贡献。
【参考文献】
[1]王宗梅.迁移规律,让儿童的数学思维能力逐步提升[J].黑河教育,2018.
[2]孙孝忠.对当前小学数学课堂教学中一些现象的理性思考[J].江苏教育(小學版),2009.12
[3]王志民.连接生活素材感悟数学魅力[J].教学与管理(小学版),2009.1

