小净距隧道锚开挖参数优化分析*

邹典宽 李耘宇 彭瀚贤 吴雁杰

(1.武汉蔡甸经济开发区投资集团有限公司 武汉 430100；2.武汉理工大学交通与物流工程学院 武汉 430063； 3.广州地铁集团有限公司 广州 510220)

邻近隧道施工时，对既有隧道和围岩结构的影响较为复杂，需要监测隧道施工是否对既有隧道结构造成破坏，以及其施工扰动是否对围岩结构造成影响[1]。小净距隧道的施工难点在于中隔岩柱受力状态复杂、难以控制其稳定性[2]。合理的净距是确保中隔岩柱稳定性的关键，因此，许多学者都对小净距隧道的开挖参数进行了研究，张桂生等[3]提出以隧道中岩墙应力突变时的净距作为隧道合理净距的相关理论；王更峰等[4]通过计算分析魁岐双线八车道小净距隧道在采取不同开挖方式和不同净距情况下的相关参数，得出V级围岩条件下的合理净距为0.55B(B为隧道宽度，下同)；汤劲松等[5]通过对IV级围岩地层中茅山东隧道进行数值模拟，提出将塑性区的分布作为合理净距判断的指标之一；张永兴等[6]利用强度折减法，提出将安全系数突变时的净距作为合理净距；龚建武等[7-8]计算了浅埋小净距隧道的围岩压力特征，得出当隧道净距小于0.5B时，内侧围岩压力强烈受到净距影响的结论。

本文结合实际工程，通过分析掌子面错距，开挖台阶长度对隧道开挖过程中中夹土柱力学特征、围岩塑性区塑性区、地表沉降等参数的影响进行相关分析，以期得出能够有效限制锚洞附近地层沉降、降低围岩应力值、减小中夹土柱区域受扰动程度的较为合理参数取值。为更好地掌握小净距隧道锚洞周围应力分布情况，并及时有效地对相对薄弱区域设置支护，提供相应的技术参考。

1 工程概况

本文以宜昌市伍家岗长江大桥主桥北侧隧道式锚碇结构为研究对象，该桥位于湖北省宜昌市，南起点军区江城大道，北连伍家岗区花溪路。伍家岗长江大桥隧道锚结构见图1。

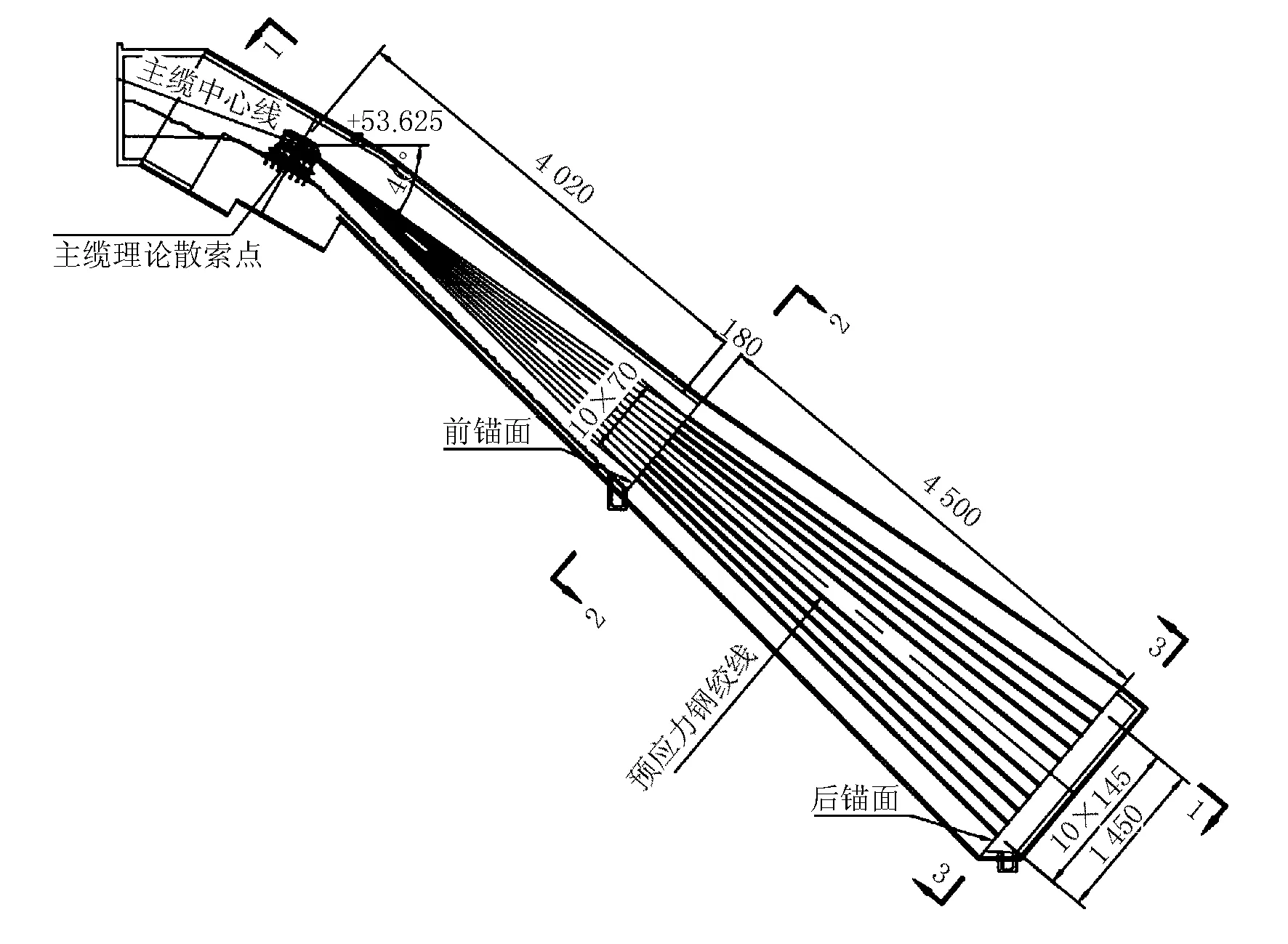
图1 隧道锚结构图

隧道式锚碇结构位于长江北岸低丘山体内，与最近公路相距40 m，与长江相距约480 m。主锚塞体呈前小后大的楔形状，轴线倾角为40°。隧道锚双洞中心距离37.50 m，最小净距约21.50 m，结合小净距隧道锚洞室变截面、大倾角的特点，实际工程中选择台阶法进行开挖，其中，前锚室段断面较小、围岩条件较好，采用两台阶法开挖，其余部分采用三台阶法开挖。

2 建立模型

2.1 计算模型

利用FLAC3D软件进行建模，充分考虑到开挖对周围土体扰动的影响，选取模型计算范围为150 m×140 m×60 m。隧道锚模型示意图见图2、图3。

图2 数值模型示意图 图3 隧道锚模型示意图

模型共有343 387个单元，189 267个结点。设置外部网格尺寸为1.2～6 m；精细化处理隧道锚处网格，尺寸取1～1.2m，并选取摩尔-库仑屈服准则作为岩体的本构关系模型。

对于边界条件，考虑三维模型地表面自由，底面及四周仅施加法向约束，由于隧道锚大部分属于浅埋锚洞，因此可以不考虑构造应力带来的影响，仅计算初始地应力。

2.2 围岩及支护计算参数

隧道锚洞口处岩体质量较差，存在强风化区，为V级围岩。锚塞体段岩体大部分为IV级围岩，少部分为III级围岩，相较于V级围岩稳定性较高且适合锚洞洞室开挖。根据地质勘察报告及工程实践经验，确定锚洞围岩力学参数见表1。

为了较为准确地控制隧洞开挖之后的围岩变形速率与变形值，在架设锚杆之外，采取架设工字钢钢拱架、铺装钢筋网、喷射C30混凝土的方式进行初期加固。由于超前支护在效果上相当于提升了围岩稳定性，在本文建立的计算模型中，将大管棚与注浆锚杆的超前支护作用列入考虑，围岩参数超前支护范围内得到相应提高，围岩力学参数见表1。

表1 围岩力学参数

同时，为了使计算更加贴近工程实际，依据等效原则并利用式(1)对钢拱架和钢筋网的支护作用的弹性模量进行换算，且将换算后的模量添加到喷射混凝土中。

式中：E为钢拱架换算后的弹性模量；Sg为钢拱架的截面积；Eg为钢拱架换算前的弹性模量；Sc为喷射混凝土的截面积。

3 掌子面错距对锚洞力学特性的影响

3.1 中夹土柱力学特性的影响

本次选取3个测点，在接近先行洞一侧设置测点1，在接近后行洞一侧设置测点2，选取测点3设置于测点1、2中心处。4.8 m错距下中夹土柱特征点沉降值沿纵向的变化曲线见图4，测点1、2、3对应的沉降曲线变化趋势基本相同，均呈现出先增加再降低最后增加并趋于稳定的趋势。

图4 4.8 m错距下中夹土柱特征点沉降值沿纵向变化曲线图

再对比相同纵深位置沉降值，可以看到1号测点为三者中的最大值最高可达3.11 mm，而3号测点沉降值则最小仅为0.91 mm。其原因为当先后导洞进行开挖后，锚洞临空面一侧受到围岩应力，同时，中夹土柱区域也受到传递而来的围岩应力作用。而左右导洞传递的围岩应力在中夹土柱区方向相反，导致3号测点处部分变形被抵消，这也是3号测点沉降值均小于1 mm的原因。并且，由图4中可知不同测点的沉降值在距后行洞掌子面约10 m处迅速减小，均在掌子面前方约6 m处趋于稳定。

针对测点1，从位移响应的角度分析，将掌子面错距分为0，2.4，4.8，7.2，9.6共5组，以距洞口纵向距离为变量研究测点1沿纵向沉降值的变化规律，不同错距下测点1沉降值沿纵向变化曲线图见图5。

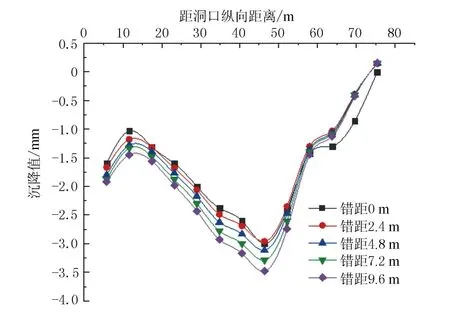
图5 不同错距下测点1沉降值沿纵向变化曲线图

由图5可见，1号测点的位移响应最明显，是中夹土柱沉降状况最具代表性的测点。在错距不同的情况下，测点1沿纵向沉降曲线变化趋势完全一致。当错距逐渐增大，沉降值的变化幅值不超过5.8%。随着距洞口纵向距离不断增加，除了错距为0 m之外，在距洞口纵向距离大于50 m处测点1的沉降值几乎不产生变化，这一现象也反映出掌子面错距的变化对于纵深方向测点1沉降值几乎不造成影响。

当错距为4.8 m时，中夹土柱特征点Y向位移沿纵向变化曲线见图6。

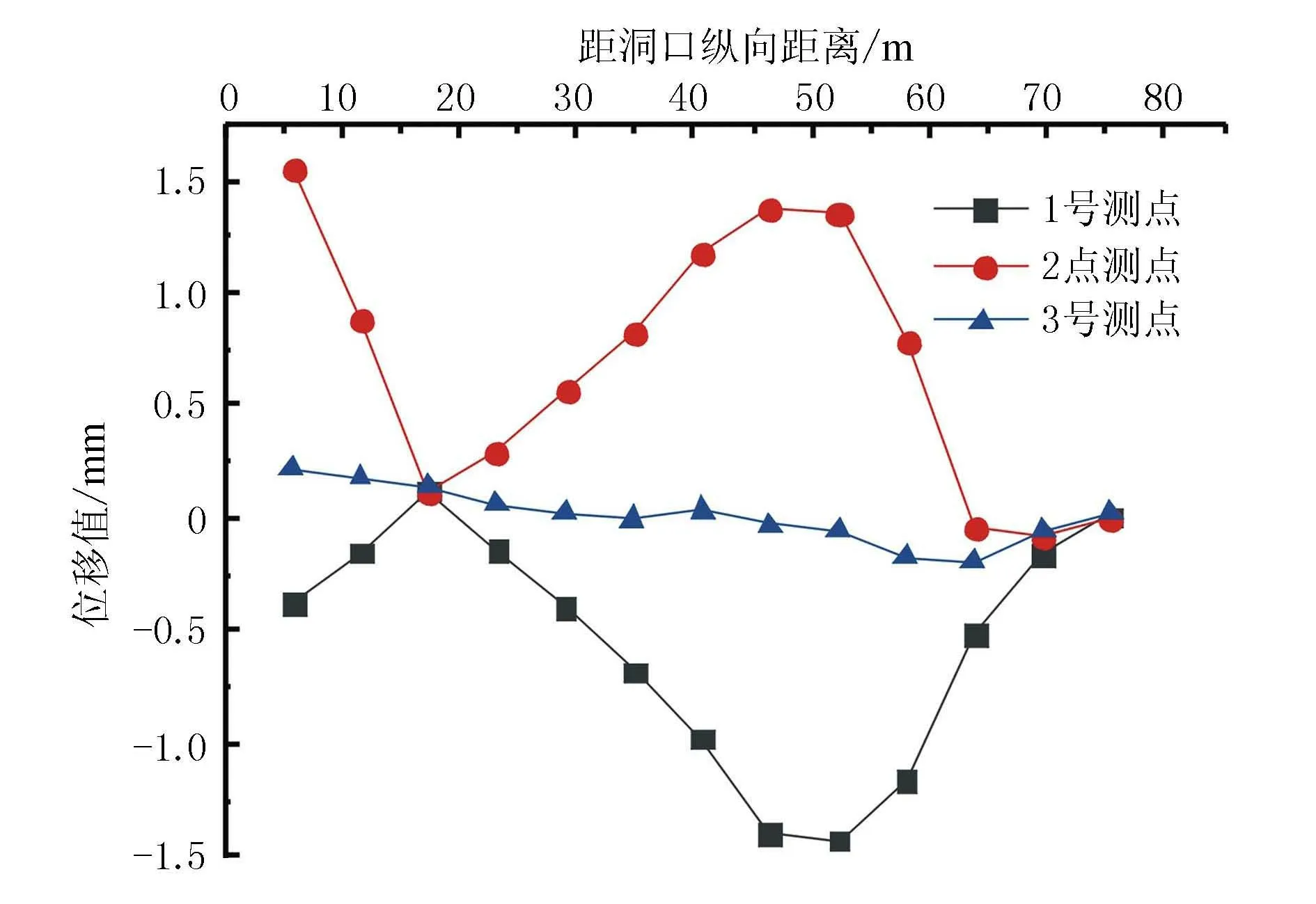
图6 4.8 m错距下中夹土柱特征点Y向位移沿纵向变化曲线图

由图6可见，锚洞开挖后，靠近先行洞的1号测点，附近中夹土柱偏移方向向先行洞一侧(即Y轴负方向)。而靠近后行洞2号测点，附近中夹土柱偏移方向向后行洞一侧。处在中夹土柱中心位置的3号测点，其横向位移在-0.19 mm与0.22 mm之间上下浮动，几乎可以忽略。由此可见中夹土柱区几乎不受锚洞开挖的影响。

不同错距下2号测点Y向位移沿纵向变化曲线图见图7。

图7 不同错距下2号测点Y向位移沿纵向变化曲线图

由图7可见，测点1、2的变化曲线沿X轴呈近似对称分布，且位移值均表现出“减小→增大→再减小”的变化趋势。且对比端点位移值，左端点处2号测点位移幅值超过1号测点约1 mm，且据洞口纵向距离超过70 m后三者位移值接近统一，可知后行洞洞口位移值大于先行洞洞口处，这是由于软弱土层对其影响较大。

由图7可得，5种错距取值对Y向位移沿纵向的位移值仅产生极小影响，除错距为0 m之外，曲线变化趋势大致相同甚至部分重叠。为减小横向位移，选取2.4 m或4.8 m错距作为合理掌子面施工错距较为合理。

不同工况下特征点处沉降值及其变化值具体参数见表2。

表2 不同错距下中夹土柱特征点降值对比

由表2可见，错距不同情况下，中心线位置的土体沉降值变化率最低仅为1.6%，最高则不超过3.3%，基本处于稳定状态。相较而言，靠近锚洞处，距中心线11 m位置土体沉降值较明显，其变化幅值也相对更大，最高可达0.19 mm，可以从中看出中夹土柱区靠近锚洞一侧在施工扰动的影响下沉降值大于中心线位置。

不同错距下中夹土柱沉降值变化曲线见图8。

图8 不同错距下中夹土柱沉降值变化曲线图

由图8可见，先行洞内侧土体沉降值相较于后行洞内侧高出约1 mm，且沉降曲线向先行洞内侧发生偏移。当掌子面错距不断增大时，中夹土柱区域的沉降值仅发生轻微的改变。如在距离中心线-11 m处，当错距为0 m时，沉降值为3.68 mm；当错距为9.6 m时，沉降值为4.29 mm，增幅仅为16.5%。综合以上变化参数可知，对于中夹土柱区域的沉降而言，掌子面错距的影响并不显著。

3.2 塑性区发展的影响

利用数值软件分析掌子面错距为0，2.4，4.8，7.2，9.6 m时塑性区发展情况，整理其结果见表3，另选取掌子面错距为2.4和4.8 m时隧道锚塑性区分布情况见图9。

表3 塑性区体积计算结果

图9 隧道锚塑性区分布图

由表3与图9可知，选取不同错距情况下，隧道锚中塑性区的分布基本一致，主要集中在锚塞体后半部分，而右侧塑性区分布区域相对较大是因为受到施工的二次扰动影响。锚塞体部分地层分界线处发生较大范围剪切破坏，应注意保持这一区域的锚洞围岩稳定性，及时施作支护结构。总体而言，错距不同对隧道锚塑性区体积影响可不予考虑，且不同错距对应的塑性区体积之间没有明显联系或差别。

4 台阶长度对锚洞力学特性影响

4.1 拱顶及临时仰拱影响

在开挖阶段，为使围岩变形逐渐趋于稳定，需施作初期支护和临时仰拱，为研究拱顶与临时仰拱的沉降与变形，同将台阶长度分为5组，分别测定该台阶长度下，双洞拱顶沉降值与仰拱变形值的变化规律，并将先行洞与后行洞各项参数进行对比。

典型断面处不同台阶长度下双洞拱顶沉降值与仰拱变形值分别见图10与图11。

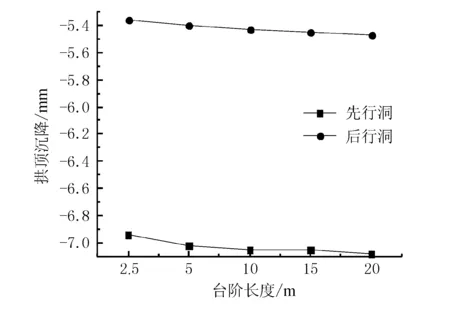
图10 典型断面处不同台阶长度下双洞拱顶沉降值

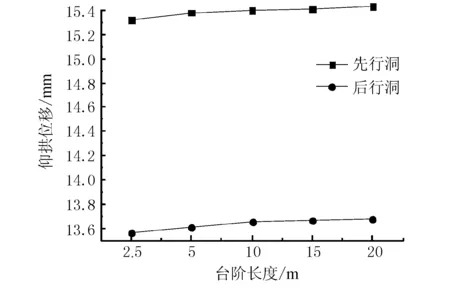
图11 典型断面处不同台阶长度下仰拱变形值

由图10、11可知，拱顶沉降值与仰拱变形值都随台阶长度的增加而有所增大，且二者的变化幅度基本保持一致。台阶长度由2.5 m增大至20 m过程中，拱顶沉降值变化率仅为2.05%，仰拱变形值变化率仅为0.81%。

综合双洞拱顶沉降值与仰拱变形值可知，台阶长度越长，先行洞与后行洞竖向收敛也呈现增长趋势，这也说明竖向上洞室向内部收敛趋势越强烈。

4.2 横向收敛的影响

以上述分组对典型断面处洞身收敛值进行测定，得到结果见图12。

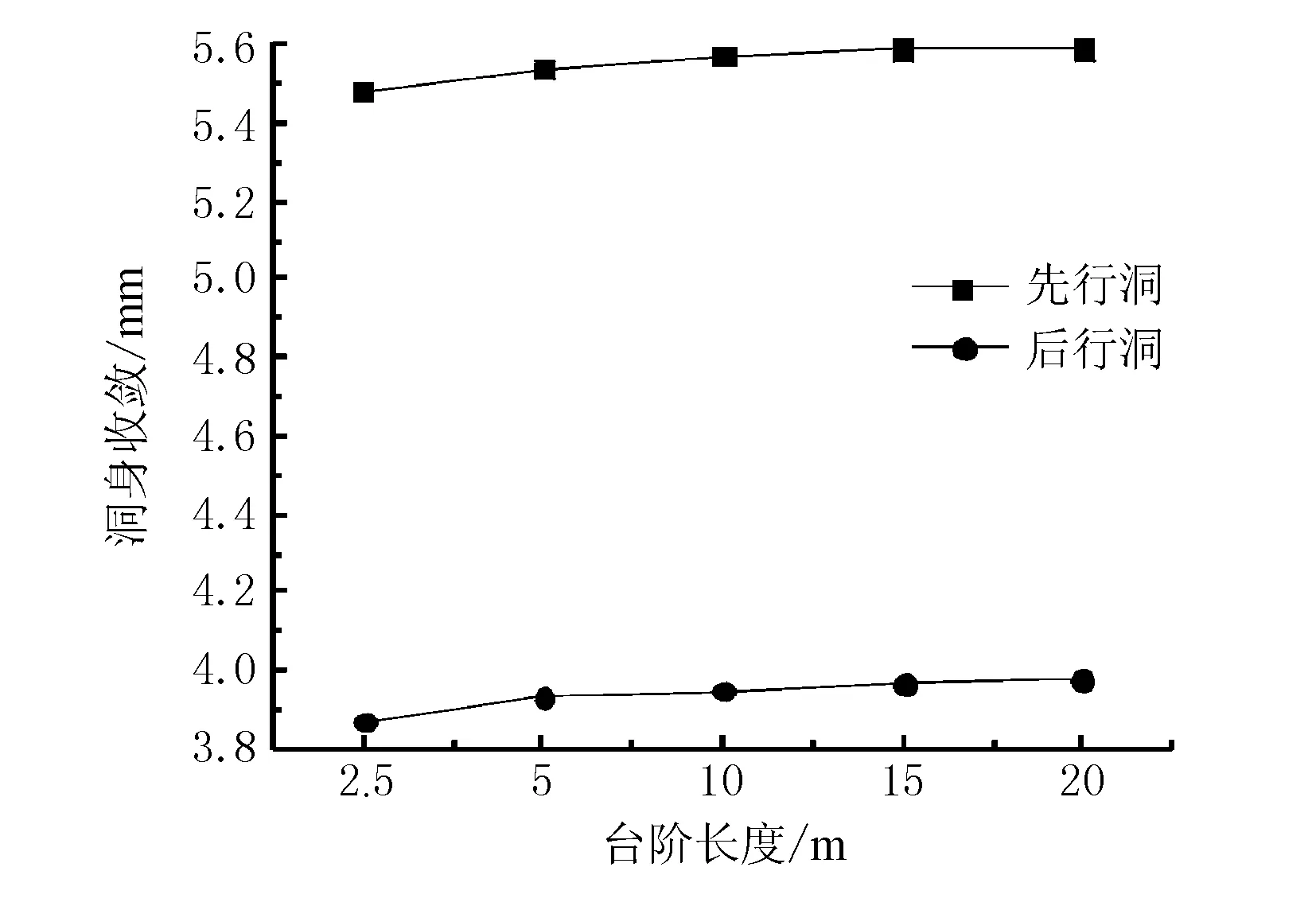
图12 典型断面处不同台阶长度下洞身横向收敛值

由图12可见，台阶长度从2.5 m增加到20 m，先行洞洞身收敛值相应地由5.48 mm增加到5.59 mm，增幅达到2.0%。由此可说明增加台阶的长度，会引起先行洞与后行洞二者洞身收敛值增大，并使得洞周围岩向内部变形呈现上升趋势。

虽然台阶长度越小，对地表沉降、横向及竖向收敛造成的影响越小，但当进行实际施工时，必须考虑施工环境的因素。若采用较小的台阶长度，会导致施工中的互相干扰增强，同时工人及机车设备的作业空间也会相应减少，不利于施工安全。为了在施工组织与围岩稳定性控制中找到一个平衡点，建议选取5 m作为台阶法开挖的台阶长度。

5 结论

本文利用数值模拟方法，研究并探讨了采用三台阶开挖法的小净距隧道锚施工参数的合理选择。并通过设置不同掌子面错距、不同台阶长度，以对比这些因素对锚洞力学特性的影响规律，以此得出合理参数的选取范围以作为具体组织施工的参照，完善施工方法。

分析以掌子面错距、台阶长度为变量进行的参数测定，得出以下结论。

1) 掌子面错距对中夹土柱沉降值的影响规律呈现出先增加再降低，最后增加并趋于稳定的趋势，先后导洞进行开挖后，锚洞临空面一侧受到围岩应力，同时中夹土柱区域受到施工扰动产生的围岩应力作用，此时表现为先行洞处中夹土柱沉降值最高。

2) 中夹土柱区几乎不受锚洞开挖的影响且掌子面错距对其影响并不显著。

3) 不同掌子面错距情况下，隧道锚中塑性区的分布基本一致，主要集中在锚塞体后半部分。掌子面错距与塑性区体积并无具体对应关系。

4) 采用台阶法开挖时，台阶长度的缩短有助于洞周围岩形成闭环，从而减少围岩变形。随着台阶长度增加，地表沉降随之增大，但地表沉降增幅逐渐减小。

5) 台阶长度能加速上洞室向内部收敛，并使得洞周围岩向内部变形呈现上升趋势。