基于改进烟花算法优化BP网络的混凝投药预测
李 赞,张长胜,田海湧,毛 辉,王 卓,马泽楠
(1.昆明理工大学 信息工程与自动化学院,云南 昆明 650500;2.云南树业科技有限公司,云南 昆明 650221;3.中国市政工程华北设计研究总院有限公司 昆明分公司,云南 昆明 650051)
在自来水厂水处理中,混凝、沉淀、过滤和滤后消毒是最重要的4个工艺。其中混凝反应[1]是整个处理过程中最为关键的步骤,混凝效果的好坏直接影响后续处理工艺设备的负担、处理成本及出厂水浊度,而混凝投药量(混凝剂量)是混凝反应的关键,投药量对混凝效果起到决定性作用。准确的投药量使得混凝效果较好,可以减轻沉淀和过滤的负担,减少投药成本,使得出厂水浊度达标。因此,混凝投药量控制是自来水厂整个处理工艺的核心问题,也是水处理专家和研究学者急需解决的问题。
Oladipupo等[2-4]提出用于水处理厂混凝控制的多模型预测控制(MMPC)策略、模糊模型预测控制(FMPC)策略及利用Takagi-Sugeno模糊推理系统开发的基于模糊切换方案的MMPC策略。Yamamura等[5]使用摄像机记录絮凝物图像,通过输入记录的絮凝物图像和浊度水平作为训练数据集,利用卷积神经网络构建用于预测上清液浊度的模型,通过提取控制絮凝物沉降性的特征能立即自动预测凝结状态,从而控制混凝剂聚合氯化铝的用量。Li等[6]阐述了人工智能的数据分析和进化学习机制,能够实现水质诊断、自主决策和运行过程优化。针对混凝投药量控制呈现出非线性多参数的特点,建立准确的数学模型有一定难度,且数学模型的适用性较差。进而,饶小康等[7]针对水厂投药工艺的特点,采用人工神经网络算法对获取的历史数据进行训练和自适应学习,并研究开发了用于混凝投药的自动控制系统。常波等[8]利用BP神经网络模型进行辨识建模。单一的神经网络预测模型对复杂水质的自适应学习较差,使得预测结果不准确,从而制约着模型的性能。随着群智能优化算法的出现,可以弥补BP神经网络的缺点。伊学农等[9]针对BP神经网络建模的缺点,提出遗传算法(Genetic Algorithm,GA)优化BP神经网络结构的投药量预测模型,对复杂水质的自适应学习、预测性能较好。GA算法在全局范围内寻优较好,但易陷入局部值,导致预测误差大,稳定性不高。
为了解决以上问题,本文将改进烟花算法(Improved Fireworks Algorithm,IFWA)引入到BP神经网络建立的混凝投药预测模型,经改进爆炸算子和精英选择策略后的烟花算法(Fireworks Algorithm,FWA)能在全局范围内寻得最优解,并结合FWA算法的高斯变异操作,跳出局部最优,利用布谷鸟搜索(Cuckoo Search,CS)算法搜索得到最优解作为FWA算法的初始烟花,提高寻优效率。经过IFWA算法搜索得到全局最优解,将其映射转化,进而寻得BP神经网络模型的最优参数,用于后续的模型训练和测试。
1 改进烟花算法
烟花算法[10]采用并行爆炸式搜索方式,在局部和全局搜索过程中具有较强的鲁棒性和寻优性,现已应用到优化调度模型[11]、预测交通流模型[12]、路径规划问题[13]、图像处理[14]、故障诊断[15]、模块检测[16]等领域。但在迭代后期,收敛速度慢,易陷入局部最优,尤其在高维复杂问题上,较为明显。针对以上问题本文提出改进算法,通过改进爆炸幅度和爆炸强度、采用精英选择策略和利用CS算法作为初始解的FWA算法,改进后的算法在寻优性能、收敛速度和精度上效果有一定提升。具体工作如下:
1.1 优化初始解
随机初始解质量差,容易导致算法性能不稳定,影响算法的适用性。CS算法[17]具有参数少、速度快、易于与其他算法相结合的优点,将CS算法搜索最优解作为FWA算法的初始解,记为优初始解,可以提高初始解的质量,对算法的收敛速度和收敛精度有较大的作用。
1.2 改进爆炸幅度
为实现爆炸在全局和局部的遍历式搜索最优值,对烟花算法的爆炸半径[18]引入爆炸幅度辨识控制因子c,如
(1)
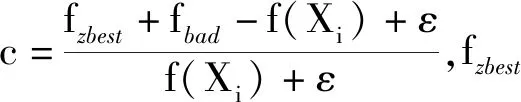
原始爆炸搜索根据适应度值的大小作为半径,逐个展开搜索,搜索效率低,且易陷入局部最优;改进后的爆炸幅度随当前迭代次数的增加而逐渐收缩,搜索效率大大提高,且控制因子c能控制和反应搜索半径的情况,既能实现高效率全局搜索,也能实现局部精细搜索,尤其加强对原点附近的搜索。
1.3 改进爆炸强度
在标准烟花算法爆炸强度中引入爆炸强度辨识控制因子q,如
(2)
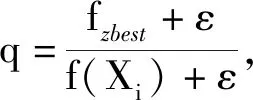
为了产生合适的火花数目,需要对火花数目用式(3)进行一定的限制:
(3)
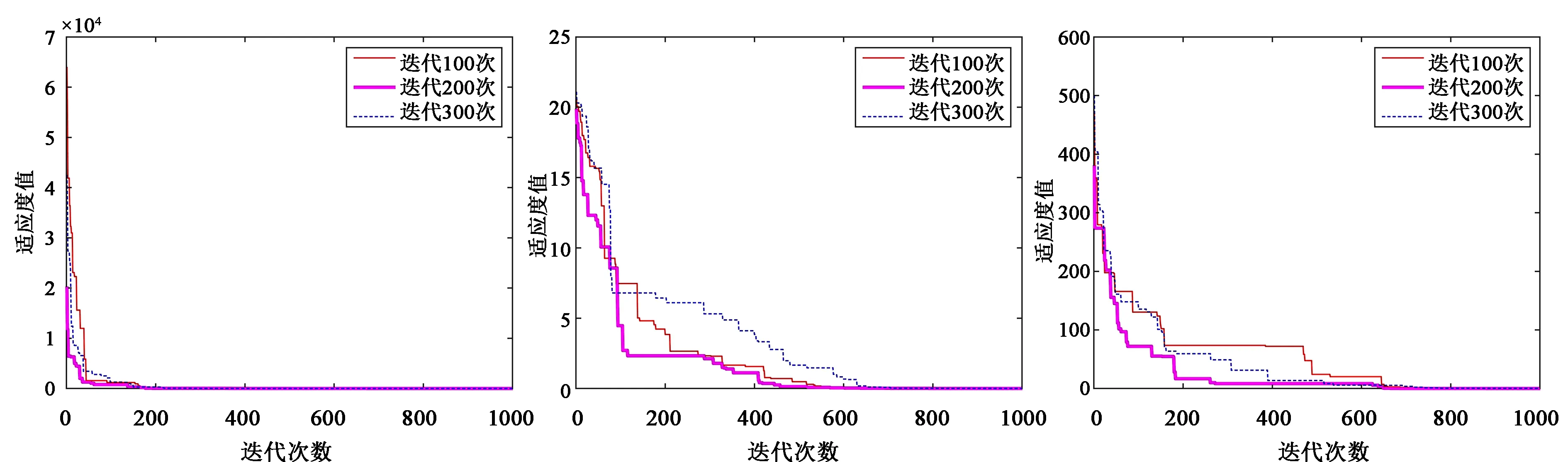
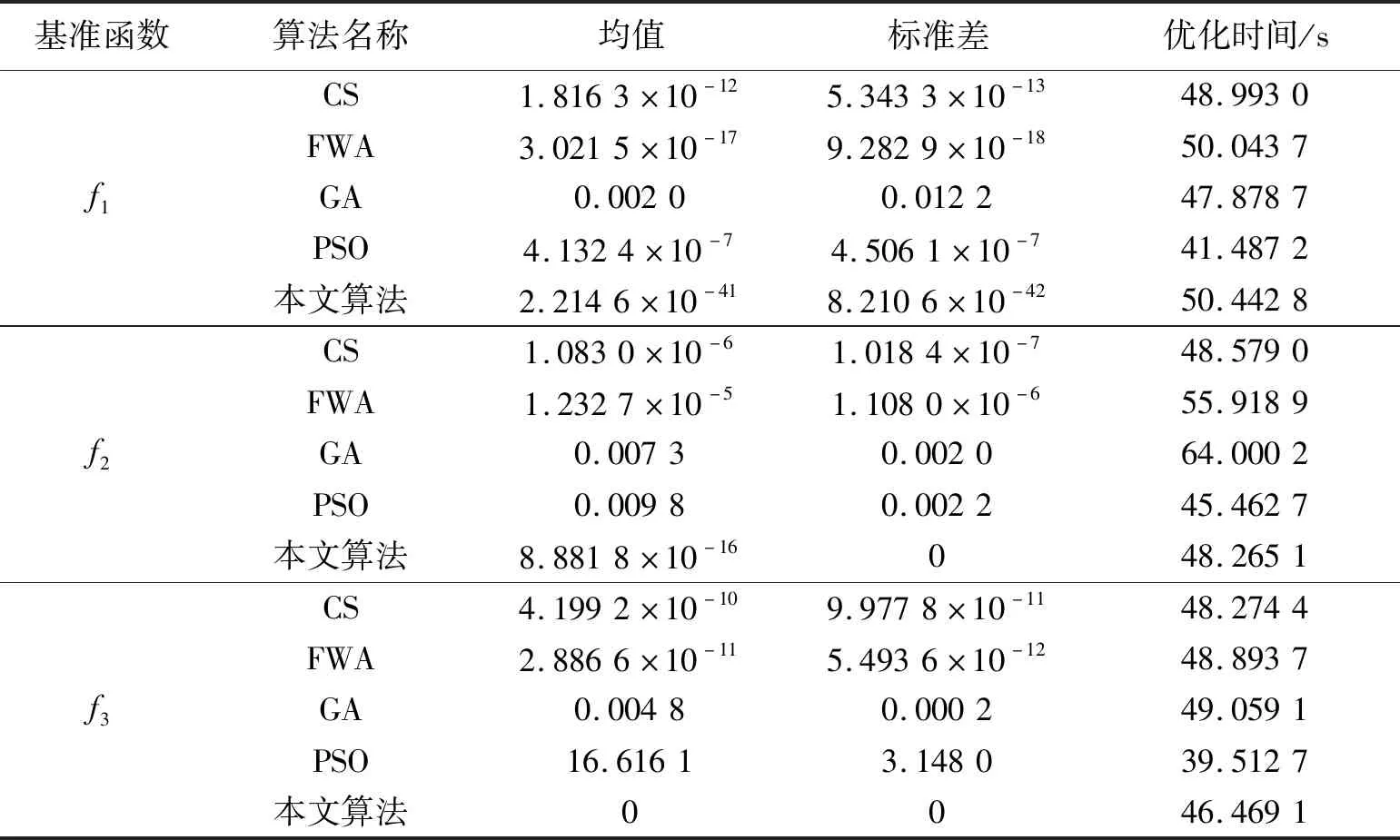
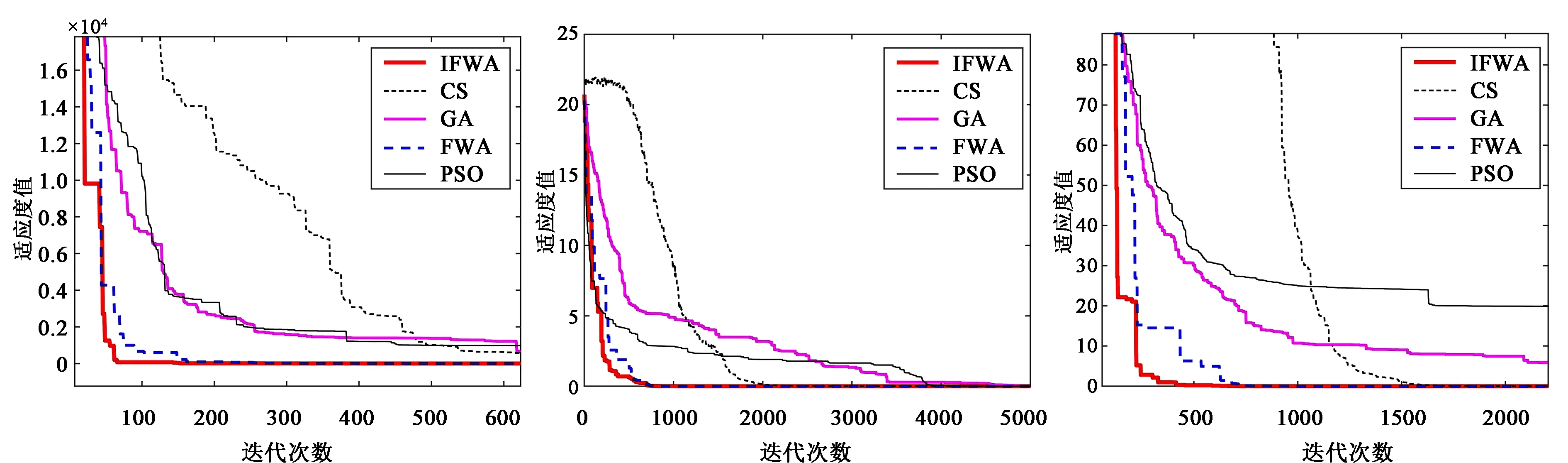
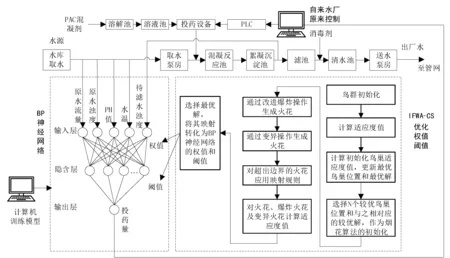
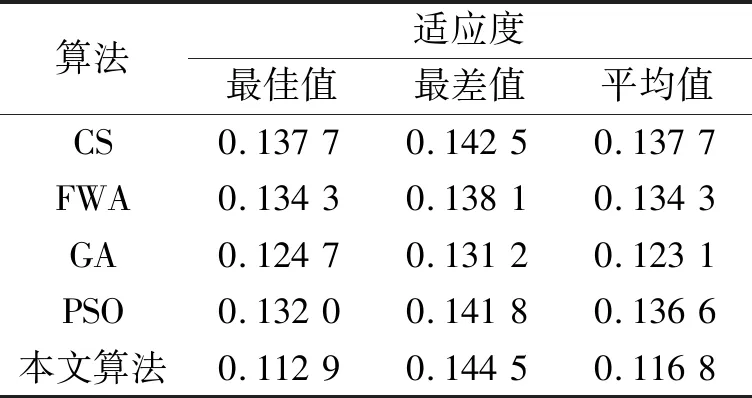
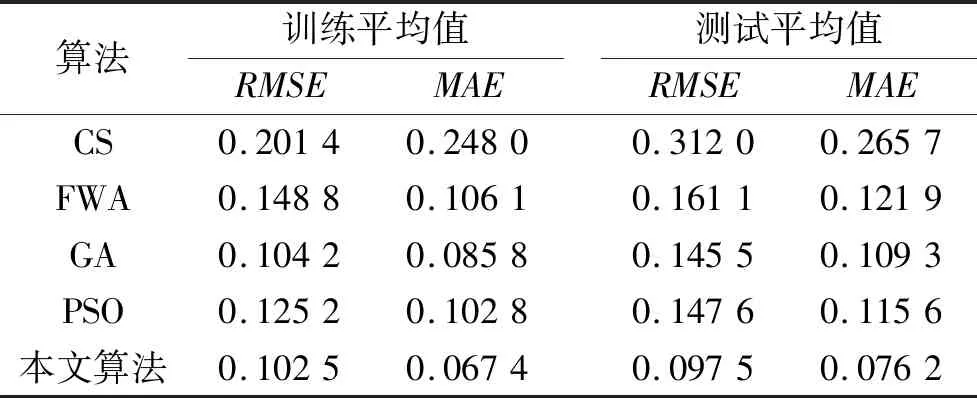
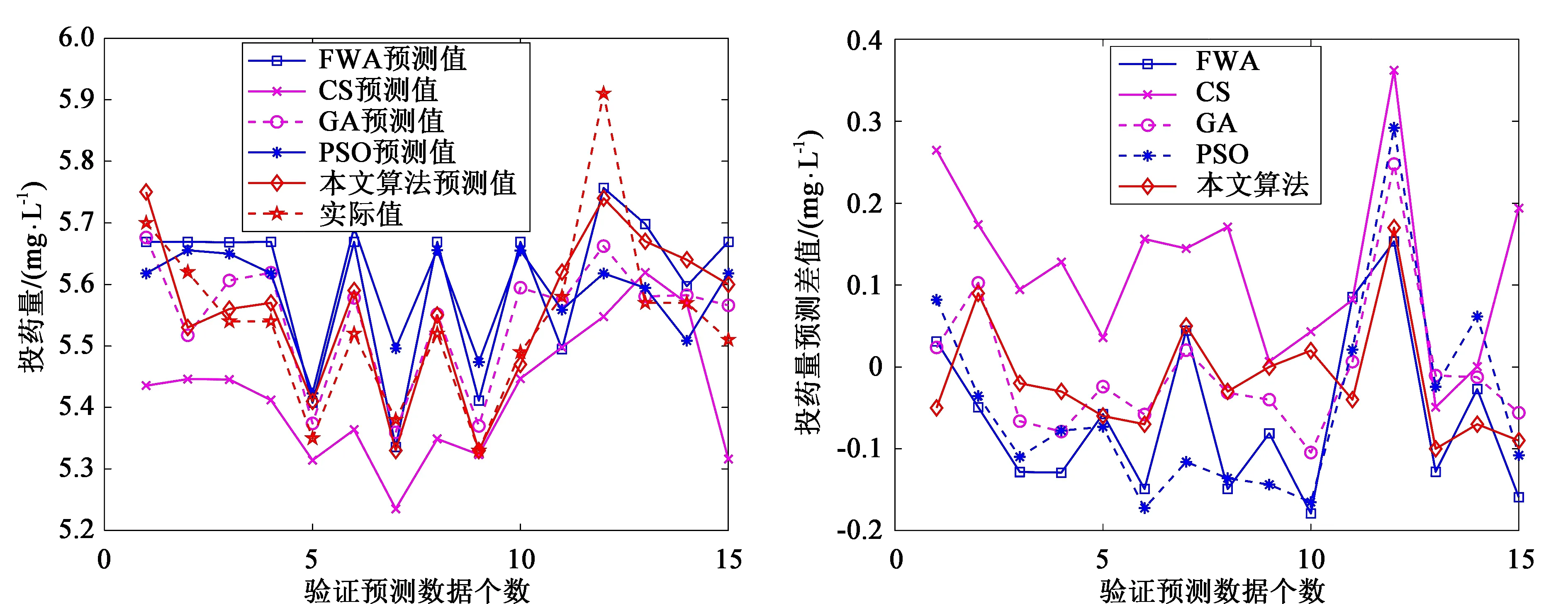
其中round()表示取整函数;a和b为给定常数,且a 传统基于距离的选择策略,离其他个体距离更远的个体具有更大的概率被选中,虽然增加了烟火种群的多样性,但可能会使得爆炸火花质量越来越差,同时增加时间成本,还影响下一代优质火花的产生。所以本文采用精英选择策略,如 (4) 式中fall(Xi)为第i个个体的适应度值。在每一次迭代中把最优烟花放入到下一代中,剩余的N-1个个体采用精英选择策略,这样可以使时间成本大大缩短,而且更容易使下一代得到优质的烟花,极大地提高了寻优效率。 本文提出的IFWA算法,其中伪代码如下: 从CS算法中取N个最优解及适应度值作为初始烟花; 初始烟花位置、最优解及适应度值/最差解及适应度值分别记为X,Xbest,fbest/Xbad,fbad。 forg=1 toTdo fori=1 toNdo 利用式(1)计算爆炸幅度; 利用式(2)计算爆炸数量; 利用式(3)对火花数量限制; end for //随机产生爆炸火花 fori=1 toNdo forj=1 toSdo fork=1:Ddo end for 保存爆炸烟花EX; end for end for //烟花高斯变异产生的火花数 fori=1 toMdo//M为烟花变异个数 fork=1:Ddo end for 保存变异烟花GX; end for 选择当前种群的X=[X,EX,GX]的烟花集合; 评估该集合烟花的适应度值,记录局部最优和全局最优值; if (f(Xi) Xi替换Xbest; end if 保留并选择最优个体作为下一代烟花; 利用式(4)的精英选择策略,选择其他N-1个烟花位置; end for 预测处理及性能评估; 为了验证本文算法的寻优能力和有效性,利用3个基准函数进行仿真测试: 其中D为维度,都是30,都在(0,0,…,0)处取得最优解0。 引入标准CS(Pa表示被宿主发现的概率或者坏蛋率)、FWA、GA(pc为种群杂交概率,pm为种群变异概率)和PSO[19](c1为个体学习因子,c2为社会学习因子,c1和c2也称为加速常数,w为惯性因子)与IFWA算法进行对比。其中在IFWA算法中,首先执行CS算法取得最优烟花,为了说明CS算法的迭代次数对FWA算法的影响,设置CS算法的迭代次数分别为100、200、300次。各算法参数设置见表1。 表1 参数设置 在IFWA算法中,当CS算法迭代次数不同时,对FWA算法的收敛效果不同,分别设置CS的迭代次数为100次、200次、300次时,对3个基准函数的影响分析,如图1所示。结果表明,CS算法的迭代次数对IFWA算法的影响,在200次时最佳,收敛速度快且能较快收敛到最优解,并非是迭代次数越大越好,到一定值后会影响FWA算法的收敛效果,还会增加时间成本。在本文实验中,IFWA算法中CS的迭代次数选为200次。 (a)f1 (b)f2 (c)f3图1 CS算法迭代次数对3个基准函数的影响 各个算法对测试函数计算10次,每次迭代5000次,收敛曲线如图2所示,其实验结果数据见表2。 表2 各算法对3个基准函数优化的结果对比 (a)f1 (b)f2 (c)f3图2 3个基准函数的收敛曲线 从上述实验中可以看出,在对3个测试函数的优化中,本文提出的改进烟花算法在精度、稳定性和收敛速度上优于标准CS、FWA、GA和PSO算法,虽然在运行时间上没有得到优化,但是提高了算法精度和稳定性等,是可接受的。然而该测试是在有限的测试函数上进行的,不可避免的会有一些片面性,需要在其他更多的优化函数或者一些复杂函数上进行完整全面的测试。 在自来水处理工艺中,影响混凝投药量有诸多的因素,受检测手段的影响,在本文中,选取进水流量(m3/h)、原水浊度(NTU)、pH值、水温(℃)、待滤水浊度(NTU)和投药量(mg/L)分别作为模型的输入输出指标。自来水厂处理工艺及网络模型预测建模流程如图3所示。从云南某自来水厂获取的历史数据,先进行预处理后再进行离线训练。对数据进行归一化处理[20],可以消除不同量纲对模型准确性造成的影响,使各指标数据处于同一量级上,从而提高数据之间的可比性。 图3 自来水厂处理工艺及网络模型预测建模流程 根据选取的输入输出指标,得知BP神经网络[8]的输入层为5,隐含层为7,输出层为1,节点传递函数为logsig,训练函数为trainlm,学习函数为learngdm,训练最大迭代次数为5000,网络学习率为0.01。 采用训练集和测试集的均方根误差的平均值作为适应度值,可降低过拟合的概率。适应度函数为 (5) 式中f(Xi)表示第i个烟花的适应度值,t和v分别为训练集和测试集的个数,Tl和Pl分别为第l个训练集的实际值和预测值,Tm和Pm分别为第m个测试集的实际值和预测值。 利用MATLAB R2018b软件搭建实验仿真平台,根据云南某自来水厂提供的1000组数据,对IFWA算法优化BP神经网络的自来水投药量预测模型进行编程实现以及对预测模型的有效性进行仿真验证。 为了验证IFWA算法优化BP神经网络模型在自来水投药量预测方面的预测性能,在各训练参数条件下,采用相同的训练集(900组)和测试集(100组),分别对基于CS、FWA、GA、PSO及IFWA等算法优化BP神经网络的投药量预测模型进行离线训练和测试。以f(Xi)为适应度函数,在不同算法的情况下重复寻优10次,取最佳值、最差值及平均值,见表3。结果表明,以适应度值的最佳值、最差值及平均值为性能指标,综合得出基于IFWA算法的预测模型较好,GA算法其次。 表3 算法适应度值 表4 算法训练和测试性能指标 最后,分别选取15、50、100组数据进行验证预测测试,通过仿真实验,得到了不同算法优化BP网络模型的投药量预测结果,均表明还是IFWA算法的最好。为了避免线条繁杂,绘制出的图形杂乱,影响美观,使用15组测试数据绘制对比结果予以直观说明,图4为各算法预测投药量对比,图5为各算法预测投药量差值。 图4 各算法预测量对比分析图 图5 各算法预测量差值 从图4中反应了基于各算法模型的预测值与实际值的曲线情况,其中基于IFWA算法的模型预测出的测试数据与原数据的拟合度较好,数据有波动但幅度小;图5反应了实际值与预测值之间差值的变化情况,其中IFWA算法模型的预测值与实际值之间差值的变化幅度小,优于CS、FWA、GA等算法。 针对自来水厂混凝投药量控制的缺点,本文将IFWA算法引入到BP神经网络模型,提出了一种IFWA算法优化BP神经网络的混凝投药量预测模型,利用云南某自来水厂的数据对该模型进行训练、测试。其仿真结果表明: (1)由测试函数结果可知,改进初始烟花算法、爆炸算子和选择策略后的烟花算法,优化精度、寻优能力、收敛速度比标准CS、FWA、GA等算法好。 (2)在自来水厂混凝投药量预测模型中,以RMSE和MAE为指标,说明本文提出的基于IFWA算法优化BP神经网络的混凝投药量预测模型的预测精度优于基于CS、FWA、GA等算法建立的BP神经网络预测模型,且前者预测的RMSE约为0.097 5,MAE约为0.076 2,预测效果最优。 (3)基于本文提出的IFWA算法建立的BP神经网络预测模型在预测精度和收敛速度上较好,对自来水混凝投药具有一定的指导意义。 (4)在后续研究中,可考虑碱度、色度、TOC(有机物含量)、电导率等更多影响混凝投药量计算的输入因素,并对本文改进算法进一步优化,以提高预测精度及降低时间复杂度。1.4 精英选择策略
1.5 IFWA算法
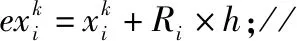
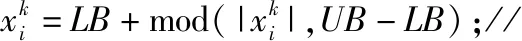
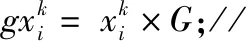
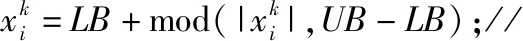
1.6 函数测试

2 建立自来水混凝投药预测模型
2.1 确定输入输出指标
2.2 BP神经网络及算法的关键参数
2.3 选择适应度函数
3 仿真结果及分析
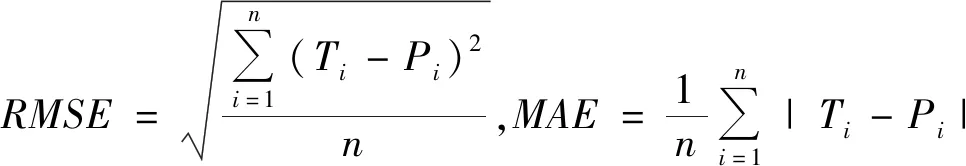
4 结论

