率熵函数
徐大专,刘 甜
(南京航空航天大学电子信息工程学院,南京 211106)
引 言
率失真函数是信源编码的理论下界,已成为信源数据压缩的理论基础。率失真的思想最早来源于香农在1948年发表的经典论文[1]。不久后,前苏联的Kolmogorov[2]在1956年开始发展率失真理论。Shannon于1959年系统地阐述了率失真理论[3],并证明了第一率失真定理。对于更一般的信源,Berg‑er[4‑5]完善了信息率失真理论和限失真的信源编码定理。1972年,Blahut[6]将计算信道容量的迭代算法成功地用于计算离散信源的率失真函数。
随着通信网络、特别是移动通信技术的进步,率失真理论也在向网络化方向发展。在分布式信源编码方面,最经典的结果是Berger[7]和Tung[8]给出的内界。尽管Berger‑Tung问题到目前为止仍然维持开放,但其中部分问题已经得到解决。在汉明失真条件下,Slepian和Wolf[9]、Ahlswede和Korner[10]、Wyner[11]给出不同情形下的可达码率区域。Berger和Yeung[12]则给出更一般的解。
针对均方失真条件下的高斯信源,Oohama[13]给出带边信息的率失真区域。针对Berger等提出的编码器不能直接观测到信源,而只能观测受到噪声干扰信源的CEO(Chief executive officer)问题,Prab‑hakaran等[14]、Oohama[15]分别独立地得到高斯CEO问题的率失真区域。Wagner等[16]进一步解决了带边信息的CEO问题,从而,最终完全解决了高斯Berger‑Tung问题。东南大学的徐寅飞[17]在其博士论文中解决了迹失真约束下的向量高斯CEO问题。
目前,关于限失真信源编码的率失真函数理论尚存在一些问题没有解决。首先,率失真函数本质上是一个约束变分问题,求解本身较为复杂,目前只有为数不多的信源可求得率失真函数的闭式解。均匀分布是最常见的信源,商用的模数变换器都是针对均匀分布信源设计的,但其率失真函数尚不可知。其次,对给定信源采用何种失真准则并无定论,比如高斯分布信源通常采用均方失真准则,那么,能否采用绝对值失真准则呢。在多维情况下,失真函数问题更加复杂,比如,既有矩阵失真准则,也有迹失真准则等不同形式。
率失真函数都是在编码侧定义的,但一个有趣的现象是,实际信源编码器设计往往从译码侧出发,比如著名的Lloyd算法就是基于译码器平均失真最小化设计的。这种从译码侧定义失真度的思想与作者在空间信息论中提出的熵误差[18]概念不谋而合,参数估计方法的性能就是用后验熵或后验熵误差评价的。本文以译码器的条件微分熵作为不确定度准则,提出信息率‑微分熵函数的概念,以下简称率熵函数。虽然率熵函数定义为互信息的约束变分问题,但可以通过构造变分问题的特解求率熵函数的闭式解。
本文提出了构造变分问题特解的4种方法,即熵不变准则、独立误差准则、再生性准则和弱再生性准则。据此得到目前常见概率分布的率熵函数闭合表达式,包括均匀分布、具有再生性的概率分布、向量高斯分布以及存在特征函数和熵函数的分布。
率熵函数中的不确定度H不满足非负性,因此,不确定度并不满足失真函数的定义。将不确定度通过幂指数的形式映射成非负实数D(H),可以得到广义失真测度。这种广义失真测度具有明显的优越性,高斯信源的广义失真测度自适应于均方失真准则,而拉普拉斯信源的广义失真测度自适应于绝对值失真准则。针对向量高斯信源,广义失真测度则自适应于误差协方差矩阵的行列式,既不同于矩阵失真测度,也不同于迹失真测度。
1 率失真函数和率熵函数
1.1 率失真函数定义
设连续信源X的概率密度函数(Probability density function,PDF)为p(x),描述编码器的条件信道为编码输出信宿的PDF为̂之间的失真函数为非负实数,平均失真为dˉ=平均失真满足的所有试验信道集合为则信息率失真函数,或率失真函数定义为

式中inf(⋅)表示下确界。失真函数的具体形式由实际应用场景确定,常见的失真函数采用平方失真对应的平均失真度分别称为均方失真准则和绝对失真准则。
率失真函数定义为互信息的约束变分问题,下确界的求解十分复杂,目前只有高斯分布等少数几类信源的率失真函数存在闭式解。或绝对值失真
1.2 率熵函数定义

信息率熵函数(下称率熵函数)与率失真函数的不同主要表现在如下两方面:
(1)率失真函数从编码侧定义,而率熵函数是从译码侧定义的。

求解变分问题,而是试图构造译宿分布的特解满足式(4),且达到下确界。

定理1指出,求率熵函数不一定非求变分不可,只要在集合GH中寻找达到下确界的特解。下面的推论进一步缩小求解的范围。

推论1.1的条件是译码器的不确定度处处相等,而与信宿无关。
考虑率熵函数R(H)的定义域。由互信息的非负性,必有H≤h(X)。由于译码器的微分熵有可能为负值,故H∈(-∞,h(X)]。可以证明率熵函数R(H)有以下性质:
(1)非负性R(H)≥0,等号成立当且仅当X̂和X相互独立;
(2)R(H)是H的单调下降函数。
2 均匀分布信源的率熵函数和率失真函数
均匀分布是最常见的概率分布,然而,均匀分布信源的率失真函数至今尚不清楚。设均匀分布信源的PDF为

式中H=log2Δ。如果用Δ=2H表示失真度,那么,均匀分布信源的率失真函数为

这里失真度Δ=2H既不是均方失真,也不是绝对失真,而只是译码器微分熵的指数函数。这就是传统方法无法求解率失真函数的原因。
率失真函数R(Δ)与传统率失真函数有类似的特性,比如
(1)定义域为Δ∈(0,2h(X)],当Δ→0,R(Δ)→∞;当Δ=2h(X),R(Δ)=0。
(2)R(Δ)是Δ的单调下降函数。
3 再生信源的率熵函数和率失真函数
具有再生性的概率分布有很多,如高斯分布和柯西分布等,本文称概率分布具有再生性的信源为再生信源。再生信源的率熵函数和率失真函数存在简单的求解方法。

推论2.1设信源X的概率分布p(x)具有再生性,则X的率熵函数为R(H)=h(X)-H。

式中:失真度D仅仅是与微分熵对应的一个参数,在推导过程中并未定义率失真函数的具体形式。
算例2柯西分布信源的率失真函数
设柯西信源的概率分布p(x)服从柯西分布,即
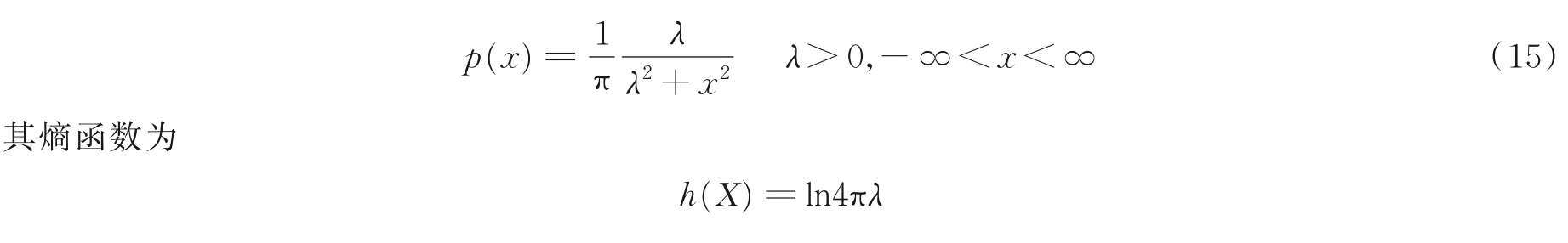

由于柯西分布不存在一阶及以上统计量,因此,这里的熵幂失真度既不是绝对失真,也不是均方失真,而仅仅反映柯西分布的尺度参数。
柯西分布的率失真函数如图1所示,它的定义域为(0,λ],图为λ=6的情况。当D→0时,信息率趋于无穷,这与连续信源的绝对不确定性为无穷大一致。随着熵幂失真度增加,信息率呈指数下降。当D→λ时,信息率等于零,这表明当熵失真度足够大时,不需要传输任何信息量。
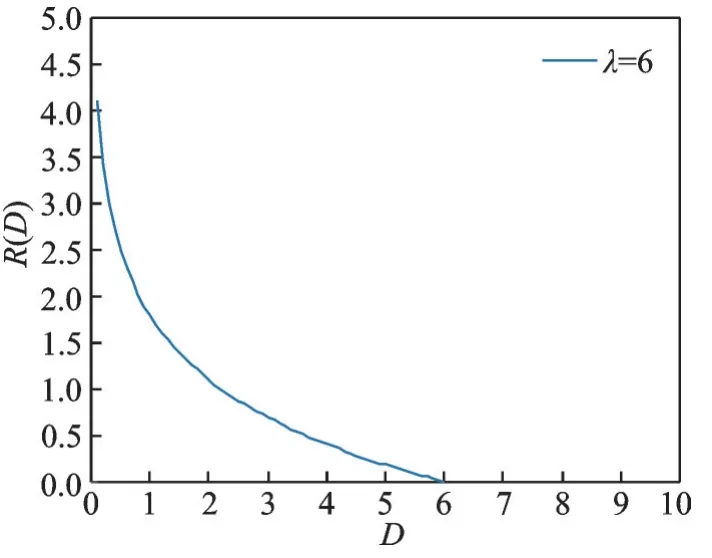
图1 柯西信源的R(D)函数曲线Fig.1 R(D)function of Cauchy source
算例3向量高斯信源的率失真函数
设N维向量高斯信源的PDF为
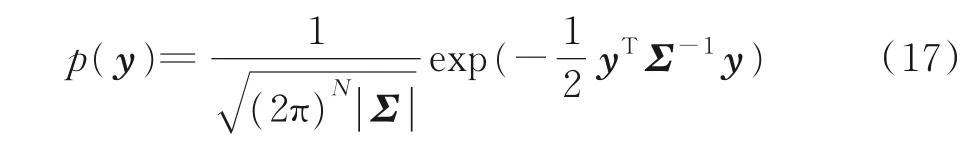
式中Σ为满秩协方差矩阵。信源的微分熵为



表1 再生信源的率熵函数Table 1 Rate entropy functions of regenerative sources
4 弱再生信源的率失真函数
再生信源只有少数几种,绝大多数信源不满足再生性条件。为此,放宽再生性条件为


4.1 拉普拉斯信源的率熵函数
设拉普拉斯信源(后简称拉氏信源)的PDF为


式中δ(x)为单位冲激函数。
X̂的PDF在0点出现单位冲激函数是由于拉氏分布在0点不光滑导致。虽然̂的PDF含有冲激函数,但X̂的概率分布函数

由定理1,拉氏信源的率失真函数

式中D即为拉氏信源的熵幂失真度。
由于拉氏信源不是再生信源,译码器仍然采用弱再生性假设比较生硬,信宿中出现冲激函数可以看成是对这一处理方法的抗议。由弱再生假设得到的仅仅是译宿分布的一组特解,有可能存在其他性质更好的解。
4.2 几种常见信源的弱再生性
特征函数的逆变换也是傅里叶变换,存在的充要条件是特征函数φΘ̂(t)满足Dirichlet条件:
(1)φΘ̂(t)绝对可积;
(2)φΘ̂(t)具有有限个极值点;
(3)φΘ̂(t)连续或具有有限个第一类间断点。

由于贝塞尔函数是连续的,因此,φX̂(t)满足Dirichlet条件(3)。由于I|t|(D)函数非负,因此,对任意给定的变量,特征函数φX̂(t)<∞是有界的。另外,当D≤κ时

故特征函数满足Dirichlet条件(2)。虽然不知道φX̂(t)是否满足绝对可和条件,但如果允许其逆傅里叶存在冲激函数,那么,虽然还不能得到
冯·米塞斯分布的微分熵有闭合表达式,即

表2给出几种常见概率分布的特征函数和微分熵,表3给出几种常见概率分布的率失真函数。

表2 几种常见概率分布的特征函数和微分熵Table 2 Characteristic functions and differential entropy of several common probability distributions

表3 几种常见信源的率失真函数Table 3 Rate distortion functions for several common sources
5 结束语
本文从译码侧提出了率熵函数的概念,并给出严格定义,其中熵失真度也是一种平均失真。为求解信源的率熵函数,提出了构造变分问题特解的4种方法,并得到了包括均匀分布在内的常见概率分布的率熵函数闭合表达式。为解决熵失真度不满足非负性问题,提出了熵幂失真度的概念,此失真度能更好地反映信源的统计特征,如,对于正态分布信源,熵幂失真度等于均方误差(二阶统计量),对于指数分布信源则等于绝对值误差(一阶统计量)。对于柯西分布,由于它不存在一阶及以上统计量,因此,绝对失真度和均方失真度都不存在。本文中柯西分布的熵幂失真度就是其尺度参数,从而避免了传统率失真函数定义问题。
本文是关于率熵函数的第一篇论文,率熵函数与率失真函数之间的关系尚未得到充分研究。率熵函数在分布式信源编码、多终端信源编码和多层描述编码等领域的研究工作未及展开,一系列重要理论问题有待进一步研究,期望得到信息论学界的高度关注。

