填埋场渗漏条件下的自然电位响应特征及影响机制
能昌信, 杨 健, 徐 亚, 赖凯伦, 刘 凡, 刘景财
1.山东工商学院信息与电子工程学院, 山东 烟台 264005 2.中国环境科学研究院固体废物污染控制技术研究所, 环境基准与风险评估国家重点实验室, 北京 100012

然而在介质渗漏的动态监测领域中,目前相关研究还比较少. 郭秀军等[26]综合运用电阻率法、自然电位法、探地雷达以及化学分析的方法,通过对污水管道污染区分布特征的研究成功进行了渗漏点定位. Martínez-Pagán等[27]利用自然电位法监测了盐水在沙箱中的扩散,定位了泄露源以及污染物羽流.
相较于自然电位法在上述场景中的应用,填埋场渗漏由于漏点上方作用水头小、下方黏土衬垫或天然基础层防渗性好等原因通常以低速渗漏;同时又由于漏点深、埋藏隐蔽难发现,呈长期持续渗漏态势,与污水管道等快速短期泄露特点存在差异. Arisalwadi等[28]开展了填埋场渗漏的自然电位法探测,但仅基于现场的自然电位法数据描述了特定填埋场渗漏条件下的自然电位异常现象,没有深入揭示渗漏量与自然电位异常的定量关系及影响因素. 为此,该文拟以模拟填埋场为研究对象,基于填埋场实际地质特征,构建一个中等尺寸的物理模型;分析在填埋场渗漏条件下的自然电位特征,以验证自然电位法在该场景下的适用性,并在此基础上实现对渗漏点的精准定位;进一步量化研究渗漏速率与电位异常的响应关系,继而得出能与之响应的渗漏速率下限;最后基于电极(不极化电极和极化电极)对自然电位响应的不同,比较电极之间的灵敏度及抗噪声性能,以期为将自然电位法用于填埋场渗漏检测领域提供参考.
1 模型与方法
1.1 模拟填埋场地构建
模拟填埋场地尺寸为700 cm×600 cm×50 cm(见图1),对该试验场地的边坡和底部(除模拟漏洞处以外)均采用防渗混凝土进行防渗处理以模拟实际填埋场防渗结构. 模拟漏洞设置在边坡40 cm深度,大小为4 cm×4 cm,不进行任何防渗处理,以模拟漏洞存在下渗滤液的渗漏情况. 实际填埋场在库底和边坡处通常均采用HDPE膜和黏土形成复合防渗,正常情况下渗滤液通过HDPE膜漏洞并经黏土衬垫渗漏的量极小,除非黏土存在裂缝或黏土衬垫与HDPE膜连接处存在较大孔隙等渗流优先通道. 因此在模拟漏洞位置处铺设一段宽20 cm、高15 cm的卵石颗粒,模拟高渗透性优先通道. 根据GB 16889—2008《生活垃圾填埋场污染控制标准》[29]等规定,黏土衬垫大于200 cm厚度,因此将高渗透性通道长度设置为260 cm. 另外,为防止模拟渗滤液流入环境中,对周边环境造成影响,在该通道下游位置设计有一个渗滤回收池.
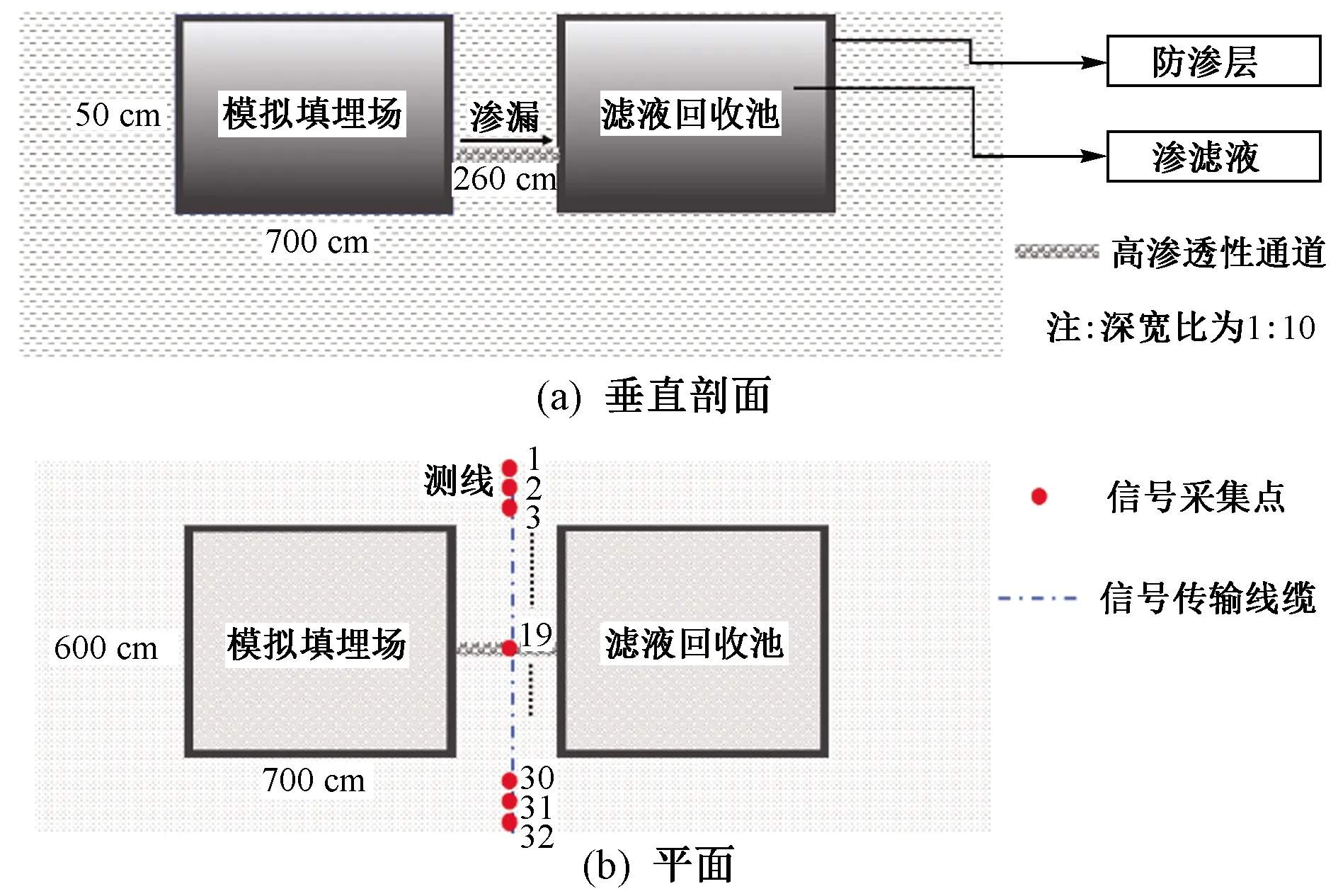
图1 填埋场渗漏场地几何结构示意Fig.1 Geometric structure diagram of leakage in landfill
根据文献报道的国内填埋场HDPE膜漏洞数据,漏洞密度的中位值达到27个/hm2(以半径为1 mm 计算)[30],等效于一个库底面积为1 hm2的填埋场中存在一个半径为27 mm的大漏洞. 根据式(1)可以得到通过该漏洞的渗漏速率约为0.01 m3/s. 该文将模拟渗漏速率设置为0.002 m3/s,模拟分析在渗漏速率等于中位值的20%条件下的自然电位特征,渗漏速率通过蠕动泵调节控制. 渗漏流体的组分也会影响渗漏条件下的自然电位响应特征,暂不考虑复杂渗滤液组分的影响,因此选用市政中水作为模拟渗漏流体.
Q=Cbπr2(2ghw)1/2
(1)
式中:Q为渗漏速率,m3/s;r为漏洞半径,m;Cb为形态系数,一般取0.6;hw为饱和液位高度,取3 m;g为重力加速度,9.8 m/s2.
1.2 信号采集装置
自然电位信号采集的测线布设于模拟填埋场地和收集池的水平中心位置〔见图1(b)〕,由间距30 cm的32个采集点组成.
自然电位法采集系统采用自主开发的采集系统,由硬件和软件两个部分组成[31-32](见图2). 硬件模块的功能为信号的滤波及采集,其中电极转换器采用DAM3200继电器,采集装置选用NI-9205采集卡,利用检测电极观测勘探区域的自然电位信息,经过滤波装置及采集装置实现对信号的采集. 软件模块由LabVIEW平台搭建,由串口控制模块、采集、处理模块和数据保存模块组成,在此基础上发送采集指令对继电器进行控制,实现电极采集功能.
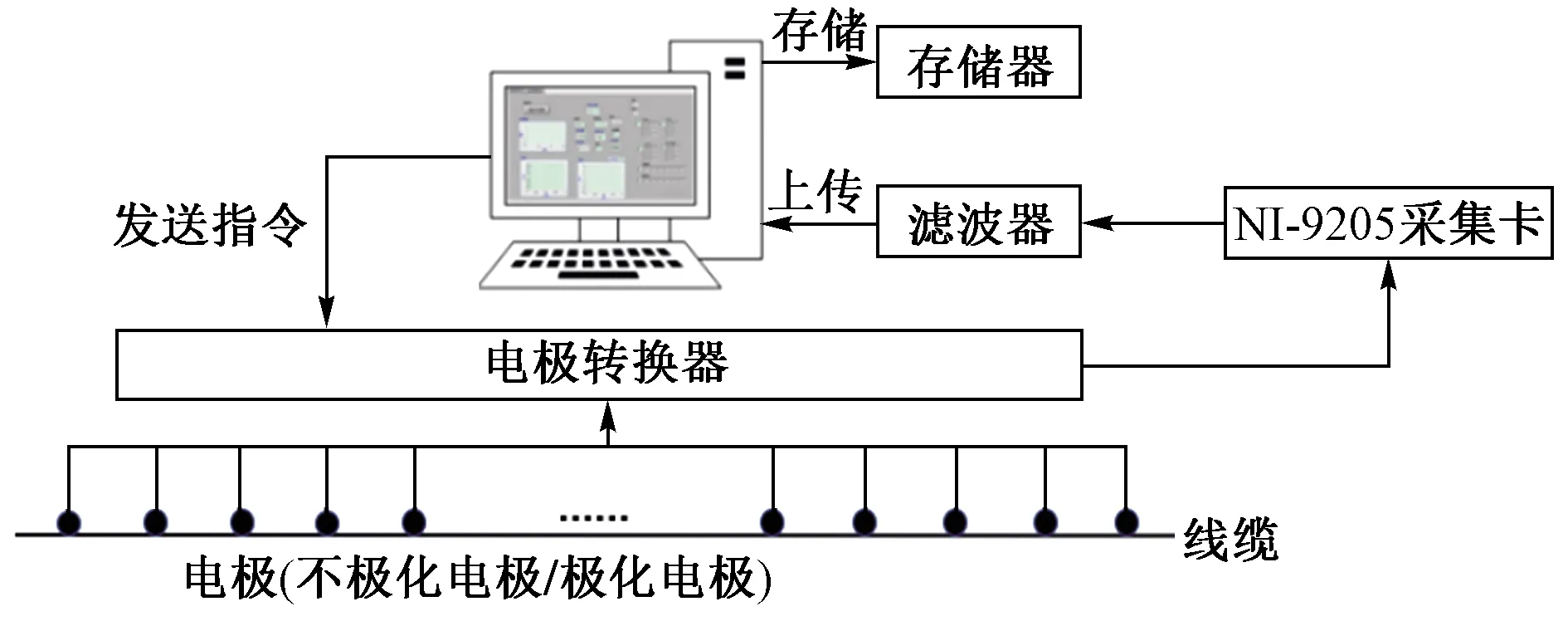
图2 信号采集系统组成Fig.2 Signal acquisition system composition
1.3 试验过程
在模拟试验之前,为描绘模型的初始自然电位特征以及滤除噪声信号对自然电位特性的干扰,在1 h内采集3次背景自然电位.
在背景值采集完成后,利用蠕动泵向模拟填埋场中注水,由于高渗透通道具有良好的渗透能力,使得在高渗透通道内的渗滤液渗漏速率基本等于由蠕动泵所提供的注水速率;根据1.1节分析结果,设置渗漏速率为0.002 m3/s,即200 mL/s. 注水过程中,以30 s为间隔对自然电位进行连续采集和监测,观测到自然电位达到稳定状态后,保持200 mL/s的恒定渗漏速率10 min后停止供水;停止注水后,继续进行自然电位采集和监测,直至回收池中不再有水流入.
为研究不同电极对渗漏时产生的自然电位特征响应,在测线上布置不极化电极(消除极化电位)的同时,在距其0.2 m处平行布置极化电极同步进行信号采集;另外,为表征渗漏速率对自然电位的异常响应强度关系,设置了3组不同模拟渗漏速率的试验(见表1). 同样由蠕动泵提供注水速率以模拟渗漏速率,并以30 s为间隔对自然电位进行连续采集和监测.

表1 3种不同渗漏速率及持续时间
2 结果与讨论
2.1 渗漏条件下自然电位的时序变化和电位异常
2.1.1不同位置处自然电位的时序变化
模拟渗漏发生前及发展过程中不同时刻测线上各采集点自然电位的时序分布如图3所示;另外,为分析在试验过程中自然电位的时序变化程度,对不同时刻各采集点的自然电位进行时序方差计算.
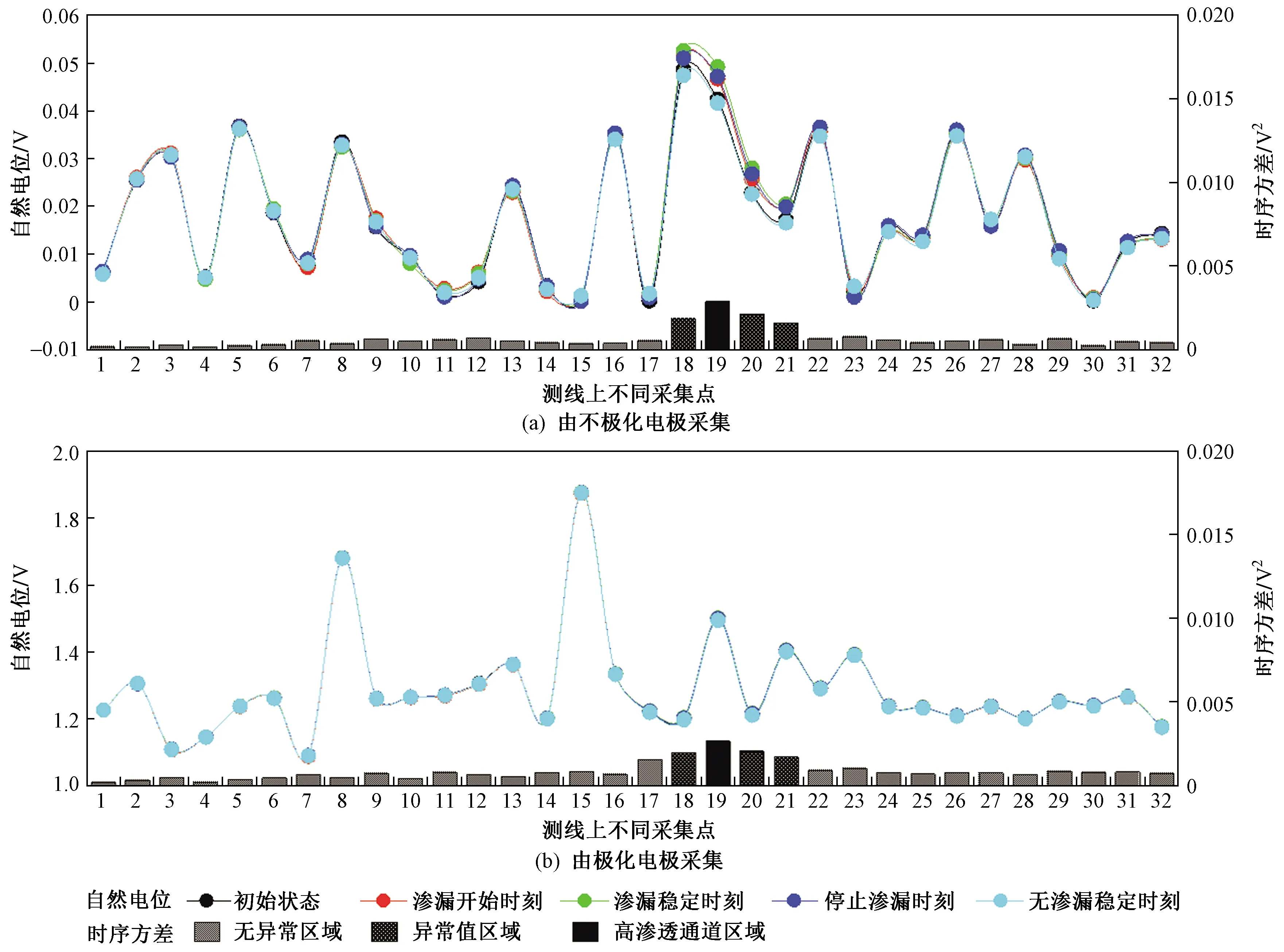
图3 不同渗漏条件下测线上各采集点自然电位的时序变化Fig.3 Time-series variation of self-potential at each electrode under leakage condition
在利用不极化电极和极化电极采集自然电位时,不极化电极消除了极化电位,使之保持不极化状态;反之,极化电极检测出的自然电位包含了极化电位. 由图3可见,不极化电极检测出自然电位的尺度为10-2,极化电极检测出自然电位的尺度为100,而渗漏所引起自然电位异常的尺度为10-3;自然电位与异常电位相差了较大的数量级,因此直接观测自然电位分布并不能很明显地表征电位异常[33]. 以图3(a)所示结果为例,自然电位时序方差随着采集点与渗漏区域之间的距离变化呈现一定的趋势性,距离越小时自然电位时序方差越大. 在19号采集点处自然电位时序方差达到 0.003 0 V2,在18号和20号采集点处分别为 0.001 8 和 0.002 1 V2,而在远离渗漏区域处自然电位时序方差多在 0.000 5 V2左右. 时序方差用于衡量随机变量或一组数据的离散程度或变异程度,时序方差越大,说明其变异程度越大[34]. 该研究中,自然电位的时序方差越大,说明由渗漏所引起的自然电位异常也越大,渗漏的产生使得渗漏区域(19号采集点)及其附近产生了电位异常[35],同时在远离渗漏区域处自然电位无明显变化. 鉴于采集点处自然电位时序方差与渗漏区域的距离之间存在良好的响应关系,在利用自然电位法进行渗漏监测过程中,相较直接观测测线各采集点的自然电位分布而言,根据各采集点自然电位时序方差的峰值能更直观、精准地定位渗漏区域.
2.1.2渗漏通道上方的自然电位异常
为进一步量化分析自然电位异常与渗漏区域之间距离的关系,绘制了19号(渗漏通道正上方)、1号(远离渗漏通道)、18号(渗漏通道左侧)和20号(渗漏通道右侧)采集点处自然电位的时序变化图. 由图4(a) 可见,在由不极化电极采集的条件下,由于其远离渗漏区域,在整个模拟试验过程中,1号采集点处的自然电位始终保持在 0.006 3 V左右的近似稳定状态. 反之,在渗漏区域上方的19号采集点处,自然电位在试验初期恒定在 0.042 8 V左右后,产生了由渗漏导致的自然电位异常,最大值达到 0.006 8 V,增加了16.1%,当停止渗漏时,由于渗漏速率的衰减,自然电位异常现象逐渐消失,渗漏区域自然电位也逐渐衰减至背景值状态. 同时,由于渗漏对邻近采集点的影响,在18号和20号采集点处分别引起了 0.002 5 和 0.002 4 V的最大自然电位异常.
该研究表明,渗漏区域会对周围采集点产生与距离成反比的自然电位异常,这与点电流源对地层内部产生的电位所表征的物理规律相一致,点电流源对地中的电位由式(2)所表征,那么可以将渗漏点近似看作一个“点电流源”[36],对渗漏点进行定位也就是对“源”的定位.
(2)
式中:U为电位,V;I为电流,A;ρ为电阻率,Ω·m;R为点源与采集点之间的距离,m.
利用控制变量法将不极化电极替换为极化电极后,渗漏产生自然电位异常的规律保持不变〔见图4(b)〕,渗漏区域对周围采集点产生的自然电位异常与距离成反比. 随着渗漏区域与采集点之间距离的变化,在远离渗漏区域的1号采集点处并未产生自然电位异常;在渗漏区域上方的19号采集点处,随着渗漏产生而引起的自然电位异常的最大值达到 0.003 0 V;此外,在渗漏区域左、右采集点处最大自然电位异常分别为 0.002 0 和 0.002 2 V.
试验结果表明,当渗漏速率为200 mL/s时,渗漏区域产生了最大值为 0.006 8 V的自然电位异常,表明自然电位能作为渗漏的响应指标. 进一步研究发现,由于自然电位与由渗漏引起的自然电位异常存在较大的数量级差异[37],直接观测自然电位分布不能直观地对渗漏区域进行定位;而通过计算时序方差则可以根据时序方差峰值实现对渗漏区域的精准定位,在渗漏区域处的时序方差达到 0.003 0 V2. 另外,通过对渗漏通道及其周围的自然电位异常进行量化分析,渗漏区域会对周围采集点产生与距离成反比的自然电位异常,则可将渗漏点近似看作一个“源”,为后续对渗漏点的垂直定位提供一定的理论基础.
2.2 渗漏速率对自然电位的影响
2.2.1不同渗漏速率下自然电位的时序变化
在3种不同渗漏速率条件下,绘制了在模拟渗漏发生前及发展过程中不同时刻各采集点处自然电位的分布情况(见图5),以及对其进行方差计算得出时序方差. 以图5(a)所示结果为例,在低渗漏速率(43.48 mL/s)条件下,不极化电极并未响应出自然电位异常;而在102.04和166.67 mL/s渗漏速率下〔见图5(b)(c)〕,在渗漏区域及其附近区域产生了自然电位异常,其时序方差峰值与相应渗漏速率下的渗漏区域重合,时序方差峰值分别达到 0.001 0 和 0.001 6 V2,表明根据测线上各采集点处的时序方差峰值可以精准定位出渗漏位置;另外,渗漏速率越大时,在高渗透通道区域处的时序方差也越大,即产生了更剧烈的自然电位异常[38].
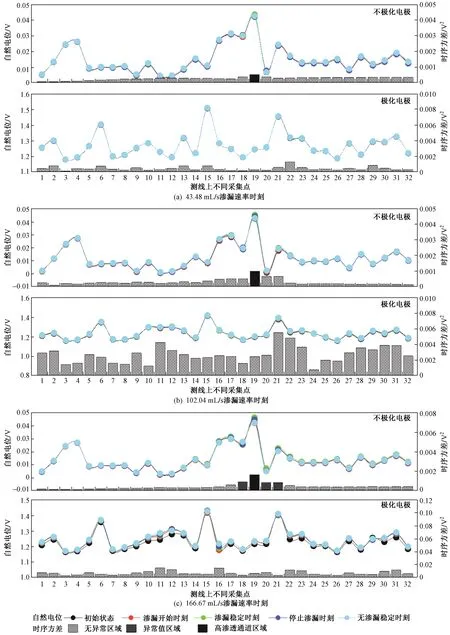
图5 不同渗漏速率下的自然电位及异常分布Fig.5 Distribution of self-potential and anomaly at different leakage rates
将不极化电极替换为极化电极后,在3种渗漏速率下,电位分布和时序方差图均不能看出明显的自然电位异常及时序方差峰值,表明极化电极并不能响应自然电位异常. 这是由于极化电极受噪声信号干扰的影响较为严重[39],且极化电极本身并不能消除极化电位,由此导致极化电极在响应自然电位异常时检测精度偏低.
2.2.2不同渗漏速率下的自然电位异常
为进一步量化分析渗漏通道处,不同渗漏速率在渗漏发生前及发展过程中不同时刻自然电位的变化,绘制了3种不同渗漏速率下的自然电位时序变化(见图6). 以图6(a)所示结果为例,在不极化电极采集条件下,在渗漏区域(19号采集点)附近,由于渗漏速率越来越大,渗滤液的流动带走高渗透性通道内表面的电荷也越来越多,因此引起的自然电位异常也更大. 在初始状态,渗漏区域(19号采集点)处的自然电位为 0.042 2 V;当渗漏速率为43.48 mL/s时,并未响应出自然电位异常;随着渗漏速率增至102.04和166.67 mL/s,渗漏区域的自然电位分别增加了 0.002 6 和 0.004 2 V,增幅分别为6.2%和9.9%. 由2.1节得出可将渗漏点近似看作一个“点电流源”的结论,则可将渗漏速率等效为“点电流源”的“电流”[36]:当渗漏速率越大时,“电流”也就越大,继而由式(2)得出响应的电位也越大.
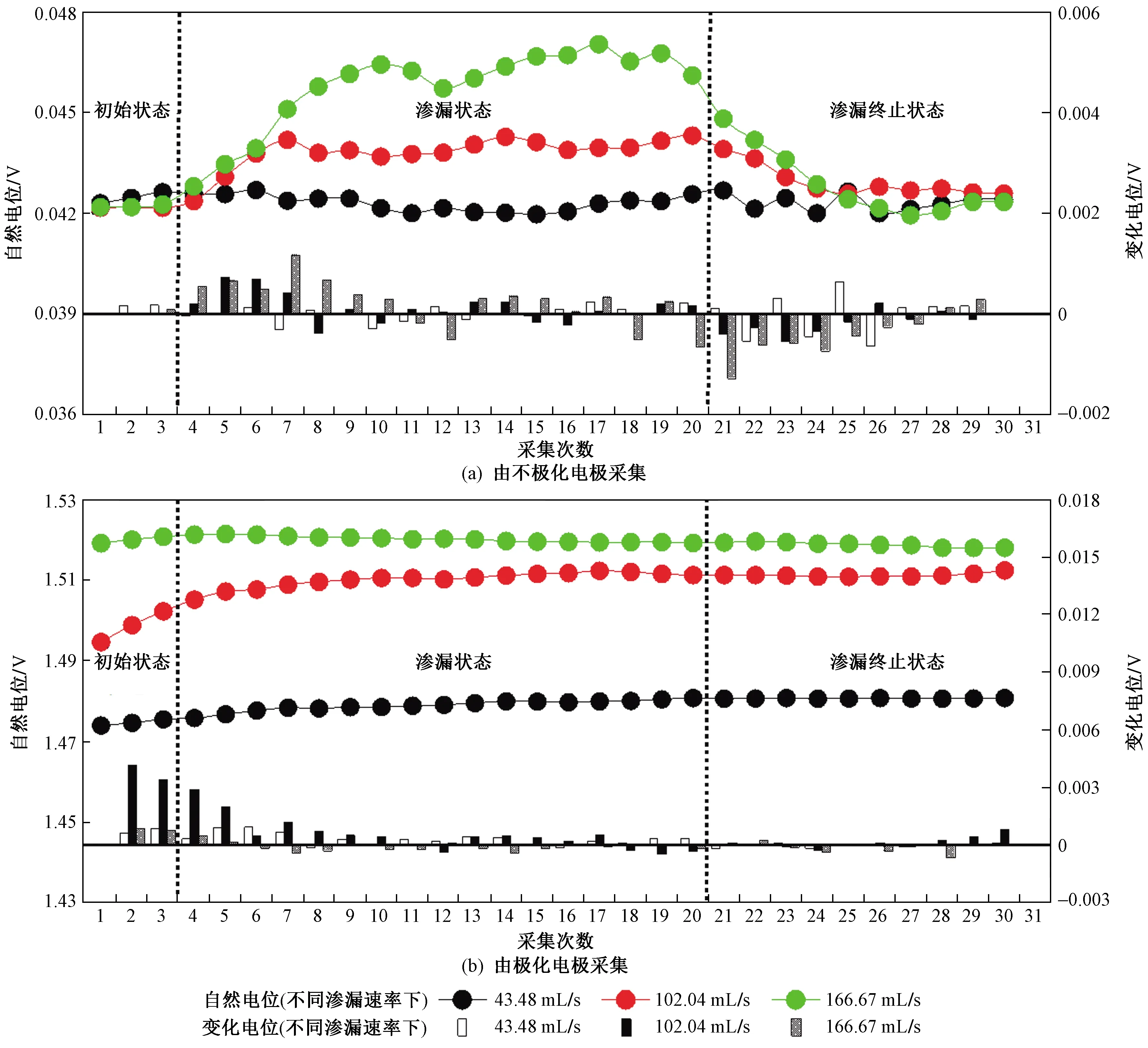
图6 不极化电极和极化电极条件下不同渗漏阶段内渗漏通道上方的自然电位特征对比Fig.6 Comparison of self-potential characteristics above the leakage channel at different leakage stages under the conditions of non-polarized and polarized electrodes
将不极化电极用极化电极替代〔见图6(b)〕,由于极化电极存在检测精度较低的劣势,导致3种不同渗漏速率条件下在渗漏区域附近并未产生明显的自然电位异常,并不能对渗漏进行响应.
结果表明,在渗漏速率大于102.04 mL/s时,不极化电极响应了 0.002 6 V的自然电位异常,且随着渗漏速率的增大,由不极化电极响应出的自然电位异常也随之增加;进一步对其进行量化分析,将渗漏点近似看作“点电流源”,则可以将渗漏速率看成“电流”,为后续对漏洞尺寸、渗漏情况进行量化研究提供一定的理论依据.
用极化电极在3种不同渗漏速率下均不能响应自然电位异常,说明不极化电极相较极化电极而言,能更好地响应低渗漏速率下的自然电位异常,具有更高的检测精度.
2.3 不同电极的对比
在一天时间内由不同电极经过两次试验检测出在渗漏区域上方(19号采集点)的自然电位时序变化如图7所示. 以图7(a)所示结果为例,在不极化电极测量条件下,在渗漏区域上方的19号采集点所检测出的自然电位值在试验初期恒定在 0.042 5 V后,随着渗漏的产生,引起了最大值为 0.004 0 V的自然电位异常. 在1 h后重复上述试验,检测到的自然电位仍保持在背景值(0.042 5 V)状态,在发生渗漏时,同样检测到的自然电位最大异常为 0.003 5 V,所产生自然电位异常的规律保持不变,自然电位异常随着渗漏的产生而增加,随着渗漏的停止而衰减.
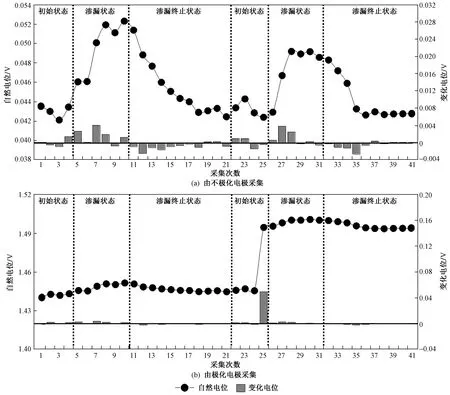
图7 一天时间所测量的自然电位及其变化Fig.7 The value of self-potential and its variation measured during one day
而当用极化电极代替不极化电极后,如图7(b)所示,在渗漏区域上方的19号采集点检测出的自然电位值在试验初期恒定在 1.442 0 V后,由于渗漏的产生引起了最大值为 0.003 0 V的自然电位异常. 但是在1 h后重复该试验时,其背景值突变至 1.494 0 V,相较之前的背景值提高了 0.052 0 V. 虽然渗漏依旧会产生自然电位异常,最大异常值为 0.003 0 V,但是其背景值发生了很大的变化. 这是因为,当有电流通过电极时发生的是不可逆的电极反应,此时的电极电位与可逆电极电位会有所不同. 电极在有电流通过时所表现的电极电位与可逆电极电位产生偏差的现象称为电极极化[40],且极化电极受到外界干扰因素(如温度、噪声等)的影响较大. 因此可以判断,不极化电极由于没有电极极化所产生的干扰因素,又具有一定的抗噪声性能,故对自然电位的检测具有更好的稳定性能.
试验结果表明,在渗漏速率大于200 mL/s时,极化电极和不极化电极均能响应自然电位异常,但是由极化电极所测量出的自然电位受电极极化、噪声等因素影响,对填埋场渗漏分析造成一定阻碍;在极化电极的基础上,不极化电极消除了电极极化效应且提高了抗噪声性能,使其更具稳定性能. 但是不极化电极制作步骤较为繁琐且结构复杂,存在造价昂贵且容易损坏的缺陷. 因此若需进行短期自然电位监测,可采取不极化电极进行精细化监测;而对填埋场进行长期稳定监测,则可通过将极化电极埋入地下来降低周围噪声对电极的干扰.
3 结论
a) 模拟典型填埋场渗漏场景和渗漏速率为200 mL/s条件下,渗漏导致自然电位异常变化可达 0.004 5 V,表明自然电位法可对渗漏进行快速响应;另外,不同位置处自然电位异常变化存在差异,其时序方差峰值与渗漏通道区域位置相吻合,且时序方差峰值达到 0.003 0 V2,与无渗漏区域时序方差(0.000 5 V2)存在明显差异,表明时序方差可以作为对渗漏点精准定位的指标.
b) 自然电位异常与渗漏速率存在显著正相关响应,在102.04、166.67、200 mL/s三种不同渗漏速率条件下,分别产生了 0.002 6、0.004 2 和 0.006 8 V的自然电位异常,即渗漏速率越大,自然电位异常越明显,表明自然电位可以对渗漏速率进行量化表征;另外,当渗漏速率减至43.48 mL/s时,自然电位无明显响应异常,表明低于该速率时自然电位法将不能对渗漏实现有效响应.
c) 在填埋场渗漏造成的自然电位异常条件下,相比于极化电极检测自然电位产生了0.052 0 V的突变,且其在渗漏速率低于166.67 mL/s时不能很好地响应自然电位异常而言,不极化电极对渗漏造成的自然电位异常变化响应更灵敏,具有更高的稳定性能和检测精度.

