成品烟箱自动装车系统垛型算法
徐跃明 方锦明 刘哲贤 郑 重 陶海旭
1红云红河烟草(集团)有限责任公司 昆明 650202 2昆船智能技术股份有限公司 昆明 650236 3清华大学精密仪器系 北京 100084
0 引言
随着物流自动化的发展,智能立体仓储和自动化分拣设备得到了广泛应用,但货车运输前的装车过程却仍然高度依赖人工,国内目前暂无成熟的自动装车系统。装货车依赖人工的主要缺点有:自动化、信息化程度低;成本高,管理难度大;效率低,很难长期保持高效率作业;缺少产品数据有效追溯;招工困难,愿意从事搬运行业的年轻人越来越少。除烟箱物流外,疫情之下的冷链物流行业对自动装车系统也有同样迫切的需求。
理论研究中把这类问题称为集装箱装载问题(CLP)。集装箱装载问题是一个经典的组合优化问题:给定一些不同规格的三维箱子,将箱子的1个子集装载进集装箱,使得集装箱的空间使用率最大。集装箱装载问题是一个NP -难的问题[1]:它是背包问题(Knapsack Problem)在三维空间上的扩展。由于背包问题本身是NP完全问题,故集装箱装载问题也不存在有多项式时间复杂度的算法。出于问题本身搜索空间的庞大,求解精确解的集装箱装载算法通常只能求解小规模的问题[2]。
Junqueira L等[3]在2012年使用混合整数线性规划模型来求解集装箱装载矩形箱的最优解,并考虑了货物稳定性和负载的约束。其使用优化软件对100多个随机生成的实例进行了全面的性能分析[4]。计算结果验证了这些模型,并表明它们只能够处理中等规模的问题。该方法的问题在于计算量过大,无法适应实际使用场景。Zhu W等[5]提出了一种分析框架来描述基于块构建的方法。该框架是基于大多数方法中存在的6个共同要素。(K1)容器中自由空间的表示;(K2)生成块的机制;(K3)用于对自由空间进行排序的启发式方法;(K4)用于对盒子进行排序的启发式方法;(K5)用于决定如何将选定的块放在选定的自由空间中的启发式方法,以及(K6)整体搜索策略。Araya I等[6]在2014年基于块构建的方法,提出了BSG-CLP搜索策略。BSG-CLP是一种基于Beam搜索的算法,其使用基于Greedy的函数来评估搜索图中的状态。Beam搜索可被看作是对分支和边界搜索的改编,在搜索图的每一层只扩展最有希望的节点的子集[7]。综上所述,针对成品烟箱自动装车系统垛型算法选择基于块构建的Beam搜索算法。
1 理论建模
针对实际烟箱码垛问题进行数学建模,并对一些限制条件进行量化。整车厢为点集A,长宽高依次为L、W、H,鹅颈板尺寸依次为a、b、c。订单顺序为集合Sj。
Sj=(li,wi,hi,nj)
式中:j为第j个订单;li,wi,hi为该品种烟箱长、宽、高;nj为数量。
操作集合为

式中:Vj,k为烟箱,1≤k≤nj;xj,k,yj,k,zj,k为左下顶点坐标。
优化目标为

下面给出了5点垛型设计数学模型中最基本的限制条件:
1)任意2个烟箱不重叠,即有

2)不同种类的烟箱尽可能依照顺序从里向外从下向上摆放,即有

3)烟箱包含在车内,即有

4)一次码放的烟箱只能在一横排上。即有

5)码放烟箱的平均时间小于阈值,即有

2 Beam Search算法
一般的搜索过程中,每一个状态都会拓展出很多个新状态,新状态又会拓展新的状态。如果采用全局搜索的方法,计算开销和状态的存储开销非常大。而采用Beam Search的算法,例如在搜索宽度是2的情况下,对初始状态拓展出2×2=4个新的状态,对这4个新状态分别做出评价,然后取评价最高的2个状态,分别各拓展出2个新状态;再对4个新状态进行评价,以此类推。因此,Beam Search的计算量远小于全局搜索,且通过调整搜索宽度又可保证一定的搜索空间,通过状态评价来尽可能地趋近较优解。Beam Search算法流程图如图1所示。

图1 Beam Search算法流程图
2.1 利用简单算法对人工码垛的复现
为了显示Beam Search算法的结果并验证其正确性,需完成1套简单的垛型仿真平台,在算法之外实现对车厢空间的还原。首先对人工码垛的思路进行复现,然后再尝试使用Beam Search等方法。
简单算法参考人工码垛时的经验,采取“码墙”的办法,即由内至外一面墙一面墙的进行码垛。具体每一面墙码放方式为:首先将相同尺寸、相同姿态的烟箱从车厢的左下角开始尽可能地放入墙中,直到不能继续放入。此时车厢右侧或上方还可能留有部分空余空间,再将该烟箱调整姿态,尽可能地放入车厢空余空间中,直到不能继续放入。如果该类烟箱仍有剩余,则开始下一面墙的码放,方式同上。如果该类烟箱在上述摆放过程中就已经放完,则开始下一品规烟箱的摆放,方式同上。依次类推,直到将车厢摆满或者烟箱被全部放入。当同一面墙中摆入了不同品规的烟箱时,其不同位置处的厚度不一样,取每面墙的最大厚度为该面墙厚度。下一面墙将从最大厚度处开始码放,故墙与墙之间可能会存在空余空间。
通过实际订单情况的检验,简单算法在设计平板车垛型时一般也能达到较高的空间利用率,且简单算法所设计出的垛型结构简单,易于装车。但由于墙与墙之间可能存在一定的空余空间(见图2),运输过程中垛型容易发生滑移甚至部分倒塌,其稳定性不够。且无法针对鹅颈板长度调整垛型设计,难以适应鹅颈板车的情况。故尝试使用Beam搜索的方式来设计垛型。

图2 简单算法垛型设计图(无鹅颈板)
2.2 Beam Search算法状态表示
搜索过程中的状态由4个基本部分组成:1)剩余箱子的集合Remaining Boxes,即还有哪些箱子需要被放入车厢;2)空余空间的集合 Empty Spaces,即还有哪些地方可以放箱子;3)当前可选的烟箱块Available Blocks;4)已经码放完成的箱子顺序和位置的记录Moves。最难表示的是空余空间集合。
如图3所示,把1个立方体放入空的立方体空间后,剩余的空间是不规则的立体图形。使用重叠的长方体集合(Empty Maximum Spaces):对每个箱子,以其1个面为分界面,向空的方向最大延伸的长方体。如图3a中的空余空间可由图3b~图3d中3个透明空间表示。

图3 Empty Maximum Spaces示意
具体到算法中,图4中的紫色透明长方体就是从已经码放好的箱子的面上向外延伸的最大的空长方体。
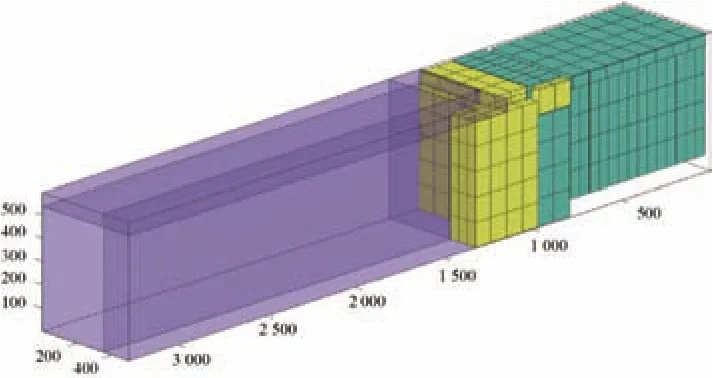
图4 实际状态中的剩余空间表示
2.3 Beam Search算法状态拓展
简单来说,搜索过程中的状态转移过程是搭积木的过程,每次选择1个空余空间、选择由多个箱子组成的Block,然后将Block放入空余空间中并更新状态。
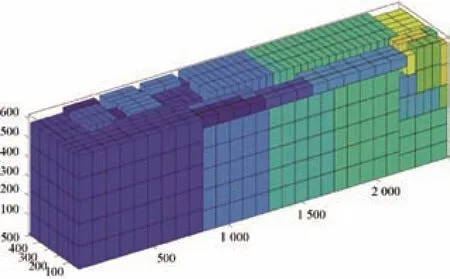
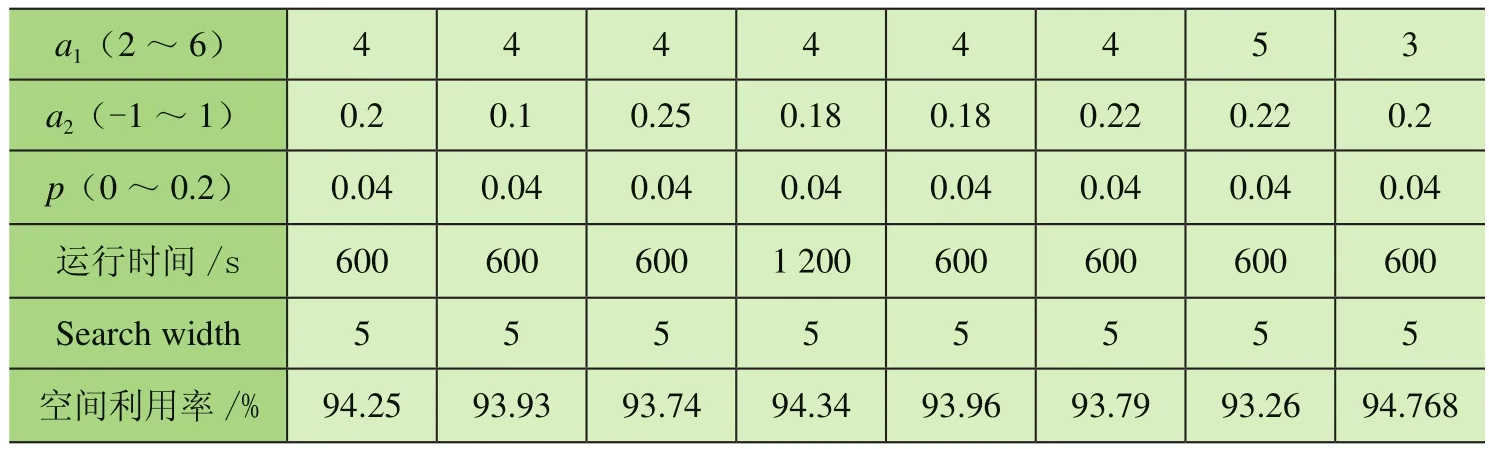
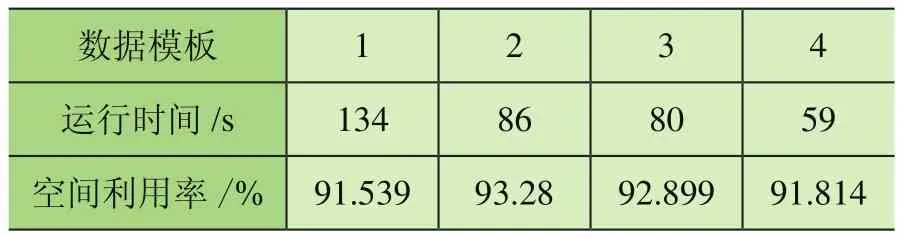
在选择空余空间时采用加权曼哈顿距离对可选空间进行评价排序,取出优先级最高的空间。加权曼哈顿距离为:distance=w_1X+Z+w_2Y;其中,w_1 在选定待放入烟箱和空余空间后需要对状态进行更新。从剩余箱子的集合中减去Block包含的箱子,从空余空间集合中删掉放入箱子的空间,并加入新产生的空间,其中需要处理空间相互包含的情况,同时如果前面选择了空余空间后遍历所有块都无法放入,则删除该空间,如果烟箱块需要的烟箱数量大于剩余烟箱,则在可选的烟箱块集合中删除该块,最后在Moves中记录下这步操作,完成状态拓展过程。 在Beam Search的过程中,每拓展一些新状态,就要对新状态进行一次评价,以挑选出当前认为最好的几个状态。采用的评价过程为:使用贪心算法来得到完整解,即从当前状态出发进行搜索宽度为1的搜索,不断拓展状态直到车厢被放满。然后使用该完整解的空间利用率作为当前状态的评价。 该方法可在搜索算法全部完成前就先得到完整解,多数情况贪心算法得到的完整解效果也能满足实际需求。 在设计完成垛型后,算法还需指导自动装车完成码垛工作,故需根据垛型来反推不同位置烟箱的码放顺序与位置。码放顺序原则为: 原则1:烟箱1左下坐标(x1,y1,z1),烟箱2左下坐标(x2,y2,z2)。若x1<x2,则烟箱1先于烟箱2码放;若x1=x2,z1<z2,则烟箱1先于烟箱2码放;若x1=x2,z1=z2,y1<y2,则烟箱1先于烟箱2码放。 原则2:放入某个烟箱时,该烟箱下底面与其他烟箱或车厢底面的接触面积之和应大于下底面面积的90%; 原则1保证了已放入的烟箱不会对机械装置发生干涉,原则2保证了装入的烟箱具有足够的支撑。此外,由于自动装车的设计为每次可放入1排若干个烟箱,为了提高装车效率,应尽可能每次将处在同一排的烟箱一起放入。算法流程如下: 1)先将垛型中所有烟箱按照原则1排定摆放顺序,从先到后编号为1~N; 2)i=1~N,依次考虑第i个烟箱时,依据原则2判断能否放入,若不能放入则进入等待序列;若能放入则进入摆放序列,并将等待序列中重新满足原则2的烟箱进入摆放序列。 上述流程可满足摆放要求,但会出现处于同一层的可一次性放入的烟箱顺序被分散在摆放序列中。为了提高效率,在上述流程的第二步中,加入重新考虑等待序列的前提条件:当自动装车恰好可以一次性放入其能力极限的烟箱个数时,再考虑等待序列中的烟箱能否进入摆放序列。 2.6.1 系统输入 系统输入为装有烟箱订单数据的Excel表格,如表1所示。 表1 订单数据表 2.6.2 系统输出 根据车辆有无鹅颈板及订单中烟箱总量是否超出单车装载能力,系统的输出可分为多种情况。图5~图8展示的4种垛型效果图为:车辆无鹅颈板且订单中烟箱总量超出单车装载能力;车辆有鹅颈板且订单中烟箱总量超出单车装载能力;车辆无鹅颈板且订单中烟箱总量小于单车装载能力;车辆有鹅颈板且同品规烟箱集中放置。 图5 垛型效果图(无鹅颈板、订单中烟箱总量超出单车装载能力) 图5最外侧大长方体代表1个车厢,单个小立方体代表单个烟箱,同种颜色的小立方体代表同一订单中同一品规的烟箱,图6中左下角深蓝色部分和图8中右下角白色部分代表车辆鹅颈板。当订单中烟箱总量超出单车装载能力时,系统会以车厢空间利用率尽可能高为目标进行垛型设计。当订单中烟箱总量低于单车装载能力时,系统会在保证订单中烟箱全部装入车厢的基础上考虑垛型在运输过程中的稳定性,如图7所示。 图6 垛型效果图(有鹅颈板、订单中烟箱总量超出单车装载能力) 图7 垛型效果图(无鹅颈板、订单中烟箱总量小于单车装载能力) 图8 垛型效果图(有鹅颈板、同品规集中放置) 系统的评价函数中有许多超参数,例如评价过程中各影响部分的权重值,需要通过实验确定其最佳取值。 表2和表3为评价函数中各参量不同取值对实验结果的影响。其中a1为相邻面积权重,a2为单个Block中烟箱个数权重,p为计算相邻面积时的距离系数,Search width为搜索宽度。 表2 参数取值对结果的影响 表3 参数取值对结果的影响 从实验结果中可知,当a1=3,a2=0.04,p=0.04时,相同情况下车厢的空间利用率最高。 对于不同的订单数据,程序运行结果呈现出一定的差异性,总体来看,程序对不同订单输入都有较好的效果,能满足实际需求。从表2和表3可知,程序在不同数据输入的情况下运行240 s左右设计出的垛型能达到92.5%以上的空间利用率。同时根据实际需求,一般要求装车垛型至少达到90%的空间利用率,通过表4和表5可知,程序在不同数据输入的情况下最长需要134 s达到该标准,对于某些特定订单只需60 s左右即可满足要求。表6展示了当空间利用率要求提高至93%时程序对于不同订单数据所需要的运行时间。 表4 程序在相同参数下对不同订单数据运行240 s左右结果(有鹅颈板) 表5 程序在对不同订单数据达到90%空间利用率所需最短时间(有鹅颈板) 表6 程序对不同订单数据达到93%空间利用率所需最短时间(有鹅颈板) 图9和图10依次展示了程序在不同搜索宽度下的垛型空间利用率随时间变化曲线和程序对于不同订单输入下的垛型空间利用率随时间变化曲线。 图9 无鹅颈板不同搜索宽度下空间利用率随时间变化曲线 图10 不同订单数据空间利用率随时间变化曲线 由图可知,不同搜索宽度下程序运行结果存在较大差异,当Search width取值大于3时总体效果较好。同时对于不同订单信息输入,程序的运行结果也存在一定的差异,但都能够满足90%空间利用率以上。 基于Beam Search算法建立成品烟箱自动装车系统算法的数学模型,通过简单算法的仿真平台显示Beam Search算法的结果并验证其正确性。通过参数测试得出当a1=3,a2=0.04,p=0.04时,相同情况下车厢的空间利用率最高。通过系统稳定性测试得出,不同搜索宽度下程序运行结果存在较大差异,当Search width取值大于3时总体效果较好。同时对于不同订单信息输入,程序的运行结果也存在一定的差异,但都能够满足90%空间利用率以上。2.4 Beam Search算法状态评价
2.5 垛型反推摆放顺序
2.6 研究结果分析




3 参数测试与系统稳定性测试
3.1 系统参数测试

3.2 系统稳定性测试




4 结论

