新课改下高中数学教学的对策

陈腾云

20世纪末，国家就已经提出革新教学体制、推进素质教育、全面培养学生的要求，开展了新课程标准改革，主要目的就是要在21世纪构建起全面、系统化、以素质教育为教学任务的现代基础教育体系，以素质教育为核心培养全面发展的高素质学生。为了符合新课改的教学要求，高中数学教师需要不断深化自己的教学认知，以创新的方式和手段来提高教学质量，在教学过程中充分呈现对学生的素质提升和能力培养。

一、融入知识背景

高中数学知识体系庞杂，许多公式理论都晦涩难懂。在教学过程中，如果教师只是一味地向学生灌输生硬的知识，就会使得很多学生无法快速入门，甚至有小部分学生会彻底放弃数学。为了改变这样的情况，教师的教学活动也需要进行调整，如让学生参与探究活动，让学生知其然，也知其所以然，在理论推导过程中深化学生的理解。这虽然有益于提升学生的认知水平，但也是不全面的教学，未能让学生看到数学的全貌。教师除了教知识本身和推导过程，还要让学生认识到数学知识的相关历史背景。

以“集合”的教学为例，在传统的教学中，教师基本上是通过各种案例的共同点来让学生学习集合的概念，顺着集合的定义来讲述集合的元素、集合的多种表达方式等内容。在这样的教学活动中，学生只是对“集合”的相关知识进行了表层的学习。在一定程度上，这些内容学生仅仅通过自学的方式也能掌握，或是只需要教师花费很少的教学时间。所以，教师可以充分利用空闲时间，对教学内容进行拓展，让学生学习到数学理论的历史背景。教师可以在教材知识讲授清楚之后，再给学生简要地叙述“集合”的历史由来：古代人面对复杂繁多的事物，产生了分类整理的想法，之后这一想法逐渐应用在数学学科中，直到19世纪60年代，德国著名的数学家康托尔看到了集合在数学基础知识中的广泛应用，于是开始系统地整理有关集合的知识。通过向学生讲述“集合”的历史背景，有助于学生对相关知识有更深的理解和把握，从而提升学生主动学习数学知识的兴致。

二、渗透思想方法

数学思想是学生在数学学科教学活动中需要培养的思维能力，有助于学生熟练地解决各种数学实际问题。学生常常会遇到各种难以解决的数学问题，在一定程度上，这并不是因为学生对知识的掌握不牢靠，而是学生对数学思想、数学方法不能随心所欲地运用。在传统教学实践中，高中数学教师很少会关注数学思想方法在课堂上的渗透，认为数学学科的学习与解决数学难题能力的掌握是一致的，让学生一味地刷题，最后事倍功半。因此，教师应该注重在教学课堂上向学生渗透各种数学思想，使学生的思维更加活跃、视野更加开阔。

以“圆的方程”一课教学为例，在推导圆的方程公式时，教师首先构造了一个平面直角坐标系，接着将一个半径为一个单位的圆放入坐标系中，通过两点之间距离的计算公式以及圆心点的坐标，最终得出了圆的方程式。在之前的教学中，教师往往在推导出这一公式后便戛然而止，事实上，在圆的方程公式推导过程中，充分体现了“数形结合”“函数与方程”的数学思想，教师不能仅仅停留在知识的表面，更要在传授知识的过程中，让学生认知到数学理论的推导也运用了各种各样的数学思想。教师可以单独用一节课的时间，讲述数学思想和数学方法的运用，提高学生的解题能力，鼓励学生对数学思想和方法善加利用，不断增加学生学习数学学科的兴趣。

三、建立思维框架

高中数学知识是分散而凌乱的。在过去，教师的教学活动基本上死板地按照教材目录进行，被教材牵着鼻子走，导致学生所掌握的数学知识也是不成体系的。有的直到学生开始进行数学整体知识的复习活动时，也无法构建数学知识的整体框架。因此，教师应该积极引导学生构建知识框架结构，提高学生的学习效率和对知识的掌握程度。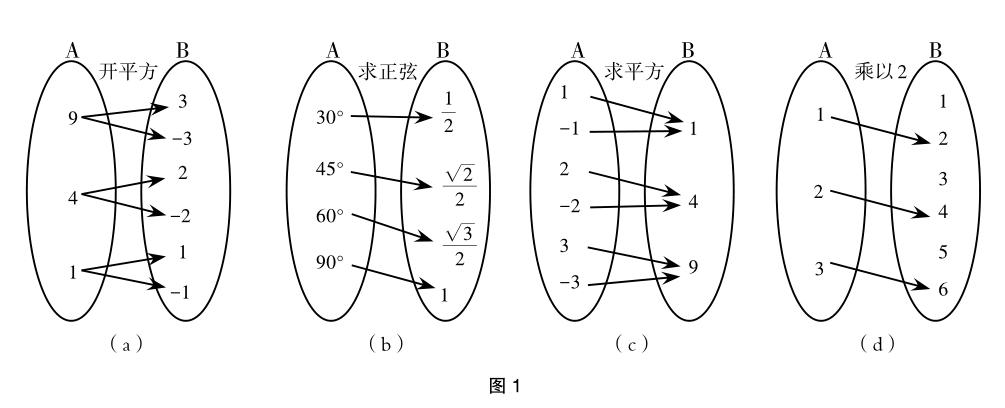

例如，选修一“曲线方程”的知识是对必修二的相关数学内容的承接，在教师完成全部的教学任务之后，可以再利用一整节课的时间，引导学生对这些内容进行梳理和把握。首先，教师可以让学生重新回顾有关“直线与方程”“圆与方程”“圆锥曲线与方程”三部分的内容，仔细研读教材并总结它们的相似点。接着教师以“曲线方程”为大标题，以“直线”“圆”“椭圆”“双曲线”与“抛物线”为二级标题制作知识框架，将它们的方程公式、基本性质等基础内容全部直观地呈现出来，使学生有关于“曲线方程”的知识变得更加系统化、体系化，学生对这些知识的理解和应用能力也会大大提升。

四、引导自主探究

在长期应试教育的影响下，很多学生已经习惯了“知识来伸手，题来思考”，被动接受知识，缺少了自主探究的意识和能力，这导致学生对数学知识思考的深度不够。有的教师为了提升学生的学习成绩和节约时间，会选择性地给学生讲述数学知识，导致学生越来越依靠教师的教学，没有主动性，造成了学习效率低下。因此，教师可以作为一个引导者的角色去指导学生自己学习和思考数学知识，提升学生自主探究的能力。

例如，在教学“函数”相关内容的时候，其中第一课时的教学目标是让学生了解映射和一一映射的概念，以便学生更为深入地了解函数的概念。这一目标完全可以通过自主探究的方式去实现。教师可以给出学生之前接触过的关于“对应”的例子，如看电影的时候，电影票需要和座位实现一一对应；在数轴上一个实数和唯一的一个点是对应的；在坐标上面有一个点是和一个有序对相对应的……让学生思考这是什么原则，学生给出答案——这是一一对应原则。之后，教师给学生展示图片（图1），要求学生思考并找到对应的原则。学生思考之后给出答案——从左边的角度说，有的是一对多，有的是一对一，有的是多对一。至此，学生能找出如何对应的形式。之后引导学生总结映射的概念。教师只需要引导学生说出符号即可。

五、联系生活实际

生活中處处是数学。著名教育家和思想家陶行知先生提出“生活即教育”的理念。从目前教学的现实条件出发，教师不可能随时随地跟着学生，在生活中指导他们学习，但是可以将教学与生活相联系，实现生活化教学。一方面可以增强学生的学习兴趣，另一方面也可以引导学生深入理解数学知识，大大帮助学生提升自身的数学素养。

例如，在教授“抛物线方程”相关内容的时候，教师可以利用多媒体给学生播放江南水乡美景的视频，其中拱桥的设计充分体现了劳动人民的智慧。观看视频可以让学生身临其境，充分认识到学习抛物线的价值和意义，更有动力去展开学习。老师还可以设计关于拱桥的问题，在给学生展现的拱桥美景中，教师可以标注这个拱桥的跨度是30m，高是5m，让学生求出这个对应的抛物线方程。这样巧妙结合生活实际的方式增强了课堂的生动性，让学生更加有动力去解决问题。在这一过程中，教师可以和学生探讨为什么要这样设计桥，有什么好处，最为重要的是还能让学生感受我国古代人民的智慧，领略祖国的美景，激发学生的爱国情怀。

总之，新课程标准改革对高中数学教师开展教学活动提出了新的要求。当下的教育更加注重学生能力与素养的提升，更加强调学生参与教学活动的主体意识。因此，教师应该不断更新自己的教学观念，改进各种教学手段，思索“与时俱进”的、更适合学生全面发展的教学策略，充分发挥学生在教学活动中的主体性，开阔学生的视野和拓展学生的思维，让学生深入领略高中数学的无限魅力。