基于ADAMS螺旋伞齿啮合力的动态仿真分析

李光志

（长春汽车工业高等专科学校，吉林 长春 130011）

推土机用途广泛，能在多种复杂、恶劣的环境中作业，是一种非常理想的高效型施工机械。在实际的使用过程中，中央传动中的螺旋伞齿轮出现了裂纹、断齿现象，存在一定的危险后果，因此有必要对这对螺旋伞齿在工作过程中所承受的啮合力进行分析研究。

传统的设计中，通常考虑在某种恒力的作用下来分析齿轮在啮合过程中所承受中载荷，主要是静力学上的研究，而齿轮在实际啮合过程中是存在冲击和振动现象的，齿轮力在啮合过程中也将是变化的。针对直齿和斜齿的力学分析，国内外学者做了很多研究，提出了参数在动态啮合过程中的选取方法等，本文针对某型推土机驱动桥中央传动的螺旋伞齿轮，进行动态仿真分析研究，来获取轮齿在工作过程中啮合力的变化规律，为螺旋伞齿轮的进一步设计提供相关的参考依据。

1 模型的建立

某型推土机的中央传动是由一对螺旋圆柱齿轮、一对螺旋伞齿轮等零件组成。其中动力通过与小螺旋伞齿轮同轴的圆柱齿轮传递过来，小螺旋伞齿轮为主动齿轮，大螺旋伞齿轮与之啮合为被动齿轮。其传动简图如图1所示。

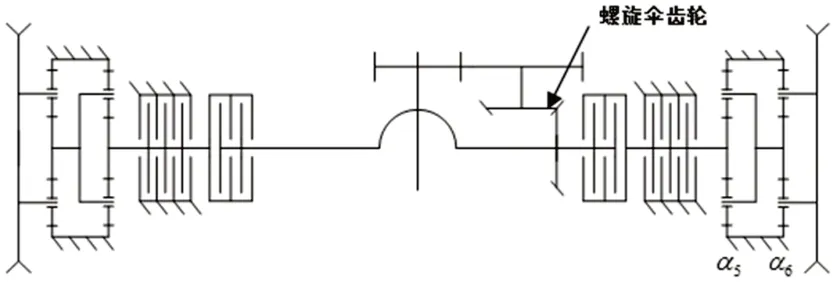
图1 中央传动的传动简图

本文基于三维建模软件Proe来创建中央传动的三维模型。将三维模型以x-t文件格式导入到adams中，对螺旋伞齿轮参数重新进行定义、并施加约束。这对螺旋伞齿轮的主要的基本参数如表1所示。

表1 螺旋伞齿轮主要的基本参数

2 仿真条件的设定

以经典Hertz接触理论为依据，可得到两刚体之间相接触时其接触刚度的计算公式如下：

式中，R为综合曲率半径；δ为分锥角。

齿轮轮齿的啮合冲击所引起的啮合力，可以看作两个圆柱体撞击接触问题。将这对螺旋伞齿轮的相应参数带入到上述公式，得到刚度系数K：

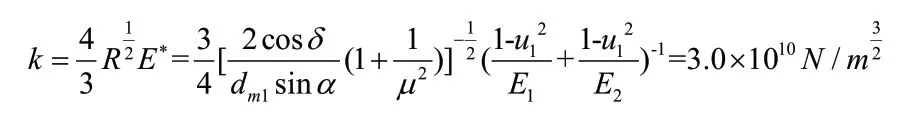
3 理论与仿真结果分析

3.1 负载相同，不同角速度下螺旋伞齿啮合力分析

在被动螺旋伞齿轮的质心处施加反向转矩100N·m，让其承受一定的阻力，在这里使用step函数使负载在1s内平缓作用(图2)，即step(time，0，0，1，100)，避免施加负载时出现陡变现象。在主动螺旋伞齿轮的质心处添加Ar/min的角速度来驱动：工况1时A=30；工况2时A=60；工况3时A=100。用step(time，0，0，，1，6A d)使速度在1s内均匀加速，以工况1为例，如图3所示。

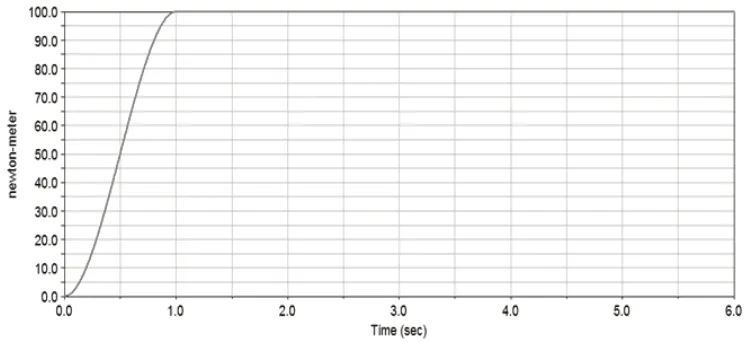
图2 转矩负载图

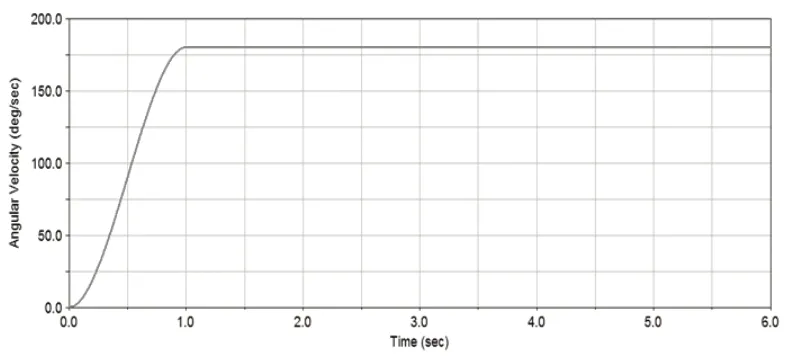
图3 转速驱动图

对3种工况分别进行仿真，其被动螺旋伞齿轮角速度仿真结果如图4所示。

图中自上而下第三条、第二条以及第一条曲线分别为工况1、工况2和工况3时所对应的被动齿轮角速度变化曲线。从图4中可以看出，在啮合传动过程中齿轮的角速度均在一个均值附近以一定的幅值上下波动，波动幅度随着角速度的增加而增大。其主要参数如表2所示。

表2 齿轮角速度变化主要参数

图4 齿轮角速度变化曲线

表中，ωm为角速度平均值；ωmax为角速度最大值；ωmin为角速度最小值。

对3种工况分别进行仿真，螺旋伞齿轮所受的切向分量啮合力F仿真结果如图5所示。

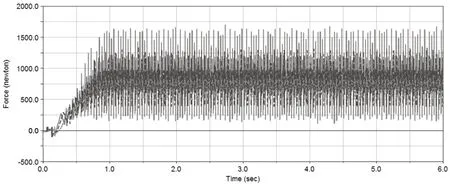
图5 齿轮切向分量啮合力变化曲线

从图5中可以看出，螺旋伞齿轮在开始啮合的瞬间，存在较大的波动，说明开始时啮合过程中受到了较大的冲击；在啮合传动过程中螺旋伞齿轮也存在较明显的冲击振动，啮合力均在一个均值附近以一定幅值进行上下波动，也存有动载成分。其主要参数的数值分析见表3所示。

注浆全部完成后，剪切锚索外露端，余留长度不大于60 mm，混凝土铺底，厚度100 mm，强度等级C30。

表3 切向啮合力变化主要参数

表中，Fm为啮合力平均值；Fmax为啮合力最大值；Fmin为啮合力最小值；λ1为啮合力最大值与平均值之比；λ2为啮合力最小值与平均值之比；

从表3可以看出，传动速度越大，齿轮啮合力动载幅值越大；齿轮的动载荷也并非是对称循环的，其动载荷的均值大于静载荷。

将ω11=30r/min，ω12=60r/min，ω13=100r/min

分别代入得：

ω21=21.9r/min；ω22=42.58r/min；ω23=70.97r/min

螺旋伞齿切向力理论计算：

理论计算值与仿真值的数值分析如表4所示，其中的误差值是仿真值与理论计算值的差值与理论计算值的比。

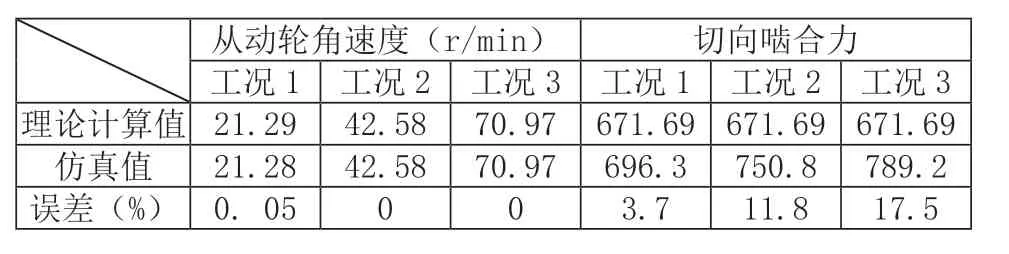
表4 螺旋伞齿角速度、切向啮合力的仿真值与理论值的比较

从表4中可以看出，从动轮角速度的仿真值与理论值的误差很小，可以忽略不计，近似认为角速度的仿真值与理论值一样；而啮合力的仿真值与理论值误差较大，正说明齿轮在啮合过程中存在较大的动载，当角速度越大时冲击和振动强度越大螺旋伞齿轮所承受的啮合力越大。

3.2 角速度相同，不同负载下螺旋伞齿啮合力分析

在主动螺旋伞齿轮的质心处添加30r/min的角速度来驱动。在被动螺旋伞齿轮的质心处施加反向转矩T，工况1时T=100；工况2时T=500；工况3时T=2000。

对3种工况分别进行仿真，其被动螺旋伞齿轮x向啮合力大小数值分析见表5所示。

表5 X向啮合力分析

理论计算：

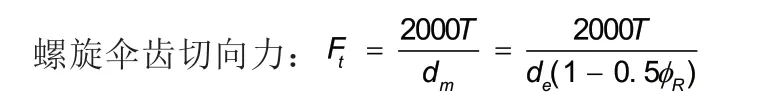
螺旋伞齿X向啮合力：

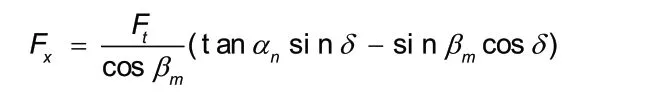
将工况1时T=100；工况2时T=500；工况3时T=2000，分别代入得：

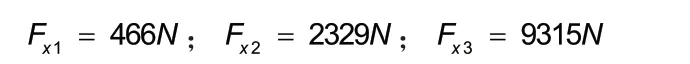
理论计算值与仿真值的数值分析如表6所示，其中的误差值是仿真值与理论计算值的差值与理论计算值的比。

从表6中可以看出，螺旋伞齿X向啮合力的仿真值与理论值误差较大，同样也说明齿轮在啮合过程中存在较大的动载，会有冲击和振动。

表6 螺旋伞齿X向啮合力仿真值与理论值的比较

4 结语

本文针对推土机中央传动中的一对螺旋伞齿轮进行研究。利用adams仿真软件进行动力学仿真，在不同工况下齿轮啮合力的变化情况，并与理论计算数值进行对比，指出其变化是一种以定值为中心的近似对称循环的波动，当齿轮的角速度越大时其啮合力也将越大，理论值与仿真值间的误差越大，螺旋伞齿在啮合过程中的动载越大；当螺旋伞齿所受的负载变化时，其X向啮合力的仿真值与理论值也存在较大误差，也说明在啮合过程中有冲击和振动现象。通过研究齿轮传动过程中动态啮合力的变化情况，为螺旋伞齿的设计使用提供一定的参考依据。