求解大型稀疏线性方程组的加权拟极小残差算法
陈晓花
(兰州财经大学 陇桥学院,甘肃 兰州 730101)
0 引言
对于大规模线性稀疏系统
Ax=b
(1)
其中A∈Rn×n是稀疏且非奇异矩阵,x,b(∈Rn)为n维向量,其求解近年来倾向于运用迭代法.在众多迭代法中,目前最为活跃和有发展前途的方法是Krylov子空间方法.而Krylov子空间中有两类方法应用比较广泛,一类是基于Arnoldi过程构造Krylov子空间
Km(A,r0)=span(r0,Ar0,…,Am-1r0)
(2)
的正交基的方法,如目前应用最多的GMRES(Generalized minimum residual method)算法[1],FOM算法等,对这类算法的研究也是目前国内外研究的热点,如Azeddine Essai在文献[2]中提出了一种称为Weighted GMRES的方法,利用加权技术加快了GMRES算法的收敛速度;另一类是基于Lanczos双正交化过程产生Krylov子空间
Km(A,v1)=span(v1,Av1,…,Am-1v1)
(3)
和
Km(AT,ω1)=span{ω1,ATω,…,(AT)m-1ω1}
(4)
的算法,如QMR(Quassi Minimal Residual)算法[3],BiCG(Bi-orthogonal Conjugate Gradient)算法,BiCGSTAB算法等.本文结合文献[2]中的加权思想,对QMR算法进行了改进,即得到了WeightedQMR算法.数值试验表明,对某些问题该算法的收敛速度优于QMR算法.
1 Lanczos双正交过程
算法1 Lanczos双正交过程[3]
(1)选取两个向量v1,w1,使得(v1,w1)=1.
(2)令β1=δ1≡0,w0=v0≡0.
(3)Forj=1,2,…,m,Do:
(4)αj=(Avj,wj)
(11)EndDo.
构造三对角矩阵Tm如下:
令Vm=[v1,…,vm],Wm=[w1,…,wm],则有如下的命题成立:
命题1[3]如果上述算法1在m步之前不会发生中断,则{vi}(i=1,2,…,m)和{wi}(i=1,2,…,m)分别是子空间:
Km(A,v1)=span(v1,Av1,…,Am-1v1)
(5)
和Km(AT,ω1)=span{ω1,ATω,…,(AT)m-1ω1}的基,向量{vi}(i=1,2,…,m)与{wi}(i=1,2,…,m)满足关系式(vj,wi)=0,i≠j,1≤i,j≤m,(vi,wi)=1,1≤i≤m且有如下的等式成立:
(6)
(7)
(8)
2 加权QMR算法


2.1 加权Lanczos双D-正交过程
下面利用上述D-内积的定义,给出加权的Lanczos双D-正交化过程.
算法2 Lanczos双D-正交过程

(3)Forj=1,2,…,m,Do:

(11)EndDo.



(9)
其中

(10)

(11)




(12)

(13)
若i =0 (14) (15) 算法3 WQMR算法 算例1 本例中矩阵取自矩阵市场(http://math.nist.gov/MatrixMarket/),条件数为3.5319e+004,非零元素个数为2423,阶数为153,其结构如图1所示,其迭代次数与残差图如图2所示: 图1 算例1矩阵结构图 图2 迭代次数与残差图 算例2 矩阵结构如下: A=01-10⋱⋱⋱1-10æèççççöø÷÷÷÷100×100,迭代次数与残差如图3:图3 迭代次数与残差如图 算例3 矩阵结构如下: A=1111-111⋱⋱-1⋱⋱⋱1⋱⋱⋱1⋱⋱1-11æèçççççççöø÷÷÷÷÷÷÷300×300,计算结果如图4:图4 计算结果比较 算例4 系数矩阵为如下三对角矩阵: A=3-2-13-2⋱⋱⋱⋱⋱-2-13æèççççççöø÷÷÷÷÷÷200×200迭代次数与残差图如图5:图5 迭代次数与残差图 利用D-内积改进Lanczos双正交过程,得到加权的Lanczos双D-正交过程,进而得到加权拟极小残差算法(WQMR),数值算例表明,对于某些带状矩阵,该算法是有效的,且收敛性优于QMR算法.但该算法的优越性很大程度上是依赖于权值d,对给定的矩阵A,如何选取最优的权值d,目前还在研究当中.

2.2 加权拟极小残差算法(WQMR)

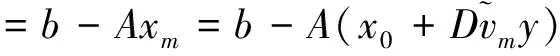

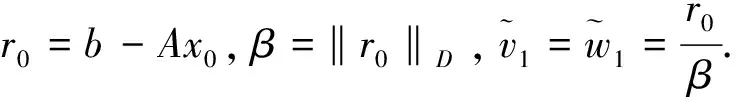



3 数值算例

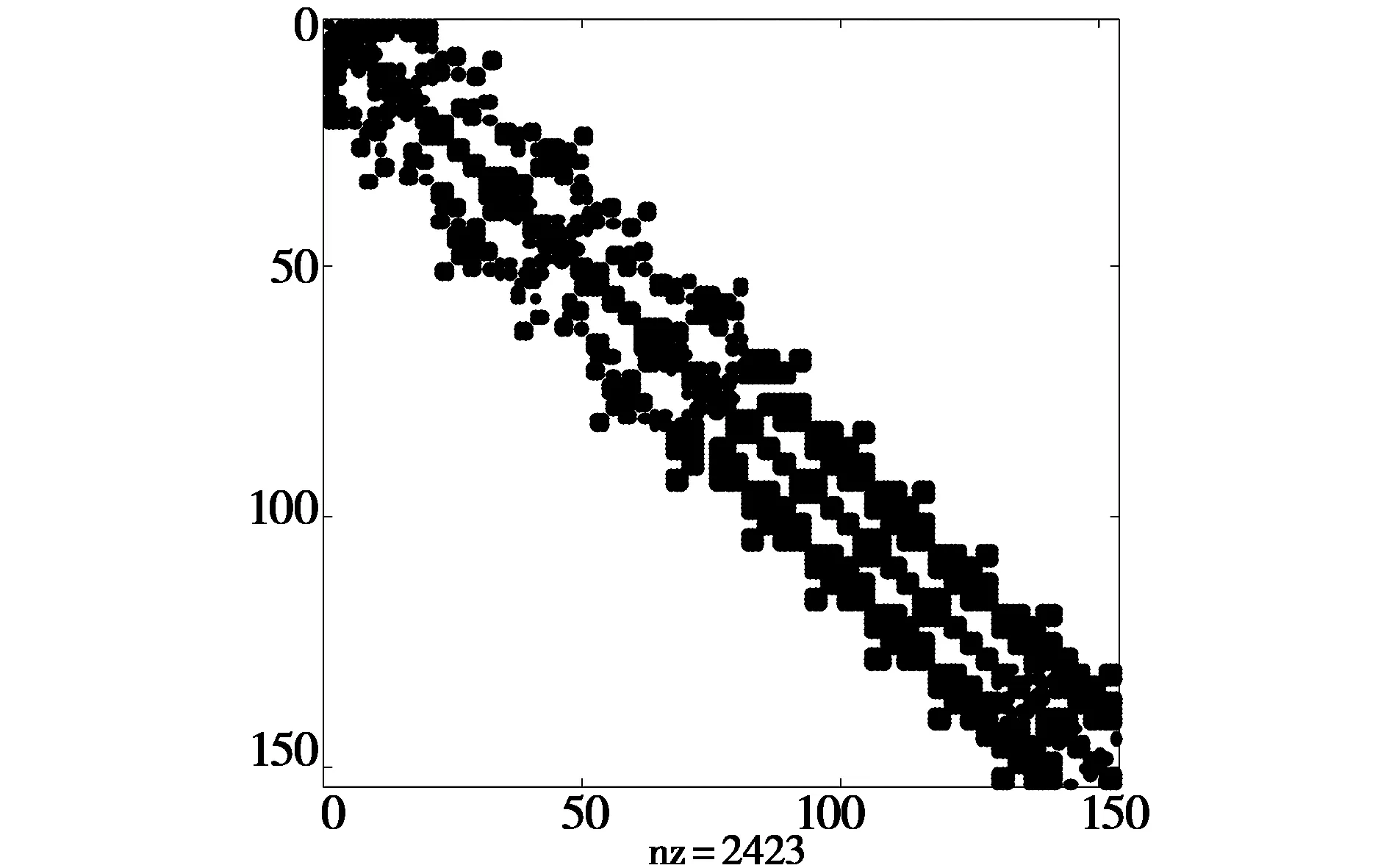




4 结论

