应用(Φ/Ψ)展开法求广义Zakharov方程组的精确解

何彩霞

(青海师范大学 民族师范学院院物理系，青海 西宁 810008)

0 引言

广义Zakharov方程组(generalized Zakharov equations，以下简称GZEs)是描述高频波与低频波相互作用的典型非线性偏微分演化模型，在等离子体物理，非线性光学等领域具有广泛的应用.一维无量纲形式如下[1，2]：

(1)

λ是常数，该方程考虑了等离子体的自生磁场效应，即含λ的项.若λ=0，方程组(1)便是著名的等离子体Langmuir波湍流方程[3].其中i2=-1，E=E(x，t)是复数，表示高频电场强度的慢变振幅的包络波解，n=n(x，t)是实数，表示离子数密度偏差.近年来，随着非线性方程求解方法的不断发展，求GZEs的精确解已涌现出多种有效方法，如：扩展F-展开法[4]，exp-函数法[5]，变分迭代法[6-8]，第一积分法[9]，辅助常微分方程法[10]，Jacobi椭圆函数法[11]，分岔方法[12]，Painlevé展开法[13]，直接代数法[14]等.然而，寻找新形式的精确解仍然是一件很有意义的工作，如在等离子体物理方面非常有利于研究等离子体波的性质.

王明亮等人[15]提出的(G'/G)展开法是求解非线性方程精确解行之有效的方法，被广泛地应用和推广，在近期的工作中，人们对此方法做了进一步的改进和拓展，如：扩展的(G'/G)展开法[16]，(G'/G2)展开法[17]，(G'/G，1/G)扩展法[18]，(Φ/Ψ)展开法[19]等.本文应用(Φ/Ψ)展开法求得了GZEs的丰富精确解.这种方法快速、简明、有效.

1 (Φ/Ψ)展开法

非线性偏微分演化方程

H(u，ut，ux，utt，uxt，uxx，…)=0，

(2)

其中u=u(x，t)是未知函数，H是u及u关于x，t各阶偏导数的多项式.应用(Φ/Ψ)展开法求解该方程的主要思想如下：

步骤1 做行波变换

u(x，t)=u(ξ)，ξ=Kx-Ωt+ξ0，

(3)

其中K，Ω为待定常数.经(3)变换，(2)就转化为含行波变量的常微分方程：

H(u，u′，u″，…)=0，

(4)

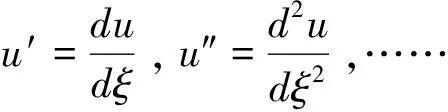
步骤2 将方程(4)的解表示为(Φ/Ψ)的多项式

(5)

其中ai为待定常数，正整数m由齐次平衡法确定，Φ(ξ)，Ψ(ξ)满足

Φ′(ξ)=βΨ(ξ)，Ψ′(ξ)=αΦ(ξ)，

(6)

即满足

(7)

β，α均为待定常数.

步骤3 将方程(5)代入常微分方程(4)，结合方程(7)合并(Φ/Ψ)的相同幂次项，令(Φ/Ψ)的各次幂的系数为零，得到关于变量ai(i=1，2，3，…，m)，α，β的非线性代数方程组.

步骤4 求解步骤3中的非线性方程组，得到ai(i=1，2，3，…，m)的解.

步骤5 将步骤4中的各解和(6)式的解代入(5)式，即可求得常微分方程(4)的多个精确解.

方程(6)的解有如下几种形式：

Ⅰ 当α>0，β>0时，

Ⅱ 当α<0，β<0时，

Ⅲ 当α<0，β>0时，

Ⅳ 当α>0，β<0时，

上述C1和C2式是常数.

2 Zakharov方程组的精确解

首先，对广义Zakharov方程组(1)做变换

E(x，t)=eiηφ(ξ)，n(x，t)=n(ξ)，

(7)

ξ=Kx-Ωt+ξ0，η=kx-ωt+η0，

(8)

其中，K，Ω，ξ0，k，ω，η0是待定常数.将(7)(8)式代入方程组(1)可得下列两式

-i(Ω-2Kk)φ′+(ω-k2)φ+K2φ″-2λφ3+2nφ=0，

(9)

(Ω2-K2)n″-2K2(φ′2+φφ″)=0，

(10)

分离(9)式中的实部与虚部.令虚部为零，得Ω=2Kk，实部为

(ω-k2)φ+K2φ″-2λφ3+2nφ=0，

(11)

GZEs转化为非线性常微分方程组(10)和(11).由齐次平衡法可确定φ，n的幂次分别为m1=1，m2=2.因此，可设上述方程组解的形式如下：

φ=a-1(Φ/Ψ)-1+a0+a1(Φ/Ψ)，

(12)

n=b-2(Φ/Ψ)-2+b-1(Φ/Ψ)-1+b0+b1(Φ/Ψ)+b2(Φ/Ψ)2，

(13)

其中a-1，a0，a1，b-2，b-1，b0，b1，b2是常数.

将(12)和(13)式代入(10)和(11)，结合(7)合并(Φ/Ψ)的同次幂的系数，再令这些系数为零，得到关于a-1，a0，a1，b-2，b-1，b0，b1，b2的非线性代数方程组，解这些非线性代数方程组得：

(14)

(15)

(16)

(17)

Ⅰ 当α>0，β>0时，

(18)

(19)

其中ξ=Kx-Ωt+ξ0，Ω=2Kk，η=kx-ωt+η0.

Ⅱ 当α<0，β<0时，

(20)

(21)

其中ξ=Kx-Ωt+ξ0，Ω=2Kk，η=kx-ωt+η0.

Ⅲ 当α<0，β>0时，

(22)

(23)

其中ξ=Kx-Ωt+ξ0，Ω=2Kk，η=kx-ωt+η0.

Ⅳ 当α>0，β<0时，

(24)

(25)

其中ξ=Kx-Ωt+ξ0，Ω=2Kk，η=kx-ωt+η0.

同理，对(14)，(15)，(17)式，分别结合(12)—(13)代入(7)，可得到GZEs的另外十二组精确解.

3 讨论与总结

(26)

(27)

(28)

(29)

若取C1>0，C2=0，(18)和(19)式可变成下列形式

(30)

(31)

同理，依次可分析另外十五组解的简单形式.

与扩展F-展开法[4]和He变分法[8]相比较，我们用(Φ/Ψ)展开法得到了广义Zakharov方程组的丰富双曲余切函数解.选取适当的参量，可清晰地刻画出波的传播情况，研究等离子体的自生磁场效应、振荡频率、波数等不同参量对等离子体波的传播特性的影响.这一方法将进一步用于获得量子Zakharov方程组的精确解，研究量子效应对等离子体波传播的影响.此方法也可用于求解其它非线性演化方程的精确解.