直径为3的单圈图的极小Hosoya指标
刘巧云,吴廷增
(青海民族大学 数学与统计学院,西宁 810007)
自Hosoya[1]提出这一拓扑指标以来, 很多学者都研究过Hosoya指标[2-6]. 本文基于Hosoya指标定义, 提出和计算了直径为3的n阶单圈图的Hosoya指标计算公式并得到了具有最小、次小的Hosoya指标的极图, 并由此得到直径为3的n阶单圈图的Hosoya指标排序.
1 预备知识
本文仅考虑无向简单图.记图G(V,E), 其中V代表图的顶点集合,E代表图的边集合.具有n个顶点,m条边的图记为G(n,m)图.当n=m且n≥3时, 这一类图G(n,n)称为单圈图.
对于两个顶点u和v(u≠v),u和v之间的距离是u和v之间最短路的边数.一个图的直径是G中任意两点间距离的最大值.

定义1[1]图G的Hosoya指标计算式为:

其中:p(G,k)为G中选择k条两两不相连的边数的方法,t是G中选择k条两两不相连的边的最大数.对任意图G(n,m),p(G,0)=1,p(G,1)=m.


2 直径为3的单圈图的最小Hosoya指标

下面我们分别讨论Ui(i=1,2,3,4)中的具有最小Hosoya指标的图需要满足的条件.
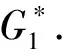

图1 长度为3的四种单圈图 Fgure 1 The four unicycle graphs with diameter 3


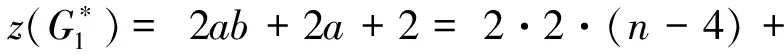









case 2:若a+b<3, 只能取a+b=2, 但是G2需满足a+b+c=n,a≥1,b≥1,c≥1,且a,b,c中至少有两个大于等于2,即a+b≥3.产生矛盾.此种情况不可能出现.


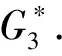

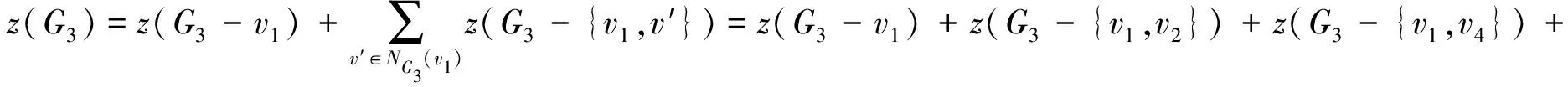


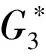
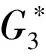




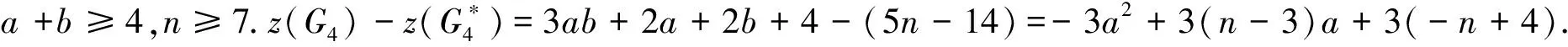
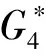
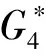
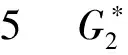
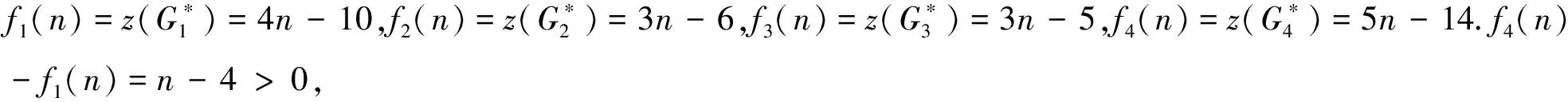
综上所述,当n≥6时,f2(n) case 1:若a<3(即a=2)或b<2(即b=1)时,此时Hosoya指标最小. 证明设G2∈U2, 且1≤a≤b≤c.利用定理2, 有z(G2)=abc+a+b+c. case 1:若a+b<4, 即a+b=3,此时Hosoya指标最小. case 2:若a<2, 即a=1时,Hosoya指标最小. case 1:若a<2(即a=1)时,Hosoya指标最小. g4(n)-g1(n)=(8n-32)-(6n-22)=2n-10>0,从而g4(n)>g1(n).g1(n)-g3(n)=(6n-22)-(5n-15)=n-7>0, 从而g1(n)>g3(n).g3(n)-g2(n)=(5n-15)-(4n-12)=n-3>0, 从而g3(n)>g2(n). 综上所述, 当n≥7时,g2(n) 研究有n个顶点的直径为3的单圈图Ui(i=1,2,3,4)的Hosoya指标排序问题.记z(G1)=h1(a,b),z(G2)=h2(a,b),z(G3)=h3(a,b),z(G4)=h4(a,b). 定理12U2的Hosoya指标排序情况: 本文得到了直径为3的n阶单圈图的Hosoya指标计算公式并得到了具有最小、次小的Hosoya指标的极图, 并由此得到直径为3的n阶单圈图的Hosoya指标排序. 今后可以继续研究直径更大的情况下的Hosoya指标与实际应用问题.
3 直径为3的单圈图的次小Hosoya指标
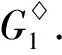


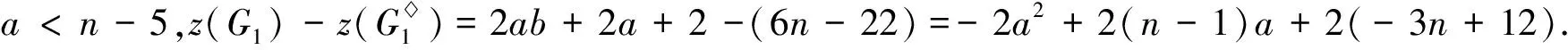





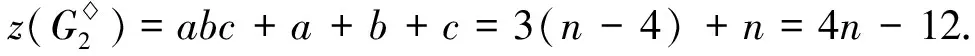













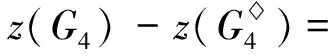
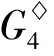
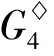
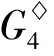

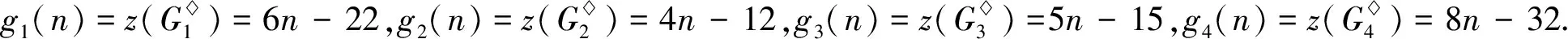

4 Hosoya指标排序
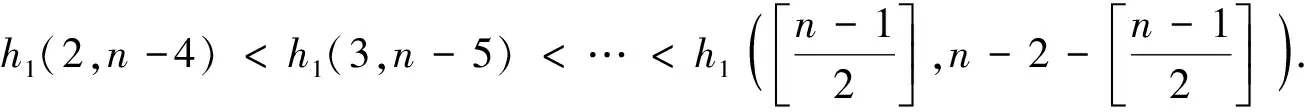







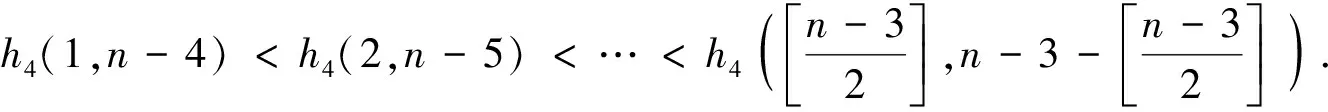
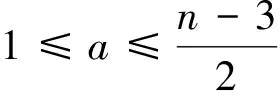
5 结 语

