基于惯性动力系统的加速梯度算法

李 春 凯

(北京邮电大学 理学院， 北京 100876)

近年来，优化算法广泛应用于机器学习领域，对于求解大规模的问题，Hessian矩阵的计算和存储成本大，因此一阶梯度算法再一次回归主流.对连续时间下的常微分方程(Ordinary differential equation，ODE)与离散迭代算法建立联系，获取加速梯度算法引起越来越多的关注.

本文针对二阶的ODE 采用不同的离散格式，得到了加速梯度算法.

1 研究方法

本文考虑无约束最优化问题：

(1)

其中：f是光滑的凸函数.最基础的一阶梯度算法是梯度下降法(Gradient decent method，GD):

xk+1=xk-sf(xk),

(2)

其中:x0是初始点，s是步长.在一阶优化算法的框架下，是否存在改进GD收敛速率的算法是一个微妙而重要的问题.

1.1 动量方法

动量方法是指迭代过程中在仅使用一阶梯度信息的基础上加入前一步的迭代信息的一种方法.现代对于这种扩展的一阶算法的研究可以追溯到Polyak[1-2]，他在GD 的基础上加入动量项(xk-xk-1)，得到重球方法(Heavy-Ball):

yk+1=xk-sf(xk)，xk+1=yk+1-α(xk-xk-1)(3)

其中:α>0是动量系数.重球方法在最小值附近比GD能获得更快的局部收敛速率，但它通常并不能保证全局加速.而且Lessard[3]证明了即使对于强凸函数，由于步长的选择，重球方法并不能保证收敛性.

另外一种重要的动量方法是Nesterov[4-5]提出的Nesterov加速梯度算法(Nesterov’s accelerated gradient algorithm，NAG),当目标函数f为强凸函数时，迭代形式为：

(4)

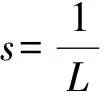
(5)

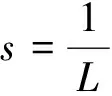
1.2 连续时间ODE

近年来，通过连续时间的ODE来分析加速梯度算法越来越受到人们的关注.特别是Su等人[6]表明，假设目标函数f为凸函数，当s→0时，NAG可收敛到一个关于时间t的连续时间ODE:

(6)

Su等人通过构造合适的连续时间下的Lyapunov函数，证明了在连续时间下迭代点的加速收敛速率，进而佐证NAG具有加速收敛速率.

文献[7-8]中Lagrangian和Hamiltonian框架被用来生成一大类连续时间的ODE，以便统一处理基于加速梯度的方法.但Wilson等人指出[8]，当f为强凸函数时，NAG对应的ODE为:

(7)

重球方法对应的ODE与式(7)相同，然而重球方法和NAG的迭代形式并不一样，NAG的收敛速率更快且收敛性更好，因此并不能通过分析式(7)体现出NAG的优势.因此Shi等人[9]在计算ODE过程中提高精度，得到重球方法和NAG的高精度的ODE.值得注意的是，当f为强凸函数时，重球方法和NAG的高精度ODE是不同的，分别为：

(8)

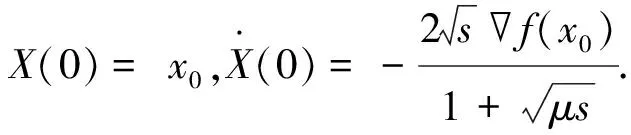
(9)

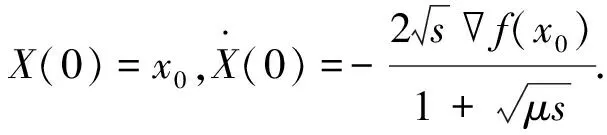
1.3 离散化ODE

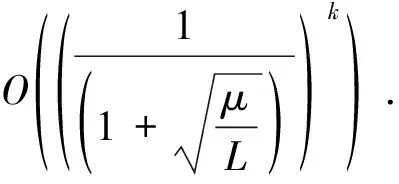
2 惯性动力系统

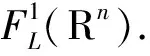
‖f(y)-f(x)‖≤L‖y-x‖

当目标函数f为强凸函数时，重球方法对应的高精度ODE(8)和NAG对应的高精度ODE(9)都可以看作是Attouch文中[14]中特殊形式的Hessian-driven惯性动力系统:

(10)

对该连续时间系统离散化，可以得到一系列的优化算法.系统中包含的Hessian项可以看作是f(X(t))对t的导数，正好对应到NAG中函数梯度差.

在优化问题中，Polyak[12]首先利用惯性动力学使梯度法获得加速收敛速率，即带有摩擦系数的连续时间下的重球方法(HBF)：

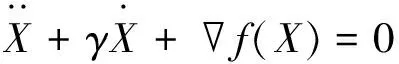
(11)

其中：阻尼系数γ>0，由于很难取到合适的γ，且在一些优化问题中，收敛性并不好.Alvare[15]受连续时间牛顿方法启发，引入Hessian项，得到类牛顿的惯性动力系统(Dynamic inertial system，(DIN)γ,β)：

(12)

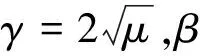
(13)

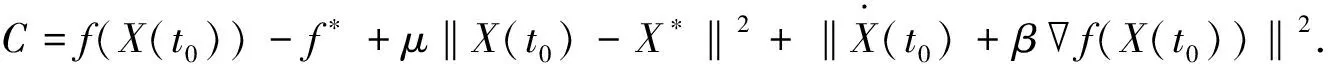
本文的目的是通过不同的离散格式对式(13)离散化，得到优化算法，并证明定理1中的指数收敛速率可转换为离散迭代格式下的线性收敛速率.

3 新的优化算法

采用三种离散格式：辛格式，显示Euler，隐式Euler对上述微分方程离散化，得到三种优化算法.

3.1 辛格式优化算法

第一种离散格式是辛格式，近似规则如下:

由辛格式离散ODE(13)可得优化算法：

证明设Lyapunov函数为：

已知

f(xk+1)-f(xk)≤〈f(xk+1),xk+1-xk〉-

2x*)+vk+1+vk+β(f(xk+1)+f(xk))〉-

2x*)+vk+1+vk+β(f(xk+1)+f(xk))〉-

2x*)+vk+1+vk+β(f(xk+1)+f(xk))〉-

已知以下两个等式

和

显然成立，所以

因为目标函数为强凸函数，所以满足

因此可得：

由假设可知

根据强凸性质

所以

由Cauchy-Schwarz不等式，可知

βf(xk)‖2≤

成立.所以

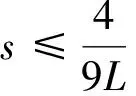
3.2 显式Euler优化算法

第二种离散格式是显式Euler格式，近似规则如下:

由显式Euler格式离散ODE(13)可得优化算法：

证明设Lyapunov函数为：

βf(xk)‖2+f(xk)-f(x*)

<1)，且各件产品是否为不合格品相互独立．

vk+1+vk+β(f(xk+1)+f(xk))〉≤

根据Cauchy-Schwarz不等式以及f为强凸函数，以下两个不等式

和

成立，因此

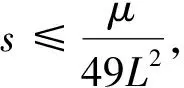
利用Cauchy-Schwarz不等式得：

x*‖2+‖vk‖2+β2‖f(xk)‖2)

又因为f为强凸函数，所以有：

因此

3.3 隐式Euler优化算法

另一种格式是隐式Euler格式，近似规则如下：

2f(xk+1)vk+1≈f(xk+1)-f(xk)

由隐式Euler格式离散ODE(13)可得优化算法：

证明设Lyapunov函数为：

βf(xk)‖2+f(xk)-f(x*)

vk+1+vk+β(f(xk+1+f(xk))〉≤

根据Cauchy-Schwarz不等式

3μ‖xk+1-x*‖2+f(xk+1)-f(x*)

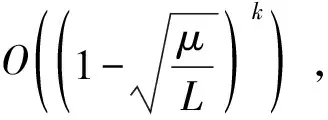
4 结 语

本文主要是通过离散连续时间下的惯性动力系统得到加速梯度算法.具体是通过三种不同的离散格式：辛格式、显式Euler和隐式Euler对该动力系统进行离散后得到三种优化算法，并证明了当目标函数是强凸函数时，由辛格式以及隐式Euler离散惯性动力系统(13)得到的的优化算法能够实现与文献[13]中相同的加速收敛速率.