Ka频段宽带步进频ISAR成像仿真

卢奎锋，段 锐，李 沫，张 健*

（1.电子科技大学电子科学与工程学院，四川成都 611731；2.电子科技大学信息与通信工程学院，四川成都 611731）

雷达进行目标探测的距离分辨率与发射信号带宽呈正相关。用于提高雷达分辨率的技术有超宽带雷达技术、超分辨技术、脉内脉冲压缩技术和脉间脉冲压缩技术等。超宽带雷达技术通过发射极窄的无载波脉冲实现高距离分辨力，需要具有较大瞬时带宽的模拟-数字转换器对回波信号进行采集，并且所需的宽带收发器件也区别于传统窄带雷达。超分辨技术主要采用高分辨力的最优估计算法实现，这类方法利用了接收信号协方差矩阵中的统计特征，如使用多频段雷达谱外推实现超分辨［1］。脉内脉冲压缩技术是一种常用的提高雷达距离分辨力的方法，通过对每个发射脉冲进行脉冲频率编码或相位编码以提高系统的瞬时带宽。步进频率雷达采用的是一种脉间压缩方法，其连续发射脉冲的载频按照固定的频率步进量变化，大带宽利用多个子脉冲信号处理后间接实现。

常见的成像雷达，多利用脉内脉冲压缩技术，发射脉内调制瞬时大带宽信号，接收机采用去斜接收架构，混频得到相对而言带宽窄的目标回波信号，降低了信号处理端数据采集的压力。但如果采用相控阵体制，受孔径渡越效应的制约，大带宽、大天线口径波束扫描时会出现波束偏移，一方面会造成波束指向误差影响角度分辨，另一方面会对宽带回波信号带来幅度调制，影响纵向目标一维距离像［1］。为了消除孔径渡越效应的影响，需要采用延时线进行延时补偿，从而面临在目标距离分辨率、角度分辨率、复杂度之间做权衡。尤其是对于毫米波相控阵雷达，阵元间距很小，该问题十分严重，甚至会导致无法实现宽带大孔径相控阵雷达。

步进频率法的主要优点是相对于其他提高距离分辨力的方法，它仍然维持了较低的瞬时信号带宽。从常规脉冲多普勒相控阵雷达系统的成像能力系统改造而言，只需要增加步进频率宽带合成信号处理器以及步进频率成像模式下对应的时序和波形。更重要的是，对于大孔径的空间目标探测相控阵雷达系统而言，步进频率雷达发射的瞬时窄带信号，在宽角扫描时，可以轻松避免大口径宽带相控阵天线带来的孔径渡越效应。

虽然美国林肯实验室分别于2010 年和2014 年研制出带宽分别为4GHz 和8GHz 的毫米波成像雷达［2］，但它采用的是大孔径抛物面天线，不是相控阵雷达。本文针对Ka频段大孔径毫米波宽带相控阵成像雷达，首先分析了孔径渡越效应对波形带宽设计的限制。然后设计了合成带宽5GHz 的步进频率波形，并基于逆合成孔径雷达（Inverse Synthetic Aperture Radar，ISAR）成像转台模型，对空间目标模型进行了ISAR 成像仿真，以验证波形参数的成像能力。

1 步进频率雷达系统

典型的步进频率雷达系统主要特征为具有发射信号中心频率可快速跳变的频率综合器，以及相对应的可将目标回波信号合成为等效宽带波形的信号处理模块。图1 为步进频率信号典型收发时序关系，发射频点和接收频点的跳变关系，图2 为步进频率体制雷达基本组成架构［3］。

图1 步进频信号时序示意图Fig.1 Stepped frequency radar timer

图2 步进频雷达原理框图Fig.2 Stepped Frequency Radar Block Diagram

步进频率雷达系统关键参数包括：子脉冲个数N，子脉冲带宽BW，脉冲宽度Tp，相邻步进频率脉冲间隔Δf。常规雷达脉冲波形，如：简单脉冲信号、线性调频信号、二相编码信号等都可以用于步进频雷达系统中。对于子脉冲为简单脉冲的步进频信号而言，一般认为脉冲带宽BW与脉冲宽度Tp之间关系为BW= 1/Tp。线性调频波形脉冲宽度和信号带宽之间不存在反比的约束关系，可独立设计。线性调频信号调频斜率K=BW/Tp，宽带处理后合成带宽B=BW+ (N- 1) · Δf。

对于脉冲重复频率间隔（Pulse Repetition Interval，PRI）为Tr的系统，设雷达位置为坐标原点，点目标与雷达相距R0处，则目标回波模型为

其中，fn为第n个子脉冲的中心频率，假设f0表示第一个子脉冲的中心频率，则

简单脉冲基带信号s1的表达式为

子脉冲信号粗分辨率ΔR′ =c/(2BW)，宽带合成处理后分辨率ΔR=c/(2B)。

对采用移相器产生扫描波束的宽带相控阵雷达，当信号频率f偏离中心频率f0为Δf，即f=f0+ Δf时，天线的方向图F(θ)为

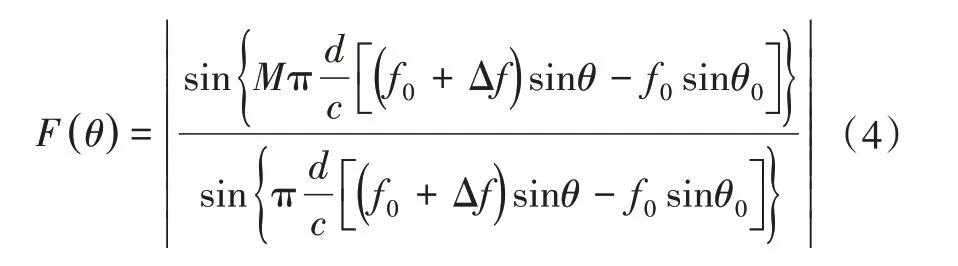
其中，c为光速，θ0为天线波束扫描起始角度，θ为波束扫描指向角度。

当阵元间距d=c/(2f0)，利用阵面尺寸L=Md代替阵元数M进行估算。假设阵列天线口径为6 m，参考频率为35 GHz 的Ka 波段毫米波相控阵天线，带宽为5 GHz，当扫描角度达到电扫天线常规限定值60°时，40 GHz 信号下波束实际指向约为50. 3°。限定带宽的合理准则为当极限扫描角为60°时，可容忍的最大波束偏移角不超过中心频率波束宽度的±1/4［4］，利用阵列天线方向图计算公式，在设计步进频率雷达子脉冲带宽时，在宽角扫描极限下，瞬时带宽不应超过的极限值为20 MHz。

2 步进频ISAR成像模型

转台模型是ISAR 成像最直观的模型。以雷达所在位置为参考原点，定义散射点旋转中心坐标，以及散射点坐标。成像模拟时，已知转台模型中目标相对于旋转中心旋转角速率为ω，以及在以雷达O为原点的坐标系中目标散射点的初始时刻位置，基于此条件可迭代计算散射点在采样时刻t的坐标以及相对于雷达的径向距离和径向速度，通过计算目标实时距离和实时速度就可以得到模拟目标散射点回波的延时和多普勒频移。从而可以得到模拟目标回波数据用于ISAR成像“仿真”。

以目标旋转中心O为参考建立局部坐标轴xOy，假设目标单个散射点P坐标为P(x，y)，目标旋转中心相对雷达距离矢量为R，散射点P与雷达间距离矢量为Rp，目标回波形式可表示为

其中，目标ρ(x，y)为散射点反射密度函数，散射点P 的坐标随时间变化，与雷达径向距离为Rp(t)，则

图3 转台模型Fig.3 Turntable model

其中，R(t)为目标旋转中心相对于雷达的径向距离。

设目标绕旋转中心旋转角速率为ω，角加速度为γ，则

由此，目标回波可表示为

利用τ= 2x/c，以及fd= 2fωy/c代入（9），得

从上式可以看出，回波信号是距离和多普勒频率的函数［5］，如果对转台模型回波信号SR(t，f)做逆傅里叶变换，可得到与目标散射点坐标相关联的目标反射密度函数，即

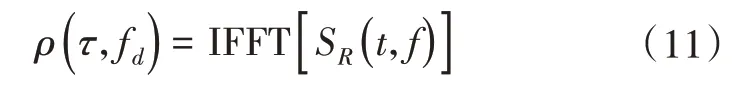
该函数直接与目标坐标(x，y)相关，包含目标的二维特征。结合步进频率雷达信号特征，基于步进频体制的目标ISAR成像回波模型为

其中，θ(tk，i，m)表示第m帧、第i个频率下，tk采样时刻目标旋转角度，即

其中tk∈[ 0，Tr)，i∈[ 1，N]，m∈[ 1，M]。M为步进频率信号帧数（完整的连续N个步进频率变频为一帧），其取值影响多普勒频率分辨率。

由此，基于步进频率信号的ISAR 成像仿真程序中，每个PRT回波采集一个样本点，然后对单帧的N个步进频率子脉冲回波做逆傅里叶变换，得到快时间维（距离维）高分辨一维距离像，对不同帧的同一频点的M个采样点做FFT变换，得到慢时间维（速度维）像，由于不同散射点不同位置速度矢量不同，由此将相同径向距离的目标分离开来，得到距离-多普勒（Range-Doppler）二维图像，可反映目标的外形特征。

3 ISAR成像仿真

步进频率雷达工作于成像模式，引导设备提供的目标初始距离仅影响发射机和接收机本振频率之间的延时，在此模式下，雷达多工作在高重频参数条件下，距离高度模糊，以确保速度无模糊。考虑到系统探测距离和分辨率指标，为了实现5 GHz的合成带宽，在满足大口径电扫描相控阵列天线瞬时带宽的约束前提下，设定步进频率间隔为10 MHz，则步进频率数为500。在设计波形时兼顾距离模糊度和数据率要求，脉冲重频设定为50 μs。 成像系统仿真参数如表1所示。

表1 ISAR成像系统仿真参数Tab.1 Simple pulse waveform simulation parameter

根据所设仿真参数，可得到ISAR 成像性能列表（表2）。

表2 ISAR成像系统性能参数Tab.2 Simple pulse waveform performance parameter

纵向无模糊距离窗和横向无模糊距离窗大小限定了成像目标的最大尺寸，即仿真目标尺寸大小约束在15 m×15 m范围之内。

利用目标模型坐标生成步进频率回波信号，对回波信号做二维IFFT 变换，得到转台模型下ISAR 成像结果。原始目标尺寸为1. 9 m×3. 8 m，从成像结果可以看出，目标成像位于窗口中心，目标形状特征明显，未发生明显的目标折叠现象，所设计的波形参数具有一定的实用价值（图4-7）。

图4 目标散射点分布Fig.4 Target scatter position

图5 目标纵向高分辨像Fig.5 High resolution range profile of the target

4 结论

图6 目标横向高分辨像Fig.6 High resolution cross range profile of the target

图7 ISAR二维成像结果Fig.7 ISAR two-dimension imaging result

大口径宽带毫米波成像雷达由于孔径渡越效应的限制，瞬时带宽受限。首先基于孔径渡越效应得到步进频率雷达瞬时带宽的最高限制，利用ISAR成像转台模型，将步进频率雷达体制与之相结合，推导了目标回波模拟信号产生公式，对所提出的宽带波形参数通过ISAR 成像仿真，得到特征明显的二维成像结果，验证了步进频率宽带雷达体制的高分辨特性。