噪声相关系统中估计误差方差奇异的滤波融合算法

杨钰晗，李 智，牛顿标，宋恩彬*

（1.四川大学数学学院，成都 610065；2.电子信息控制重点实验室，成都 610063）

R.E.Kalman于1960年提出Kalman滤波［1］，自此Kalman滤波便在目标跟踪、遥感、导航定位、战场监视、制造过程监控和复杂机械状态维护等实际领域［2］有着广泛的应用。然而单个传感器的Kalman滤波难以满足高精度和高容错性等要求［3］，而多传感器Kalman滤波融合接收信息更全面，能适应不同的环境变化，获得更准确的估计值，因此在众多领域得到广泛的应用，并逐渐成为研究的热点。

多传感器系统的滤波融合方式主要有中心式融合与分布式融合两种。分布式融合相比中心式融合，虽然信息量有一定的损失，但计算量小、通信负担低、网络结构灵活、可靠性高，是目前应用最为广泛的信息处理方法。所以，使信息损失达到最小，甚至等价于中心式融合的分布式Kalman滤波融合算法受到了越来越多的关注。

文献［4］-［6］提出了经典分布式Kalman滤波最优融合算法，并证明了该分布式算法融合结果与中心式Kalman滤波等价，使得分布式Kalman滤波融合既具有分布式系统的众多优点，又具有与中心式Kalman滤波一样优良的滤波性能。然而在实际应用中，由于连续系统离散化，系统或信号处于同一噪声源污染的环境以及模型转化等原因，各传感器之间的观测噪声往往是相关的，由此而形成的噪声相关系统得到广泛研究。例如，文献［7］针对这类系统，提出了与中心式等价的一类融合算法。文献［8］通过对测量值和相关参数进行线性变换，使传感器噪声相关性解耦，实现与中心式等价的估计性能。此外，在有些随机动态系统中，状态向量可能会受到各种约束［9］，例如，车辆在固定道路中移动，钟摆沿圆周进行摆动等。这些系统固有的约束信息限制了目标状态的运动轨迹，同时导致融合过程中实际的过程噪声方差是不可逆的，估计误差方差阵也是奇异的。文献［10］针对带有不等式约束线性系统提出了一类无味Kalman滤波算法；文献［2］和文献［11］针对估计误差方差是奇异的动态系统提出了一类融合算法，其估计性能与中心式的融合算法一致，解决了这类问题。

但在实际应用中，多传感器线性估计系统复杂多样，可能出现估计误差方差是奇异的噪声相关系统，而上文提及的融合算法都只针对解决其中一类问题，无法适用于两种问题同时存在的情况。本文针对这类特殊系统，提出了一个基于最优加权矩阵的融合算法，该算法放宽了已有算法对系统的观测噪声和过程噪声的限制，即允许：（a）观测噪声方差阵和过程噪声是奇异的；（b）不同传感器之间的观测噪声是相关的。最后通过模拟仿真，将本文所提出的融合算法与中心式融合算法和文献［2］中对应算法进行对比分析，比较三种算法的估计误差，数值结果验证了所提融合算法的有效性。

1 问题描述

1.1 系统描述

本文考虑由l个传感器构成的离散分布式动态系统，即

其中，F k∈R n×n为状态转移矩阵，H ik∈R li×n为第i个传感器的状态观测矩阵，vk，xk∈R n分别为k时刻的状态与过程噪声，yik，wik∈R li分别为第i个传感器k时刻的观测向量和观测噪声。为方便后文描述，可将l个传感器的观测组合起来，得到联合的观测方程，即

其中，yk=(y1k'，…，ylk')'，H k=(H1k'，…，Hlk')'和wk=(w1k'，…，wlk')'。

1.2 过程噪声和观测噪声统计特性描述

对于不同的时刻k，过程噪声与观测噪声wik为不相关的零均值高斯随机变量，但当i≠j时，因本文考虑不同传感器的观测噪声wik与wjk在同一时刻k存在相关性，所以联合的观测噪声方差阵为R k=cov(wk)，该矩阵第(i，j)块为，可以为非零阵。其中主对角块为第i个传感器的观测噪声方差阵过程噪声协方差矩阵为Q k=cov(vk)∈R n×n，由于本文放宽了对噪声方差的限制，所以只需求Q k是一个半定阵。

1.3 经典Kalman滤波

根据文献［12］中经典Kalman滤波的结果，利用所有传感器观测的中心式滤波迭代式，即

其中，(·)†表示矩阵的伪逆（Moore-Penrose逆），也称广义逆。为方便下文融合算法的描述与公式推导，类似中心式滤波的迭代，可得到第i个局部传感器的滤波迭代式，即

1.4 问题难点

因本文考虑同时存在噪声相关和估计误差方差阵奇异的系统，所以其分布式融合存在两个难点。第一，因为各传感器的观测噪声具有相关性，所以观测噪声协方差矩阵R k不是对角块的，无法利用文献［2］的方法，通过对R k进行分块直接得到分布式的融合算法。第二，因为过程噪声协方差矩阵是奇异阵，估计误差协方差矩阵也是奇异的，而文献［9］所提融合算法需要用到上述两个矩阵的逆矩阵，所以无法利用该算法融合各传感器的估计。

因为上述两个难点，现有文献的方法都不再适用，所以下文考虑采用类似文献［15］的最优加权算法进行融合。

2 分布式Kalman滤波融合算法

本文提出的分布式融合算法基于文献［13］和［14］中最优加权融合矩阵的结论。假定x为系统要进行估计的n维状态，是关于x的“局部”无偏估计，且下列的估计误差协方差矩阵已知，即

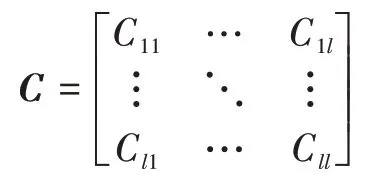
所对应的误差协方差矩阵为

其中，

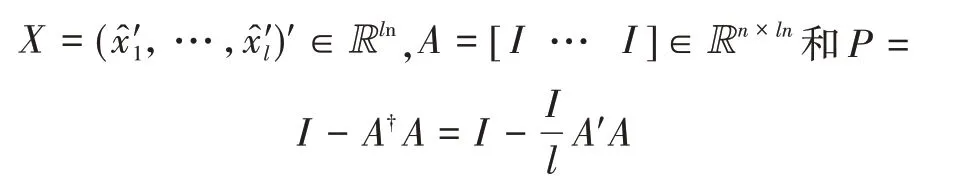
根据上述公式（6）和（7）及文献［11］的融合方法，为形成递推式的融合公式，选择2l+1个“局部”估计，即

根据公式（6），对于具有l个传感器的动态系统（1）和（2），中心式Kalman滤波的最优线性融合估计由下式给出，即

其中2l+1个“局部”估计的估计误差协方差阵为

类似于公式（7），上述融合估计的误差协方差矩阵为

为递推给出的误差协方差矩阵中的元素，首先确定初值如下：

由公式（4）和式（5），可得到如下“局部”估计误差的递推式，即

其中，第二个等号由公式（4）代入得到，第三个等号由合并同类项得到。

类似的，有

其中，第二个等号由公式（5）代入得到，第三个等号由合并同类项得到。

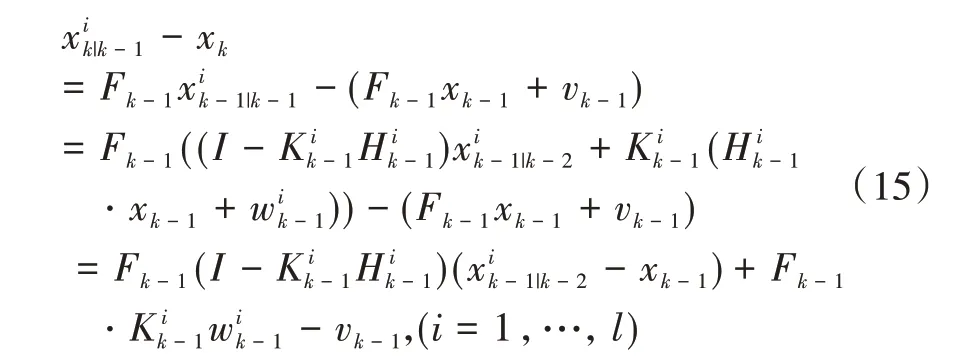
其中，第二个等号由公式（5）代入得到，第三个等号通过合并同类项得到。

更进一步，由公式（13）和（15）可得Ck中各元素的迭代式，即

类似的，由公式（13）和（14）可得

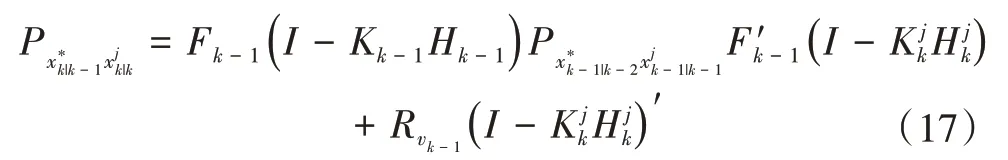
类似的，由公式（14）和（15）可得

类似的，由公式（15）可得

类似的，由公式（15）可得

这样就得到了Ck中的所有元素，从而获得了Ck的递推式，得到最优线性融合估计。

由公式（9）-（20）可以发现，此融合方法不涉及计算矩阵的逆，同时也不要求观测噪声协方差矩阵是对角块的，因此可以很好地解决本文所考虑的分布式估计融合问题。

3 仿真实例

为验证本文所提出的融合算法的性能，下面以实践中广泛应用的两个目标运动模型作为例子进行模拟仿真，例1为目标在三维空间内做圆周运动，例2为目标在二维空间内做直线运动，且目标状态都受到等式约束，从而导致融合过程中估计误差协方差矩阵是奇异矩阵。在本例当中，假设各局部传感器之间的观测噪声是相关的，因此系统的观测噪声方差矩阵是非对角块的。

3.1 例1圆周运动

估计目标在三维空间内做匀速圆周运动，位置向量xk的随机动态系统为

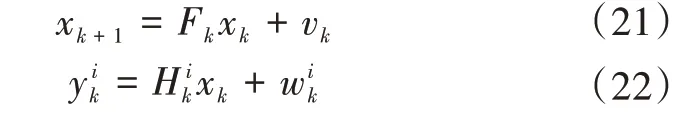
同时假设状态xk受到等式约束，即被约束在矩阵D的零空间中，即

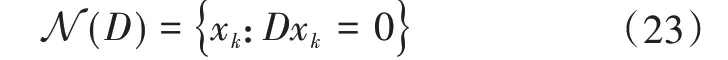
带有约束公式（23）的动态系统公式（21）（22）就转化为无约束系统，即

其中，P=I-D†D，(·)†表示矩阵的广义逆，由于P是奇异阵，所以此时转化后的“转移矩阵”PFk也变为奇异阵。在此例中，假设

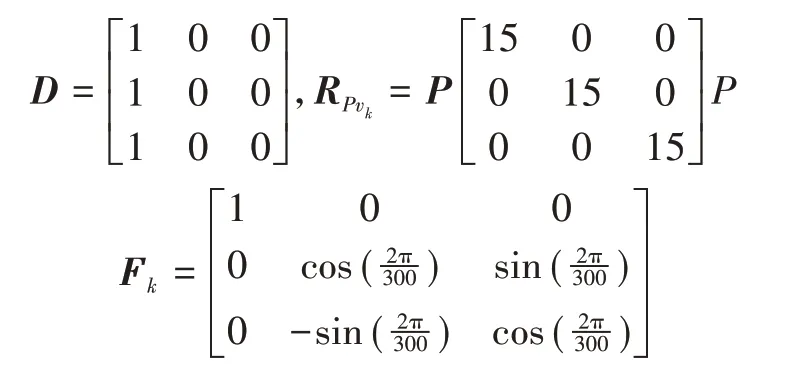
假设系统由两个传感器进行观测，其观测矩阵和带有相关性的观测噪声协方差矩阵以下列形式给出，即

动态系统的初始值设定如下：

利用蒙特卡洛法进行500次模拟，每次模拟Kalman滤波迭代300步，利用平均目标位置向量的均方误差损失Ek评估算法性能，即

其中，表示第i次模拟第k步迭代的融合后的估计值，表示第i次模拟第k步迭代的状态值。

中心式滤波、本文所提出的最优加权分布式融合滤波和文献［2］的融合算法的估计误差数值结果如图1所示。

图1 圆周运动时不同Kalman滤波融合方法的估计误差Fig.1 Estimation errors for different Kalman filter fusion methods of circle moving model

由图1可见，文献［2］算法估计误差曲线在本文所提的最优加权分布式融合算法和中心式融合算法的误差曲线上方，估计误差较大；而本文所提的算法对应误差曲线非常接近中心式融合误差曲线，表明本文所提的算法具有较好的性能。

3.2 例2直线运动

假设目标在二维空间内做匀加速直线运动，状态向量xk∈R4的前两维表示估计目标的位置向量，后两维表示估计目标的速度向量，目标依然服从等式约束，假设观测、转移矩阵如下：

观测噪声方差阵保持不变，等式约束矩阵和过程噪声方差阵设为

初始值设定为

此时，中心式滤波、文献［2］中融合滤波与本文所提的分布式融合滤波的数值结果如图2所示。

由图2可见，文献［2］所提算法的估计误差渐渐发散；而本文所提算法对应误差曲线依然非常接近中心式融合误差曲线，表现出稳健的性能，显示了该算法的优越性。

图2 直线运动时不同Kalman滤波融合方法的估计误差Fig.2 Estimation errors for different Kalman filter fusion methods of straight line moving model

3.3 简要分析

由上述数值结果可以看出，本文所提算法的融合结果误差损失小，远远低于文献［2］中算法的估计误差，具有较高的精确度。仔细分析可以发现，文献［2］所提算法之所以在例1和例2中性能较差，是因为文献［2］中算法要求矩阵R k是对角块的，再由如下等式算出，即［2］

其中，Kk(i)是公式（4）中矩阵K k的第i个列块。利用R k可以分块为，中心式滤波中带观测的项就可以由各传感器的“局部”估计和一步预报线性给出，从而得到与中心式Kalman滤波等价的分布式融合算法。在本文所考虑的系统中，由于不满足对角块的条件，故文献［2］中算法误差较大。

而本文所提出的分布式融合算法性能虽然稍逊于中心式融合，但上述仿真结果表明两者相差不大。此外，在实际应用中，多传感器估计系统可能受到通信量的限制，或者观测出现异常数据，此时分布式融合算法相比中心式算法具有更强的适应性和可靠性。

4 结 语

本文针对噪声相关系统中状态估计受状态等式约束的情况，提出了一个基于线性最小均方误差估计（MMSE）的分布式Kalman滤波融合算法，且融合算法的加权矩阵可以递推得到。最后通过数值实验与中心式滤波进行估计误差对比，验证了该算法具有较高的精确度。另外，实际应用中可能出现观测值异常（比如丢包、延迟等），以及出现观测噪声相关且估计误差协方差奇异的情况。针对该场景，考虑先剔除异常值再融合估计，以得到较好的估计性能，这也是接下来的一个研究方向。