现象教学视角下的“随机事件及其概率”教学设计*

李宏铭 (江苏省苏州市吴江盛泽中学 215228)

传统教学把“知识”当作认识的对象，遵循了解-理解-掌握-应用-评价与创新这一路径.其中的关键词是“理解”，其他的诸个环节都是围绕“促进理解”而进行的，所以有“为理解而教”的口号.而现象教学是把世界当作认识的对象，把知识当作“认识成果”.其基本路径是：现象-问题-探究-反思-知识-……，这个过程没有完结的时候.因为现象分为两种，一种是物质世界中的，一种是理念世界中的.“知识”可以看作理念世界中的“现象”.现象教学的核心观念是“回到问题本身”，口号是“教会学生思考”.它让学生对真实的现象(特例)进行观察，历经感知-设问-抽象-论证，形成认识、诉诸表达，其关键词是“生成”.学生经过了“观察世界—分析世界—表达世界”的过程，积累了活动经验并逐步强化思维能力、提升综合素养，其中的“过程价值”是知识教学所不具备的.

1 教材分析

1.1 教材的前后联系及其地位

“随机事件及其概率”第1课时,首先要让学生确立“偶然性”的观念，破除他们头脑中可能存在的机械的、确定性的世界观,然后再进行量化，即用“概率”来描述可能性的大小.

因为学生在小学、初中已经学习过相关的初步知识，在“偶然性”的观念上学生不是一无所知，因此可以让其直接去感受“随机事件”“必然事件”“不可能事件”，以此唤醒他们的认知和情感.当然这还不够，“可能性的大小”也就是“概率”是必须确立的更高级的观念，只有概率的概念确立了，才是在精确的意义上确立了偶然性的概念.因此高中的这节课是对小学和初中相关课的升华.学生不仅要知道概率是什么，还要知道人们是怎样认识概率的，这才是概率观念的真正建立.

1.2 教学目标

(1)理解随机事件、必然事件、不可能事件的含义;理解概率的定义，知道概率数值的3个来源.

(2)能准确表述相关概念，并直观感知生活中一些随机事件的概率大小;能用概率统计的观点分析随机现象，用概率的知识解释这些现象.

(3)认识偶然性和必然性，提高全面地看待事物的基本素养;知道计算偶然性的大小(即概率)，培养推理和判断的基本能力.

2 教学过程

2.1 直观的概率的生成

(1)感知设问

师：(拿出一枚硬币)这是一枚硬币，你能想到什么？

生：它能买东西，能用它投资赚钱……

师：我们这是数学课，我想请问大家一个问题,抛这枚硬币，它落地后是正面向上吗？

生众：不一定.

师：“不一定”是什么意思？

生众：就是可能发生也可能不发生(随机事件).

设计意图在这里，教师提供帮助，在不知不觉中形成“可能发生也可能不发生”这种表达.这不是对学生回答的刻意扭转，而是用一个“现象”把学生的思考引向了本节课的主题.而且，“可能发生也可能不发生”是学生自己说出来的，这正是“什么是随机事件”的答案.

师：既然可能发生也可能不发生，我们就要考虑什么问题？

生众：概率.(学生初中学过概率)

师：你还能举出哪些随机事件呢？

(学生举例……)

师：是不是说世界上的所有事件都是随机事件？

生：不是的，并非所有的事件都可能发生也可能不发生.

师：用肯定句来表达，怎么说？

生：有些事件是必然发生的，有些事件是必然不发生的.这些都不是随机事件.

师：很好！它们也有各自的名称.必然发生的事件叫必然事件，必然不发生的事件叫不可能事件.下面，请你们分别举出必然事件和不可能事件的例子.

(学生举例……)

师：放学你走出校门，遇到的第一个人是中国人，这是什么事件？

生：随机事件.

师：那么，遇到的第一个人是美国人，是什么事件？

生：也是随机事件.

师：这两个都是随机事件，感觉它们有什么不同吗？

生：可能性的大小不同，也就是概率不同.因为我们是在中国，所以遇到中国人的概率很大，遇到美国人的概率很小.

师：“概率很大”“概率很小”是什么意思？能到多大和多小？

生：能大到1，能小到0.

师：这个1和0是哪来的？

生：是凭感觉.

师：那么我们来感觉一下，抛一枚硬币，正面向上的概率是多少？

生众：二分之一.

(2)抽象论证

师：若说这个概率是其他值倒显得很奇怪，是不是？

生众：是的.

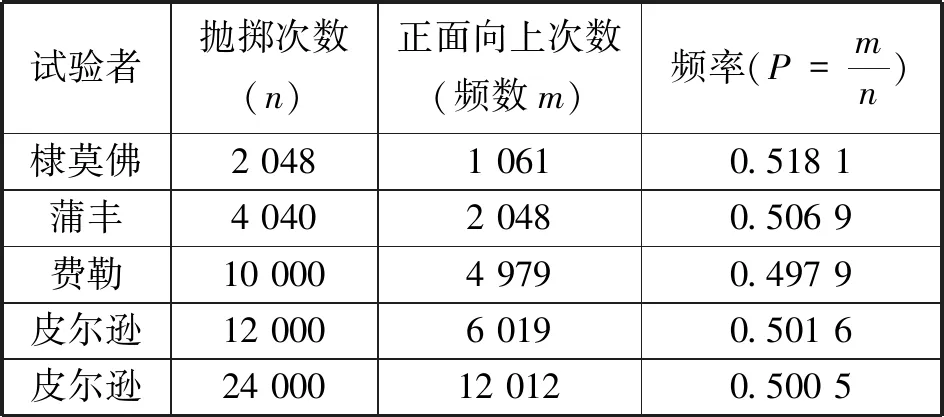
师：但是，人类思想的第一可贵品质就是质疑，经受质疑而屹立不倒的知识才值得信赖.历史上有些学者就对这个“二分之一”产生了怀疑，他们试图做成千上万次试验来验证或推翻它.结果如下表:

试验者抛掷次数(n)正面向上次数(频数m)频率(P=mn)棣莫佛2 0481 0610.518 1蒲丰4 0402 0480.506 9费勒10 0004 9790.497 9皮尔逊12 0006 0190.501 6皮尔逊24 00012 0120.500 5

师：看了这张表，你有什么想法？你认为“二分之一”被验证了吗？被推翻了吗？

生：似乎没有……

师：怎么办？要不要去做更多的掷硬币实验？

生(一致)：不要.

师：那概率究竟是不是“二分之一”？表个态吧！

设计意图让学生表态很重要,从小的方面讲，这牵扯到他对知识的情感态度价值观；从大的方面讲，这牵扯到他人格的独立.有的人一辈子都不知道自己是“可以表态”也“应该表态”的.

生1：我认为就应该是“二分之一”，因为它没有被推翻.

生2：我们一致都认为是“二分之一”，没法接受其他的数值.

师：大家的观点是一致的，这也是全人类的观点(普世价值).现在我们把这个观点明确写下来.

生：掷一枚硬币，正面向上的概率是二分之一.(补充)反面向上的概率也是二分之一.

结论1 掷一枚硬币，①哪个面向上是随机的；②正面、反面向上的概率都是二分之一.

师：我们再来看看另一个常见的东西：骰子.一个正方体，6个面上分别刻有点数1，2，3，4，5，6．那么，掷一枚骰子，6点向上的概率是多少？

生：六分之一.

结论2 掷一个标准的骰子，①哪个面向上是随机的；②每个面向上的概率都是六分之一.

2.2 统计结果的生成

师：你一定听说过：姚明的投篮命中率是48.2%，这里所说的“命中率”是怎么知道的？

生：统计得来的.

师：说具体点？

生：就是用投中的次数除以投篮的总次数，就是命中率.

师：很好！这个“率”是什么率？是“概率”还是“频率”？

(学生活动，可以讨论，也可以自由发言)

师：命中率是统计出来的，因此它实质上是频率.但是，在统计样本比较多的情况下，我们也把频率当作概率来使用，这是数学上的一个规矩.为什么要这样做？就说姚明吧，把他的投篮命中频率当作概率，有必要吗？

生：有，可以衡量他的水平.

师：他的每一场表现观众都能看见，衡量他的水平为什么要把所有场次放在一起计算？

生1：一场比赛不能说明问题，会有波动.

生2：用一场比赛来衡量，可能会拔高他，也可能会看低了他.

师：你是说这不是科学的态度？

生：嗯，不是科学的态度.

师：其实那也不是与人为善的态度，也不是公平的态度.说得真好，请继续.

生：把所有场次放在一起统计，可以作为他的一个稳定值，这个稳定值更有价值.

师：还有什么价值呢？

生：可以评价过去，还可以预测未来.

师：请说具体点.

生：在下面比赛中，我们就可以估计姚明的发挥情况，估计两个队的实力，预判比赛结果.

师：数学上用统计得来的频率当作事件的概率，这是符合我们直觉也符合我们需要的，我们以后就这么做了.不过从数学上看投篮命中率只能统计，硬币正面向上不统计也能知道.这就是概率值的两个基本来源，大致是这样：

结论3 概率值的来源：①直观的概率值(像抛硬币、掷骰子中的概率)；②统计的结果(像投篮、种子发芽)

设计意图直观的概率值其实是先验的知识，统计的概率值实则为经验的知识，这就是人类知识的两大根本来源.

2.3 数学计算结果的生成

师：掷两枚硬币，正面都朝上的概率是多少？

(师生活动)用穷举法：(正，正)，(正，反)，(反，正)，(反，反)，算得四分之一.

师：于是我们知道，概率值还有第三种来源，即③数学计算的结果(像掷两枚硬币).

(和上面的①②写在一起，共同呈现出概率的三大来源)

师：掷一个标准的骰子，偶数点向上的概率是多少？

(学生活动，交流)

2.4 其他现象概率的思考

师：现在，我有这样的一枚骰子(图1)，是自己用土豆做的，为四棱台形，1点被刻在上底面(较小的底面)上，6点在下底面.掷一次这样的骰子，1点向上的概率还是六分之一吗？

图1

生：不是.

师：是大了还是小了？

生：感觉是大了.

师：能知道具体值吗？

生：……看起来就只能实验统计了.

师：我们课后来做这个实验.

(其余零碎概念均让学生看书完成)

3 回顾与反思

3.1 教学设计的立意

这节课的任务是理解概率的概念，那就必然要追问：概率是什么，它从哪里来、要到哪里去(有什么用)？因为这是一节起始课，有多个基本概念需要认识，极易陷入琐碎、零散概念的罗列.这个设计的立意便是淡化对概念的介绍；不搞“一个定义几点注意”，主要精力就放在一件事情上，那就是“概率”意义的生成.为了保证生成的流畅性，充分注意了对直觉的开发与利用.

2.4给出的不规则骰子，提供的还是一个可观可感的现象.用它不是为了产生知识，而是为了产生观念和方法.当然，观念和方法都比知识更重要.知识可以在网上查到，而“需要查什么”“怎么查”以及“查来后怎么用”才是需要解决的问题.

3.2 教学反思

(1)要重视对知识生成过程的教学

人类的知识大致分为两种，一种是直觉的知识，一种是导出的知识.前者基于经验和感性，后者基于逻辑和理性.前者更重要，因为前者是一切知识的基础，也提供了一切逻辑推理的起点.掷硬币、骰子中的概率，是人类的直觉知识，在教学中应当予以承认，并充分利用.概念有四要素：事例(正与反)、特征(本质与非本质)、意义、符号(名词)，这节课里可以说都有了，而且主要是学生自己生成的.

(2)要提高学生自主生成知识的能力

那些零碎的概念，比如“随机现象”等，淡化处理是否可以呢？事实上，哪些事件是必然的，哪些事件是不可能的，也属于人类的直觉，不需要去反复辨析.建构主义观点下的教学，强调知识的发现或再创造，情境教学中的“领悟”，现象教学中的“生成”，皆显示着直觉的客观存在.如果离开了直觉，将造成知识产生得不自然、不顺畅.从现象“顿悟”而来的知识，一定不是逻辑的产物，它必赖直觉而诞生，至于最后呈现为逻辑形态，那是理性加工的结果.

(3)要让学生在现象中领悟到知识

知识具有抽象性，越是高级的知识其抽象程度越高，教学上的困难是天然的.但是，当我们在观念上做了一个小小的转变以后，就有了惊喜的发现：知识是抽象的，它所描述的对象却是具体的.教育应该让学生“认识世界”而不是“认识知识”！如此一来，让学生“面对真实的世界，进行真实的思考”，就很自然了.这节课采用现象教学的观点，呈现的是一个又一个的现象.当然，学生学的不是现象，而是从现象里领会到的知识，再从知识里领会到应用.