一道平面解析几何考题的探究之旅

张 淦 (浙江省新昌中学 312500)

之前笔者参与了浙江省“9+1”高二联考命题工作,命制了一道直线与椭圆的问题,结果学生的解答情况很不好.今年,一次高二校考中使用了这个题目.尽管考试的对象变了,但测试的结果还是不理想.解答正确的学生寥寥无几,绝大多数学生虽然思路正确,但普遍不能将解题过程进行到底.这说明学生对平面解析几何的本质认识不到位，对解析几何中算法的设计、选择、优化能力偏弱.为此,我们针对此题进行了专题教学,通过不同解题策略的探寻、实施、反思和比较，让学生体会平面解析几何的基本内涵——倾向用代数的方法研究几何问题[1]，在问题解决的过程中,根据几何问题和图形的特征,探索解决问题的思路,用恰当的代数方法“解析”几何的问题.

1 问题再现

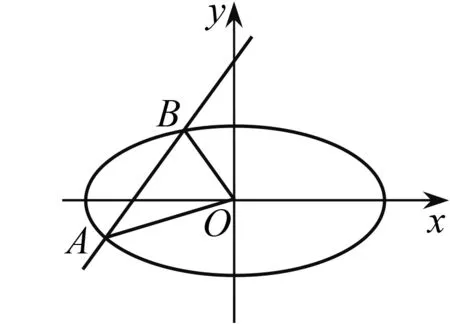
图1

(1)略；

(2)设直线OA,OB的斜率分别为k1,k2,且k1=λk2,求实数λ的取值范围.

2 解法探究

联立直线l和椭圆C的方程,得到k的取值范围.假设A,B两点的坐标,利用两点之间的斜率公式得到k1,k2的表达式,最终建立起λ与k之间的代数关系式.

从解答过程来看,很多学生也是化简到此,无法再继续下去.究其原因,是式中的x1与x2不具有对称性,无法直接使用韦达定理.因此①式的处理是整个问题的关键所在.

策略1 千淘万漉虽辛苦,吹尽狂沙始到金——“直接法”

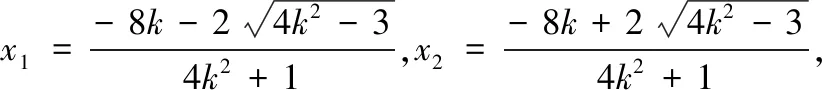
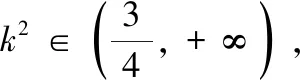
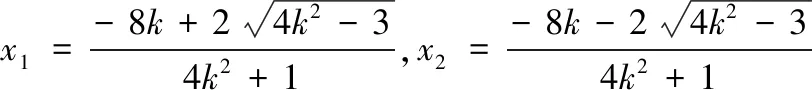
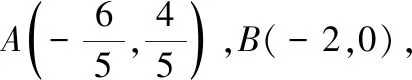
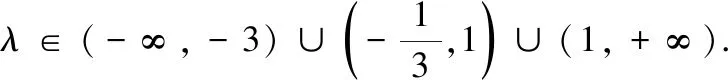
点评 我们在解题时,要理清题目的条件和需要解决的问题,明确问题和条件之间的联系,看透问题的本质，克服“怕运算”的心理障碍,不妨将自然的解题策略付诸实践.

策略2 山重水复疑无路,柳暗花明又一村——“零点代参法”

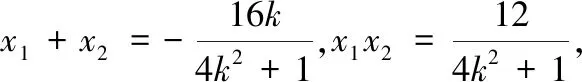
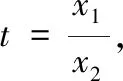
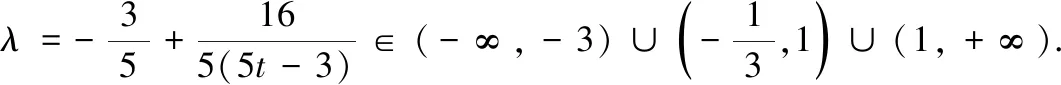
点评 在平面解析几何中,应用韦达定理结构的对称性进行化简计算,学生是比较熟悉的.但是,遇到非对称问题时,很多学生就无从下手.这时需要我们引导学生从“变”的现象中认识“不变”的本质,把握运动变化中的不变性.

策略3 身“有”彩凤双飞翼,心有灵犀一点通——“对偶式法”

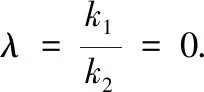
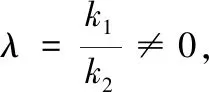
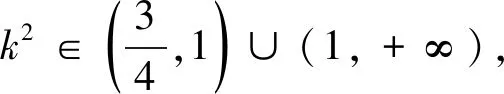
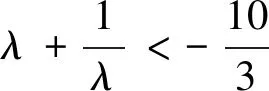
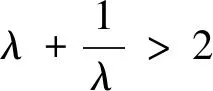
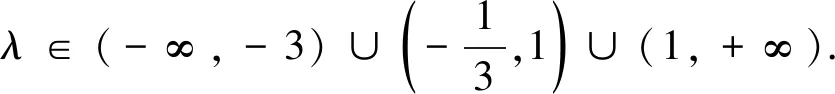
点评 蝴蝶因为有了“双飞翼”,才能翩翩起舞；雄鹰有了“双飞翼”,才能翱翔天地.“双飞翼”是自然界中对称美的生动体现.对偶式是指形式相似并具有一定对称关系的两个数学式子.在数学解题过程中,如果能观察、思考,挖掘条件,构造出潜在的对偶式,往往能使问题迎刃而解.“对偶式法”是数学中对称美的生动体现.

策略4 问渠那得清如许?为有源头活水来——“消元法”

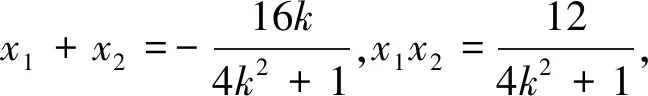
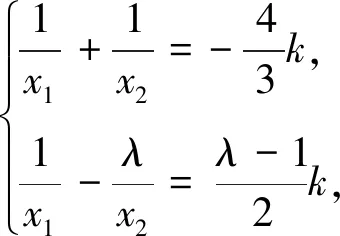
点评 方程思想是一种重要的数学思想方法.用方程思想解题的关键是利用已知条件建立起已知量和未知量之间的数量关系.应当说,平面解析几何中,消元法是最为常见和重要的代数解析方法之一.

策略5 横看成岭侧成峰,远近高低“可相同”——“同构式法”

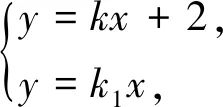
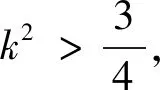
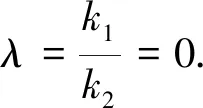
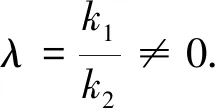
点评 同构式是指结构相同而变量不同的两个或多个表达式.同构式是数学对称美、和谐美的体现,更重要的是合理运用同构式可以培养学生的抽象思维和转化思想,有效提升学生的数学抽象、逻辑推理等核心素养.

3 总结反思

平面解析几何是高中数学中的一大重点和难点,很多学生对解析几何题既有“怕运算”的心理障碍,也存在如何使用合适的代数语言“解析”几何问题的思维障碍.我们认为，在平面解析几何的解题过程中,要特别关注思维的广度：有意识地从不同的数学思想、数学知识方法等层面,设计合理的代数解析方法；在“一题多解”的发散性思维过程中,不断优化知识结构,整合数学知识.同时，要特别关注思维的深度：理解数学中基本的概念、定义、定理等,把握复杂表象之下的数学本质；在“一法通解”的聚焦性思维过程中,让学生有“一竿子打到底”的深层次学习经历.