对偶的混合对称Chernoff型不等式及其稳定性

徐珂，仇恒方，梅静芳

（淮北师范大学 数学科学学院，安徽 淮北 235000）

0 引言

设Rn为n维欧氏空间.如果Rn中的有界闭凸集具有非空内部，则称其为n维凸体.特别地，欧氏平面R2中的凸体称为凸域［1］.设C2={K⊂R2|K为凸域}，Φ:C2→R为实值函数.形如Φ(K)≥0的不等式是常见的一类几何不等式，如经典的等周不等式，Ros不等式等.

设K是面积为A，宽度函数为ω(K,θ)的凸域.Chernoff［2］证明了等 周型不等式，等号成立当且仅当K为圆盘.随后，Ou等［3］定义了凸域K的k阶宽度函数ωk(K,θ)，即

其中H(K,θ)为K的支撑函数.由k阶宽度函数ωk(K,θ)，得到了Chernoff-Ou-Pan不等式

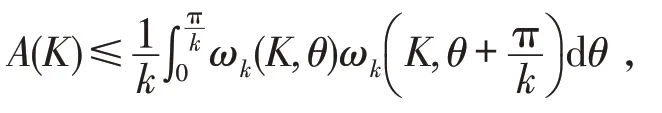
等号成立当且仅当K为圆盘.紧接着，关于两个凸域的混合等周型不等式受到了广大学者的极大关注［4-8］.文献［9］证明了凸域K和L的广义混合宽度不等式

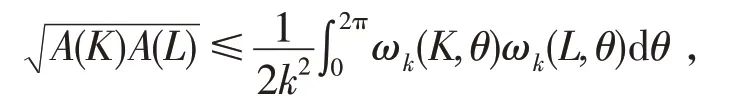
并且等号成立当且仅当K和L均为圆盘.在此基础上，文献［10］进一步推广了两个凸域的Chernoff-Ou-Pan不等式，得到了两个凸域的混合对称Chernoff型不等式

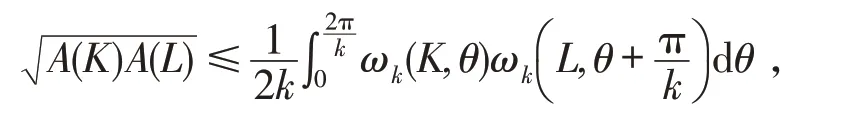
等号成立当且仅当K和L均为圆盘.

受Ou等启发，对于平面星体P（见定义1），Zhang等［11］引入了k阶径向函数ρk(P,θ)：

其中ρ(P,θ)为P的径向函数.借助于k阶径向函数ρk(P,θ)，Zhang等得到了对偶的Chernoff-Ou-Pan不等式

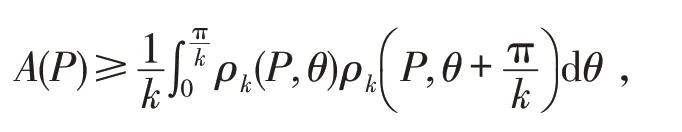
等号成立当且仅当P的径向函数为

同样地，对于两个平面星体P和Q，Mao等［9］也得到了对偶的广义混合径向不等式

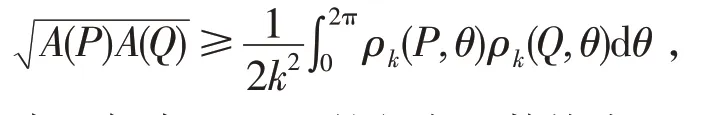
等号成立当且仅当P和Q的径向函数均为

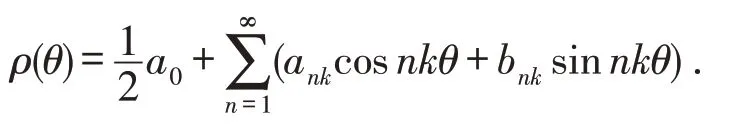
在文献［9］和［10］的基础上，本文首先研究得到平面星体P和Q的对偶的混合对称Chernoff型不等式，即

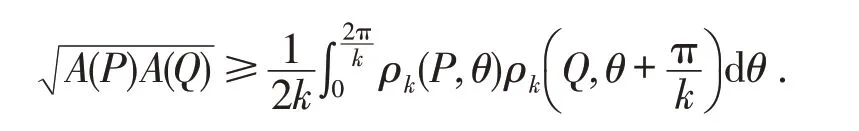
利用星体间的对偶L2度量得到上式的一个稳定性估计.

1 预备知识

本节主要介绍凸几何分析中一些相关概念，更多更详细的相关知识可以参见文献［12-14］.

定义1［12］设P为Rn中的一个紧子集.若P是关于原点的一个星形体，对任意的u∈Sn-1（其中Sn-1为Rn中的n-1维单位球面），则P的径向函数ρ(P,u)定义为

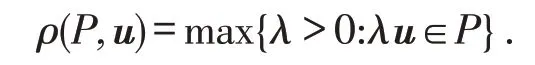
如果ρ(P,u)是连续且为正的，则称P为星体.特别地，当n=2时，P又被称为平面星体.

由于u通常可以由x轴到u的有向角θ决定，不妨记u=(cosθ,sinθ)，用ρ(P,θ)来代替ρ(P,u).显然，ρ(P,θ)是一个连续的且以2π为周期的函数.

设A(P)为平面星体P的面积，由Green公式有

由于ρ(P,θ)总是连续有界的，且以2π为周期，所以ρ(P,θ)可以展开成如下形式的Fourier级数（见文献［9，11］），即

其中

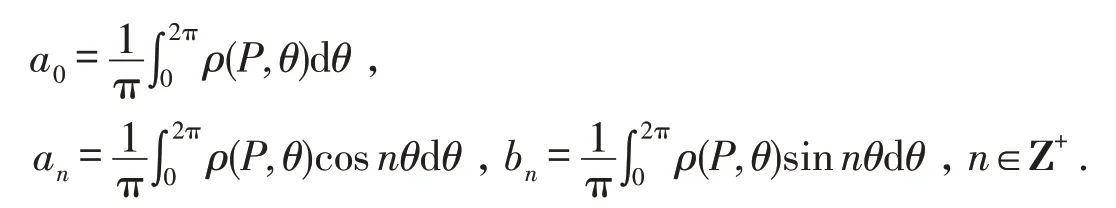
利用式（2）及Parseval恒等式，可以得到

定义2［15］设P为平面星体，如果其径向函数

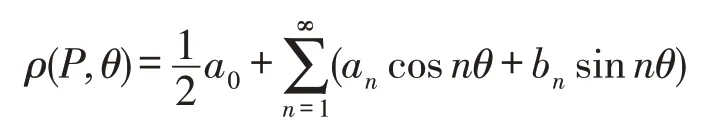
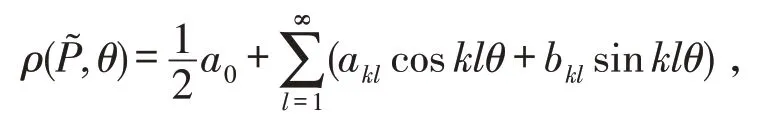
为证明平面星体的对偶的混合对称Chernoff型不等式，需要引入文献［10］中的一个重要的结论.

引理1［10］设f(θ)和g(θ)是以2π为周期的连续有界函数.对于k∈Z+且k≥2，有

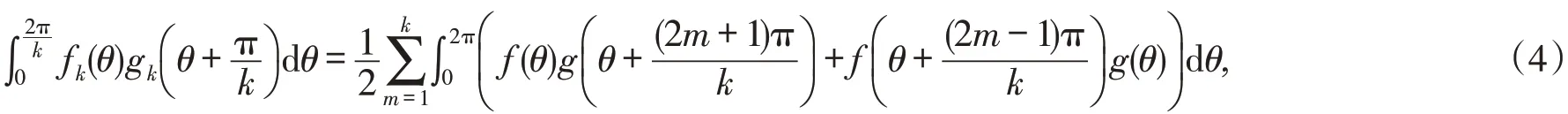
其中

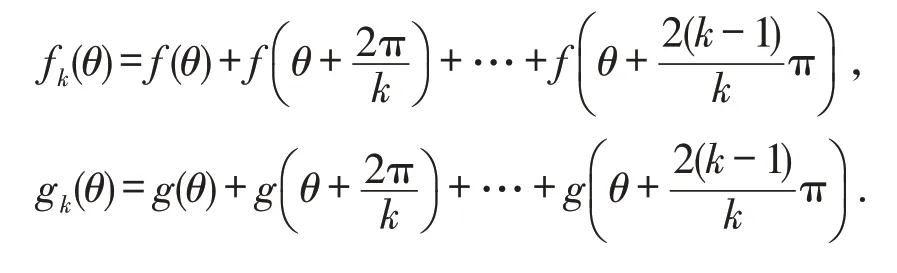
2 主要结果

首先证明两个平面星体的对偶的混合对称Chernoff型不等式，这是本文的重要结果之一.

定理1设P,Q为平面星体.记A(P),A(Q)分别为P,Q的面积.对于k∈Z+且k≥2，有以下不等式成立：

等号成立当且仅当P,Q的径向函数均为

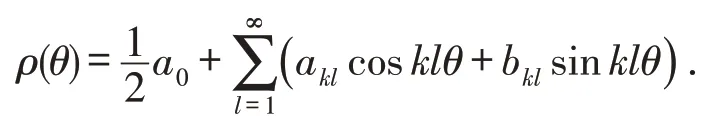
证明由引理1可得

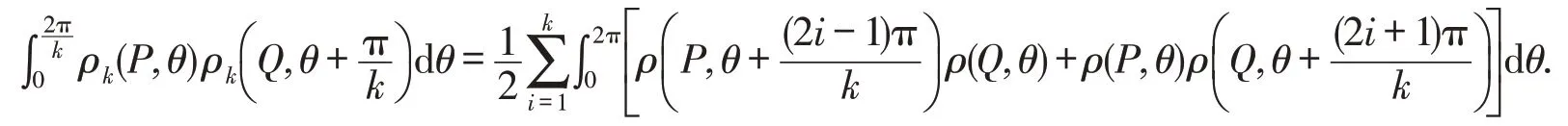
再根据Schwartz不等式和式（1），有

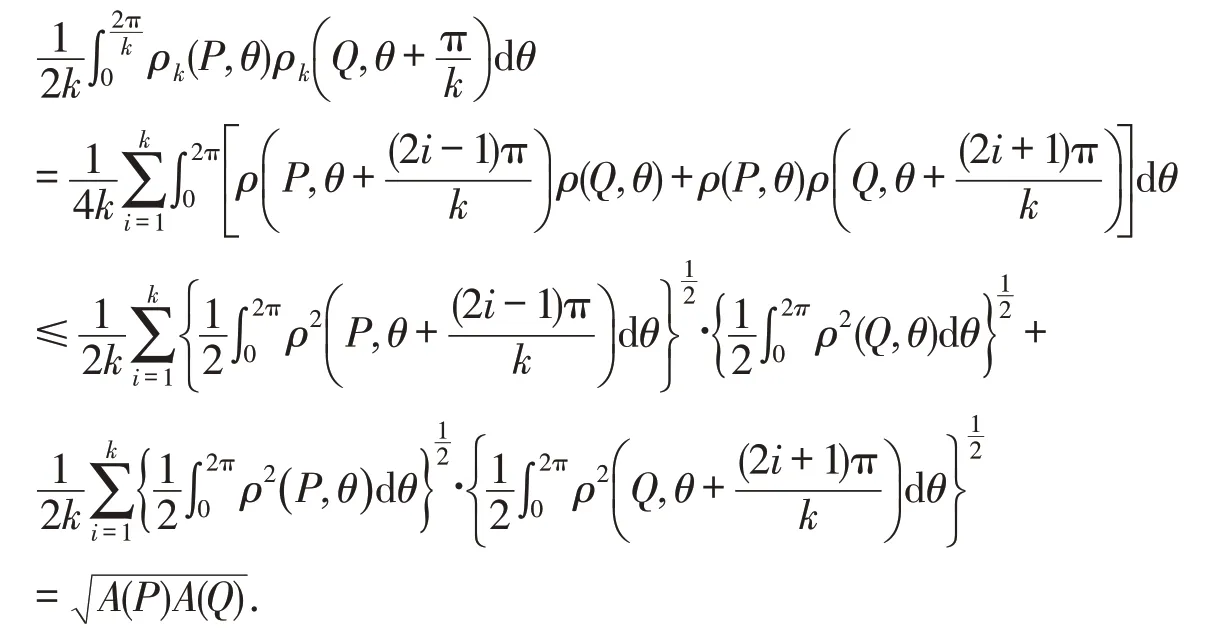
等号成立当且仅当i=1,2,…,k时，

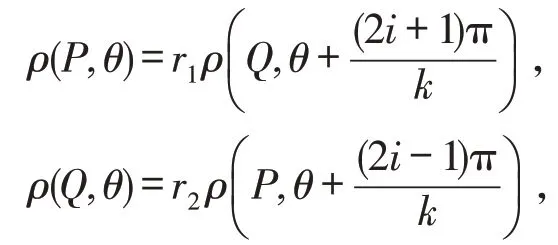
其中r1,r2为常数.从而有

因此r1r2=1，也就是说，P和Q的径向函数满足

结合式（2）可知，i=1,2,…,k时，

当n≠kl,l∈Z+时，an=bn=0.故等号成立当且仅当P,Q的径向函数均为

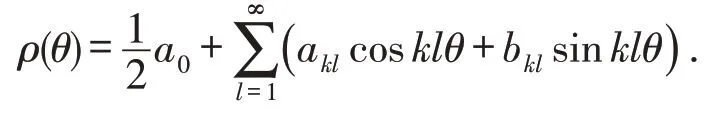
事实上，式（5）左端可以用径向函数的Fourier级数表示出来.

引理2设P,Q为平面星体，则有下式成立：

证明首先由引理1有

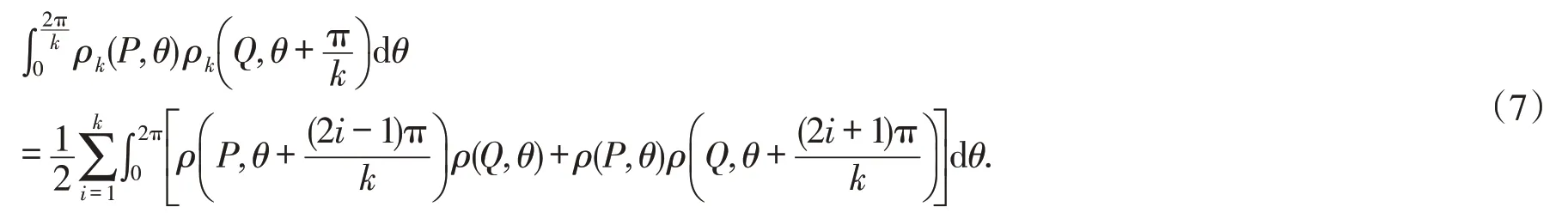
利用式（2），可以得到

同理，

从而，

进而有

再结合式（7）可得

当n≠kl时，.那么

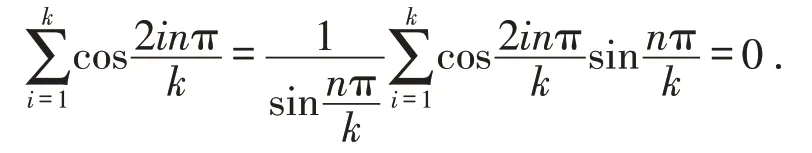
故

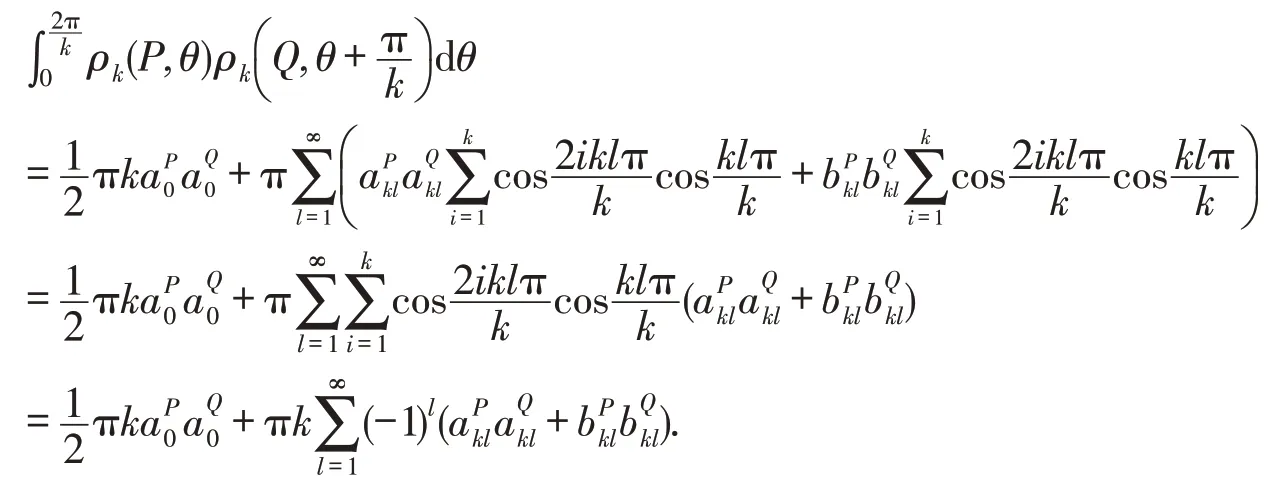
因此，

设P,Q为平面星体.记ρ(P,θ),ρ(Q,θ)分别表示P,Q的径向函数.P和Q之间的对偶L2度量［15］定义为.显然，δ2(P,Q)=0当且仅当P=Q.

下面将利用星体P,Q的k相关星体（见定义2）来刻画平面星体的对偶的混合对称Chernoff型不等式（5）的稳定性.

定理2设P,Q为平面星体.记A(P),A(Q)分别为P,Q的面积，分别是P,Q的k相关星体，则k∈Z+且k≥2时，有

若P,Q为圆盘，则等号成立.

证明首先根据式（3），可以得到P,Q的面积分别为

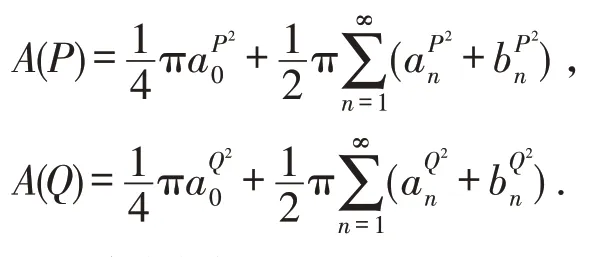
又由引理2的式（6）有

再根据对偶L2度量的定义及Parseval恒等式，可以得到

因此，

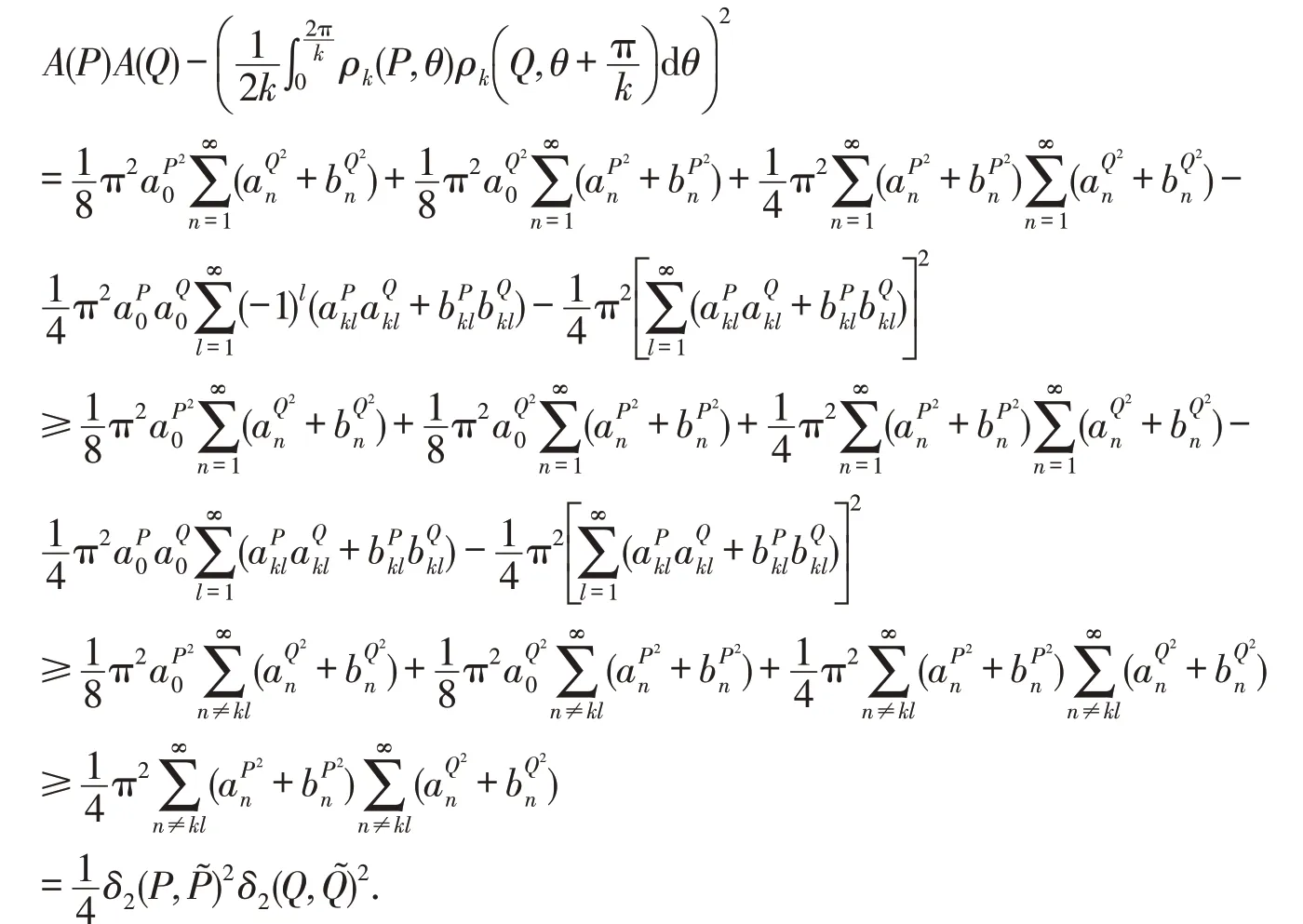
若P,Q为圆盘，显然等号成立.