基于正则化的全双工通信系统非线性自干扰消除方法
管鹏鑫 汪奕汝 赵玉萍
基于正则化的全双工通信系统非线性自干扰消除方法
管鹏鑫 汪奕汝 赵玉萍†
北京大学现代通信研究所, 北京 100871; †通信作者, E-mail: yuping.zhao@pku.edu.cn
针对多径信道和功率放大器非线性特性对同时同频全双工通信系统性能的影响问题, 提出一种基于正则化的联合自干扰消除方案。该方案能够消除线性和非线性自干扰信号, 并且可以缓解传统算法存在的数值不稳定特性。搭建仿真平台对所提方案进行仿真验证, 结果表明, 与传统线性消除和非线性消除方案相比, 该方案具有较高的消除性能增益。
全双工; 功率放大器; 非线性自干扰消除; 正则化
为缓解频谱资源短缺与带宽需求之间日益加大的矛盾, 人们致力于研究能提高频谱效率的全双工技术(co-time co-frequency full duplex, CCFD)[1–2]。与现有的频分双工(frequency-division duplexing, FDD)和时分双工(time-division duplexing, TDD)技术相比, 全双工技术从理论上可以实现双倍的频谱效率, 解决隐藏终端问题, 提高中继通信效率, 增强通信安全性。目前, CCFD 技术已经成为第五代通信技术(5th Generation, 5G)的关键技术之一。
全双工系统工作原理如图 1 所示, 节点 A 和节点 B 在相同时间和相同频率传输信息, 因此本地接收机将接收到发射信号副本(称为自干扰信号 self-interference, SI)以及另一个节点传送的有用信号。强烈的自干扰信号会淹没远端的有用信号, 使得有用信号无法解调。例如, 在无线局域网(wireless fidelity, WiFi)系统中, SI 信号功率比噪声功率高 90dB。
自干扰消除机制可以分为传播域消除[3]、模拟域消除[4]和数字域消除[5]。传播域通过天线或环形器隔离, 自干扰信号到达本地接收机时具有较大幅度的衰减; 模拟域消除是在射频域重建 SI 信号, 并从接收信号中减去, 从而避免接收端模数转化模块(analog-to-digital converter, ADC)饱和, 降低量化噪声; 数字域消除采用数字信号处理技术, 基于估计的自干扰信道和已知发送信号来重建 SI 信号, 并从接收信号中减去。由于技术的局限性, 传播域和模拟域消除并不能将 SI 信号降低到噪声水平, 因此通常需要将 3 种消除机制联合起来, 共同抑制自干扰信号。

图1 全双工系统原理
在实际系统中, 电路中的非线性因素(如相位噪声、功率放大器(power amplifier, PA)非线性效应以及 IQ 不平衡等)均会使系统的消除能力降低。为了传输更远的距离和实现更好的通信效果, 全双工系统的传输功率不断提高, 从而导致 PA 工作在非线性区, 产生高阶干扰。如果仅采用线性自干扰消除, 则无法消除这部分干扰, 从而导致远端传送的有用信号淹没在自干扰信号中, 影响正常通信。PA非线性效应已经成为全双工自干扰消除的瓶颈, 严重地降低系统的自干扰消除性能[6]。有研究仅对PA 的无记忆非线性特性进行建模分析, 提出相应的自干扰消除算法[7–8]。但是, 随着无线通信的传输速率不断增高, 信号带宽也逐步增加。然而, 对宽带信号而言, PA 不仅会产生非线性效应, 并且体现出记忆特性。已有的无记忆特性研究无法精准地符合实际系统, 从而影响系统的消除性能。现有关于存在记忆特性的 PA 非线性自干扰消除的算法采用最小二乘(least square, LS)算法[9], 但求解时存在病态矩阵问题, 导致数值不稳定, 影响消除性能。近年来, 机器学习相关算法与无线通信相结合, 解决了通信领域中的诸多问题。其中, 机器学习中经典的正则化算法可以避免参数过拟合, 并且能够解决数值不稳定问题, 使参数估计更加准确[10–11]。
本文将正则化应用于全双工系统中存在 PA 非线性效应时的自干扰消除。针对线性自干扰消除算法无法消除较强的非线性自干扰信号以及传统非线性消除算法存在数值不稳定等问题, 设计一种基于正则化的联合数字域自干扰消除方案。该方案可以同时消除系统中的线性和非线性自干扰信号, 并将自干扰信号压制到噪声功率水平, 几乎不影响远端有用信号的检测和解调。
1 系统模型
本文研究的场景为两个基于正交频分复用(orthogonal frequency division multiplexing, OFDM)系统传输的全双工节点。由于两个节点硬件结构具有对称性, 因此只选取其中一个节点进行建模及算法研究, 节点的系统框架如图 2 所示。本文讨论的场景中, 节点采用分离天线, 即发射链路和接收链路采用不同的天线。当发射链路和接收链路采用相同的天线, 使用环形器隔离时, 本文所提方案同样适用。
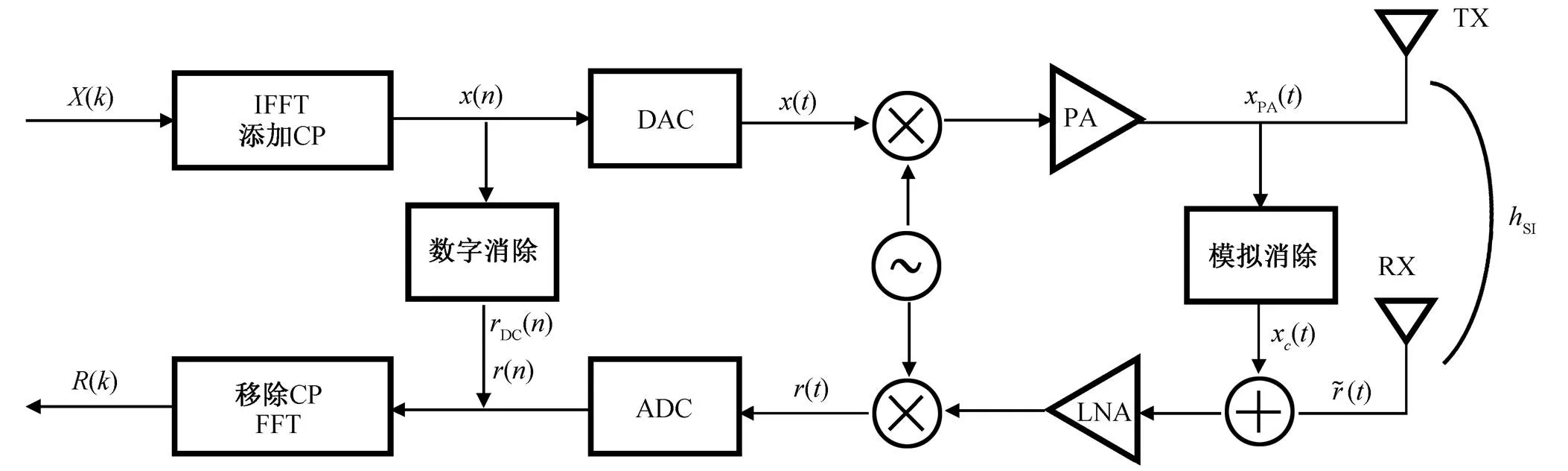
TX和RX分别代表发送天线和接收天线
OFDM 系统共有个子载波,()(=0,1,…‒1)为 OFDM 频域数据, 经过反傅里叶变换(inverse fast fourier transform, IFFT)和添加循环前缀(cyclic prefix, CP)得到时域信号。经过数模转换(digital-to-analog converter, DAC), 模块得到连续信号(), 随后经过上变频和 PA 放大器得到射频输出信号PA()。本文中, PA 模型采用广泛使用的记忆多项式模型[9]。
因此, 可得到射频输出的等效基带数字信号为

其中,()为过采样后的数字信号, 本文过采样倍数为 4, 信号采样速率为 20MHz;=1, 3, 5, …,为非线性的阶数,为最高阶数, 由于只有奇数次高阶信号会对系统产生影响, 因此取值为奇数[9];=0, 1, 2, …,‒1 为对应的记忆深度, 其中最大记忆深度为‒1;a,q代表阶数为, 记忆深度为信号对应的系数。由式(1)可知, PA 不仅产生非线性效应, 并且呈现出记忆特性。
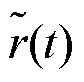

其中, *代表卷积运算,()为高斯白噪声。假设在系数估计阶段无上行信号传输, 因此此处省略远端传输的信号。


模拟消除后的信号经过下变频和 ADC 模块, 成为基带数字信号()。将式(1)代入式(3), 可得()的表达式为
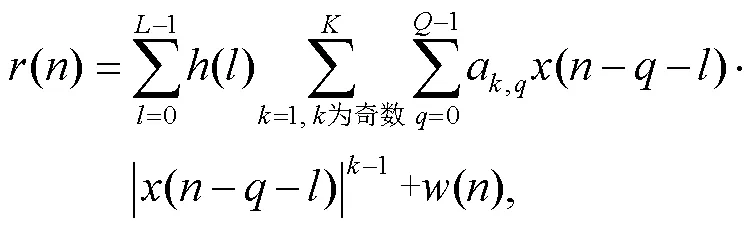
其中, 假设等效信道共有径,()为第径衰减系数。进一步地, 可将式(4)整理为
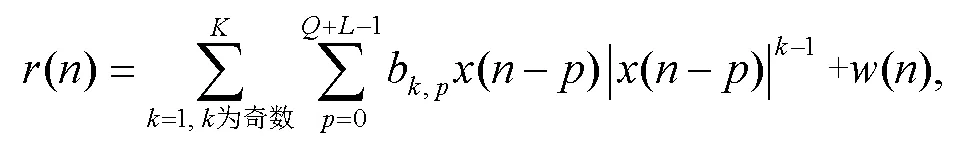
2 正则化联合自干扰消除
2.1 正则化算法
PA 导致系统中存在线性和非线性自干扰信号。为了实现更好的通信性能, 需要对两者进行联合消除。为了便于描述所提方案, 将式(5)改写为矩阵以及向量形式:


由于系数的估计精度直接影响全双工系统的自干扰消除性能, 因此传统方案会降低系统的自干扰消除性能。正则化是一种可以缓解病态特性, 使得矩阵求逆稳定, 提高系数估计精度的方法, 同时可以避免估计参数过拟合。通过引入正则化因子, 将损失函数修正为如下形式:


最后, 将重建的数字域自干扰信号从接收信号中减去, 即可完成自干扰消除:

其中,r为残余自干扰信号。
2.2 正则化因子选择
全双工系统中衡量系统自干扰消除性能的指标为消除能力[8]:

其中,1和r分别为数字域自干扰消除前和消除后的自干扰信号的功率,N为噪声功率。
正则化因子的选择直接决定系数估计的精度, 从而决定系统的自干扰消除性能。如果正则化因子过大, 则相当于对系数进行较大的惩罚约束, 导致系数趋近于 0; 如果正则化因子较小, 则不能实现较好的性能。本文中正则化因子的选取准则是在训练阶段采用蒙特卡洛法, 选取使得自干扰消除能力达到最佳的值, 即

在实际部署时, 可根据系统发射功率, 在训练阶段寻找最优的正则化因子, 随后完成系数的估计, 并将其系数应用于全双工通信系统中自干扰信号的重建和消除。
我们选取一系列值进行仿真, 并分析自干扰消除性能, 如图 3 所示。可以看出, 随着正则化因子的不断增大, 消除性能先增大后减小, 在=10‒5时达到最高。仿真结果表明, 合理地选择正则化因子有助于提高系统的自干扰消除性能。
3 仿真和性能分析
3.1 仿真场景参数设置
为了对提出的消除方案进行验证, 将所提算法与传统的 LS 以及线性自干扰消除性能进行仿真对比, 得出不同发射功率下的系统消除能力等特性。仿真参数如表1所示。

图3 消除能力与正则化因子关系曲线

表1 仿真场景参数设置
图4 发射功率为20和25 dBm时各方案残余自干扰信号功率谱密度对比图
Fig.4 Comparison of power spectral density of residual self-interference signals of different schemes when transmitting power is 20 and 25 dBm
3.2 自干扰消除结果分析
本节对比分析所提算法与传统的线性消除和无正则化非线性消除算法的性能。随着输入信号功率的增大, PA 输出产生的非线性信号变强, 导致带外干扰更强。我们分别选取发射功率 20 和 25dBm 进行仿真, 分别对应高功率和较高功率的场景, 结果如图 4 所示。
由图 4 可以看出, 由于 PA 非线性效应的存在, 系统产生严重的带外干扰, 并且模拟消除无法将自干扰信号完全消除。此外, 仅采用线性自干扰消除无法将自干扰信号降至噪声功率水平, 导致系统仍然存在较强的自干扰信号, 会降低远端有用信号的信噪比。当发射功率较高时, 线性自干扰消除几乎无法消除带外干扰。本文所提方案同时考虑线性和非线性消除, 能够抑制带内和带外自干扰信号功率。本文所提方案可将自干扰信号功率压制到与噪声相当的水平, 具有较好的性能。
3.3 消除能力与发射功率关系
本节主要研究算法消除性能与发射功率之间的关系。发射功率范围为–10~30dBm, 步进为 5dBm, 图 5 显示不同发射功率对应的自干扰消除能力。
由图 5 可知, 随着发射功率增大, 线性消除算法的性能先升高后降低。这是由于系统的非线性自干扰部分随着发射功率的增加而不断增加, 因此, 当发射功率相对较低时, 系统存在的非线性干扰较低, 线性消除即可达到较好的性能, 并且消除能力随着功率的增加而增加。当系统的发射功率继续增加时, 由于仅消除了线性干扰, 较强的非线性干扰留存在残余的自干扰信号中, 由式(11)可知线性消除的性能不断降低。

图5 消除能力和发射功率关系曲线
对比无正则化联合消除与线性消除可知, 当发射功率较低时, 由于传统无正则化 LS 算法存在数值不稳定问题, 影响参数结果, 导致性能略差于线性自干扰消除。当发射功率继续增加时, 即使存在数值不稳定, 但由于算法考虑了非线性干扰消除, 因此消除能仍然会随着发射功率增加, 而不同于图5中红色曲线的下降趋势。
对比所提方案与传统非线性消除可知, 当系统发射功率较低时, 正则化联合消除性能优于传统的无正则化自干扰消除, 其增益约为 5dB, 这是因为正则化较好地缓解了数值不稳定。随着发射功率不断增加, 与传统算法相比, 所提算法的增益逐渐减小。这是因为病态特性表现为待求解变量的估计值, 受观测信号(即本文的接收信号)的影响较大, 而观测信号中包含噪声的扰动。因此, 相比较低的发射功率, 噪声对较高发射功率系统的扰动影响减轻, 从而对数值不稳定的影响减小。
4 结论
本文建立了全双工 OFDM 系统中存在 PA 记忆非线性效应场景下的发射接收信号数学模型, 并对其影响进行分析。我们还设计了一种基于正则化的联合数字域自干扰消除方案。与传统线性消除方案相比, 所提算法能够同时消除线性自干扰以及 PA 产生的非线性自干扰信号, 且消除性能随着发射功率的增加而不断增加。此外, 由于本文算法缓解了系数估计过程中存在的数值不稳定问题, 与传统的非线性自干扰消除算法相比, 具有较高的增益。所提算法可将自干扰功率抑制至噪声功率水平, 具有较好的性能。
[1]Sabharwal A, Schniter P, Guo D, et al.In-band full-duplex wireless: challenges and opportunities.IEEE Journal on Selected Areas in Communications, 2014, 32(9): 1637–1652
[2]Riihonen T, Korpi D, Rantula O, et al.Inband full-duplex radio transceivers: a paradigm shift in tactical communications and electronic warfare?.IEEE Com-munications Magazine, 2017, 55(10): 30–36
[3]Ngo H Q, Suraweera H A, Matthaiou M, et al.Multi-pair full-duplex relaying with massive arrays and linear processing.IEEE Journal on Selected Areas in Communications, 2014, 32(9): 1721–1737
[4]Kim D, Ju H, Park S, et al.Effects of channel estima-tion error on full-duplex two-way networks.IEEE Transactions on Vehicular Technology, 2013, 62(9): 4666–4672
[5]Ahmed E, Eltawil A M, Sabharwal A.Rate gain region and design tradeoffs for full-duplex wireless communications.IEEE Transactions on Wireless Com-munications, 2013, 12(7): 3556–3565
[6]Yilan M, Ayar H, Nawaz H, et al.Monostatic antenna in-band full duplex radio: performance limits and characterization.IEEE Transactions on Vehicular Technology, 2019, 68(5): 4786–4799
[7]Ahmed E, Eltawil A M.All-digital self-interference cancellation technique for full-duplex systems.IEEE Transactions on Wireless Communications, 2015, 14 (7): 3519–3532
[8]Xin Q, Ying L, Dong C, et al.Blind nonlinear self-interference cancellation for wireless full-duplex tran-sceivers.IEEE Access, 2018, 6: 37725–37737
[9]Liu Y, Roblin P, Quan X, et al.A full-duplex transcei-ver with two-stage analog cancellations for multipath self-interference.IEEE Transactions on Microwave Theory & Techniques, 2017, 65(12): 5263–5273
[10]Deschamps G, Cabayan H.Antenna synthesis and so-lution of inverse problems by regularization methods.IEEE Transactions on Antennas and Propagation, 1972, 20(3): 268–274
[11]Pilanci M, Arikan O, Pinar M C.Structured least squ-ares problems and robust estimators.IEEE Transac-tions on Signal Processing, 2010, 58(5): 2453–2465
[12]Zhan S, Hui L, Zhou J, et al.Time domain delay items design for memory orthogonal polynomial predistor-ter // Vehicular Technology Conference.Yokohama, 2012: 12865728
A Regularization Based Nonlinear Self-Interference Suppression Method for Full Duplex Communication Systems
GUAN Pengxin, WANG Yiru, ZHAO Yuping†
Institute of Advanced Communications, Peking University, Beijing 100871; † Corresponding author, E-mail: yuping.zhao@pku.edu.cn
The nonlinear effect of power amplifier causes the strong nonlinear self-interference signal in the co-time co-frequency full duplex communication system, which reduces the communication performance of the system.A joint self-interference suppression method based on regularization is proposed.Taking into account both the multipath channel and the nonlinear characteristics of power amplifier, the proposed scheme can eliminate the linear and nonlinear self-interference signals, and alleviate the numerical instability of the traditional algorithms.To analyze the performance of the method, a simulation platform is built.Numerical simulation results show that the proposed scheme has higher gain than the traditional linear and nonlinear cancellation schemes.
full duplex; power amplifier; nonlinear self-interference elimination; regularization
10.13209/j.0479-8023.2021.094
国家重点研发计划(2020YFB1805102)资助
2020–12–16;
2021–05–24

