全双工多中继网络的中断分析与中继决策

江虹 辜馨月 杨浩

摘   要：为了降低无线通信的中断概率，改善无线网络的通信性能，针对含有多个用户节点与中继节点的全双工无线网络，在考虑聚集干扰与节点自干扰的前提下，分析了网络的中断性能并设计了相应的中继决策方案. 首先，基于Nakagami-m衰落信道条件和放大转发中继策略对网络进行中断概率分析，并求解出相应的闭合表达式. 然后，基于最大带权匹配的思想，根据用户节点对中继节点的渴求度提出一种最小化系统中断概率的最大渴求度匹配算法（Maximum Craving Matching，MCM）来实现中继决策. 最后，通过蒙特-卡罗仿真模拟了不同系统参数条件下系统中断概率变化情况，并验证了MCM算法的有效性. 仿真结果表明，提升节点发射功率能降低系统中断概率，但其改善效果在达到某一特定值后趋于饱和状态，此后继续增加功率对中断性能不再有改善作用. 饱和状态下，与现有部分中继选择算法相比，采用MCM算法的系统中断概率会降低约4%～7%.

关键词：Nakagami-m衰落;全双工;中断概率;中继决策;自干扰

中图分类号：TN929.5                            文献标志码：A

Outage Analysis and Relay Selection in Full Duplex Multi-relay Networks

JIANG Hong，GU Xinyue?，YANG Hao

（School of Information Engineering，Southwest University of Science and Technology，Mianyang  621010，China）

Abstract：In order to reduce the outage probability （OP） of wireless communication and improve the communication performance of the wireless network， this paper investigated a full duplex wireless network with multiple users and relays under the premise of considering  aggregation interference and self-interference （SI）， and designed a corresponding relay selection scheme. Firstly， based on Nakagami-m fading channels and amplify-and-forward protocol， this paper analyzed the outage performance of the full duplex multi-relay network and provided a new closed-form expression of the OP. Then， based on the idea of maximum weighted matching（MWM），according to the user node's desire for a relay， an algorithm named maximum-carving-matching（MCM） was proposed to realize relay selection. Finally， Monte Carlo method was used to display the change of the system OP under the conditions of different system key parameters， and the effectiveness of the relay selection strategy was verified. The simulation results show that increasing the transmitting power can reduce the system OP，but its improvement effect tends to be saturated after reaching a certain value. After that， increasing the transmitting power can no longer improve the OP. In the saturation state， compared with the existing other relay selection algorithms， the system OP using the MCM algorithm can be reduced by about 4%～7%.

Key words：Nakagami-m fading;full duplex;outage probability;relay selection;self-interference

在無线网络通信中，由于环境的多径效应、阴影衰落等影响，部分通信节点间的直连通信链路会变得不可靠，空间距离过远的节点甚至可能无法直接进行通信. 此外，随着无线设备的普及和带宽应用的不断增加，移动数据流向呈现爆炸式增长，有限的频谱资源愈发紧缺，无线网络对提升通信速率、提高频谱利用率的要求日益增强[1-2]. 近年来，为改善无线网络的通信性能，缓解频谱资源紧缺的现状，全双工无线中继网络（Full Duplex Wireless Relaying Networks，FD-WRNs）受到了广泛关注. FD-WRNs能在不提高节点发射功率的情况下扩大网络通信范围，有效提高频谱利用率[3-6]. 然而，在FD-WRNs网络中，接收机的天线不仅会接收到其他发射机的干扰，还会接收到自身天线发送出的干扰，即节点自干扰[7-10]. 同时，在多中继情况下，如果不能合理选择中继节点，有可能会导致网络服务质量下降.

中断概率是衡量无线通信系统的重要指标，为获得更好的通信性能，许多学者在不同的网络环境下对其展开了分析. Koc等[11]和Nauryzbayev等[12]在不考虑直达链路的情况下分别基于Nakagami-m衰落和α-μ衰落对全双工中继系统进行了中断性能分析. Wang等[13]在考虑直达链路和传输延时的情况下给出了放大转发中继策略下全双工系统的中断概率闭合表达式. Zhong 等[14]针对无线携能通信系统（Simultaneous Wireless Information and Power Transfer，SWIPT），分析比较了解码转发与放大转发两种模式下中断概率的性能表现. 但上述文献中涉及的通信系统模型皆为简单的三点两跳网络（即包含一对通信的用户节点与一个中继节点），信号传输过程中不存在节点间互干扰和中继决策的问题，而实际FD-WRNs中通常需要从多个节点中选择合适的中继来完成辅助转发的工作.

中继节点的选择是否合理在极大程度上影响着FD-WRNs的网络通信性能. Gu等[15]提出了一种基于双向拍卖的中继选择策略，以用户节点能获得链路容量提升和中继节点转发时需付出的能量分别作为出价和要价对传统的拍卖模型进行修正，但分析时采用了正交信道，未考虑链路间干扰和距离衰落带来的影响. Chen等[16]对含有两个混合接入点（Hybrid Access Points，HAPs）和多个中继节点的全双工多中继网络进行研究，文中假设只有被选择的中继从休眠模式切换到激活模式，在保证双向通信链路服务质量的前提下进行中继选择;但该模型中同一时刻处在通信状态的节点仅有HAPs和被选择的中继节点，网络中不含其他干扰. Wang等[17]和Atapattu等[18]基于全局信道状态信息（Channel State Information，CSI）给出了一种适用于全双工中继系统的最优中继选择（Optimal Relay Selection，ORS）方案，在考虑直达链路和自干扰的情况下，为了获得更好的通信性能，利用CSI选择使链路信干噪比（Signal to Noise Interference plus Noise Ratio，SINR）最大的节点作为信息传输时的中继节点. 类似地，刘杰群等[19]利用局部CSI在Rayleigh衰落条件下提出了一种最小干扰信号（Minimize Interference Signal，MIS）中继选择算法，MIS算法通过比较部分通信链路的信道衰落系数，从中选出衰落最小的路径以保证信号衰落程度最小，进而降低信号传输的中断概率和误符号率，提升系统的通信性能. 但ORS算法和MIS算法未考虑网络中多用户节点同时通信时链路间的互干扰对网络性能造成的影响.

综上所述，现有文献中，为便于分析，在对FD-WRNs进行研究时大多仅考虑了节点数较少的简单网络或忽略网络中部分干扰，然而实际通信中网络构成往往更为复杂，且网络中的干扰会极大程度上影响通信性能，使用简单网络模型或忽略部分干扰进行分析得到的结果可靠性较低. 因此，本文针对节点自干扰与网络聚集干扰同时存在的FD-WRNs在Nakagami-m衰落条件下分析其通信时的中断性能，并提出了一种适用于全双工多中继环境下的中继决策算法MCM以降低网络的中断概率，提升通信系统的传输性能. 与直接通过SINR或干扰大小进行中继决策的ORS算法与MIS算法不同，MCM算法将根据每个用户对中继节点的需求决定网络的中继策略，最大化发挥网络中每个中继节点的作用.

1   系统模型

本文考虑含有M+N个节点的无线网络，同一时刻下，M个节点作为通信的源节点或目的节点，称为用户节点，N个节点为不能直接通信或直接通信性能不佳的用户节点提供中继服务，称为中继节点. 用 U、R分别代表用户节点集合和中继节点集合，则有U = {ui|i=1，…，M}，R = {rj | j=1，…，N}. 网络中的节点皆为全双工节点，具有激活与休眠两个状态，且仅在通信时处于激活状态，其余时刻都处于休眠状态，激活状态的节点会对其他节点造成干扰. 假设中继节点工作在放大转发模式，所有的通信链路都经历独立且相同分布的Nakagami-m衰落. hp，q（p，q∈U∪R）为节点p与q之间的链路信道增益;Ip，q表示节点p与q通信时，其他处于激活状态的用户节点与中继节点在q处形成的聚集干扰;ISI

p、 βp分别为节点p处的自干扰与自干扰消除系数，其中，ISI

p的值为节点p的发射功率，βp = 1代表未消除自干扰，βp = 0代表自干扰完全消除;dp，q为节点p与q之间的距离;ηp，q为节点p与q通信过程中的加性高斯白噪声（Additive White Gaussian  Noise，AWGN），ηp，q ～ CN（0，σ2）.

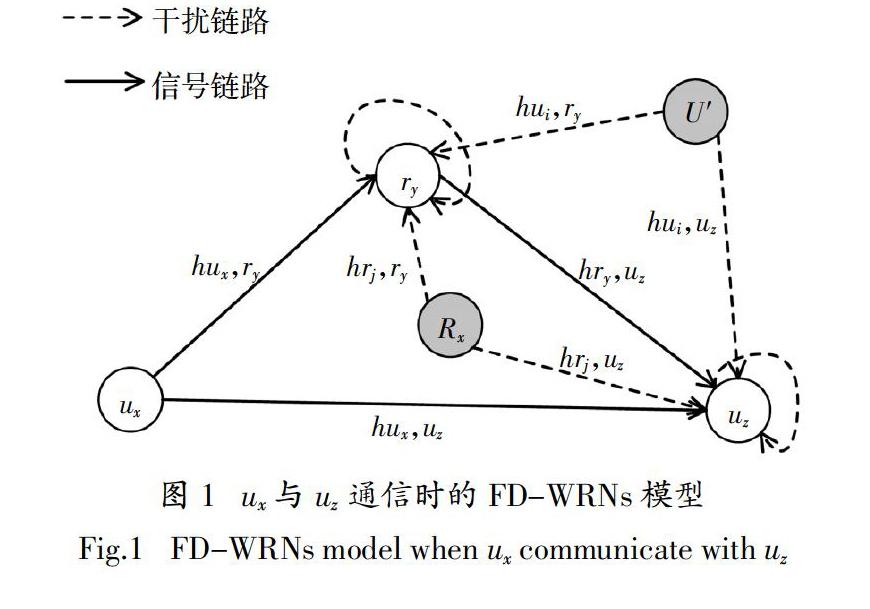
现考虑网络中任意两个用户节点ux与uz进行通信（x≠z，ux、uz∈U），如图 1所示. 图中ry（ry∈R）为 ux、uz采用中继转发方式进行通信时选用的中继节点，R′ = R＼{ry}，U′ = U＼{ux，uz}分别为其他中继节点和用户节点对uz或ry形成的聚集干扰集合.

假设所有的节点都以功率Pt发射信号. 当用户节点ux与uz以直达链路进行通信时，uz处的SINR可表示为：

γ

ux，uz=      （1）

式中：α > 2为路径损耗系数. 此時其他节点在uz处形成的聚集干扰I

ux，uz可表示为：

I

ux，uz= [][i=1，i≠x，z]e

uiPth

ui，uzd-α

ui，uz+

e

rjPth

rj，uzd-α

rj，uz    （2）

式中：e

ui=1、e

rj=1分别代表用户节点ui、中继节点rj发送信号，即节点处于激活状态;反之，e

ui=0、e

rj=0代表用户节点ui、中继节点rj不发送信号，节点处于休眠状态.

同理，在放大转发模式下，当ux与uz通过节点 ry中继辅助进行通信时，中继节点ry与用户节点uz处的SINR分别如式（3）和（4）所示：

γ

ux，ry=      （3）

γ

ry，uz=      （4）

其中，聚集干扰项I

ux，ry和I

ry，uz可分别表示为：

I

ux，ry= e

uiPth

ui，ryd-α

ui，ry +

e

rjPth

rj，ryd-α

rj，ry     （5）

I

ry，uz= e

uiPth

ui，uzd-α

ui，uz +

e

rjPth

rj，uzd-α

rj，uz    （6）

放大转发模式下，协作通信传输的信干噪比可表示为[15]：

γ

ux，ry，uz=      （7）

令A∈{（ux，uz），（ux，ry），（ry，uz）}，链路信道增益 hA的概率密度函数（Probability Density Function，PDF）可表示为[14]：

f

|hA|2（γA） = exp（-μAγA）     （8）

式中：Γ（mA） = vexp（-v）dv为Gamma函数;μA = mA/γA，其中，γA为信干噪比的均值，mA为相应通信链路的Nakagami-m衰落参数，它描述了多径的衰落程度. 由式（1）（3）和（4），γA可表示为：

γA = Pt d-α

A     （9）

式中：B∈{ry，uz}对应着通信时接收信号的节点. A=（ux，ry）时B为ry，A为其他取值时B为uz. 由式（2）（5）和（6），聚集干扰项的均值E（I

ux，uz）、E（I

ux，ry）和E（I

ry，uz）可分别表示为：

E（I

ux，uz）= [][i=1，i≠x，z]e

uiPt d-α

ui，uzE（h

ui，uz）+

e

rjPt d-α

rj，uzE（h

rj，uz）         （10）

E（I

ux，ry）= [][i=1，i≠x]e

uiPt d-α

ui，ryE（h

ui，ry）+

e

rjPt d-α

rj，ryE（h

rj，ry）         （11）

E（I

ry，uz）=e

uiPt d-α

ui，uzE（h

ui，uz）+

e

rjPt d-α

rj，uzE（h

rj，uz）         （12）

2   中断性能分析与中继决策

2.1   中断性能分析

在图 1所示通信场景中，假设成功通信需满足的最低信干噪比阈值为γth，用户节点ux与uz以直达链路通信时的中斷概率可表示为：

Pdir

out=P（γ

ux，uz≤γth）=Fγ

ux，uz（γth）=

exp（-μ

ux，uzγ

ux，uz）dγ

ux，uz=

1-e（μ

ux，uzγth）n =

（13）

式中：F

γu

，u

（·）为γ

ux，uz的分布函数（Cumulative Distribution Function，CDF）;γ（α，x）=exp（-t）tα-1dt，α>0为不完全Gamma函数.

计算ux与uz通过ry中继辅助进行通信时的中断概率. 由于式（7）分母中的常数项1对通信性能影响很小，特别是在高SINR环境下，即γ

ux，ry、γ

ry，uz>>1时，其影响几乎可忽略不计[20-21]. 因此式（7）可表示为：

γ

ux，ry，uz≤  =        （14）

式中：X=γ

ux，ry;Y=γ

ry，uz. γ

ux，ry，uz的分布函数可表示为[11]：

F

γu

，r

，u

（θ）= P

≤θ=P

≤θfX（x）dx=

1-1-FYθ

+ fX（θ+x）dx     （15）

类比式（13），Y的分布函数可表示为：

FY（y）=P（Y≤y）=

exp（-μ

ry，uzγ

ry，uz）dγ

ry，uz=

1-exp（-μ

ry，uzy）（μ

ry，uzy）n =

（16）

結合式（8）（15）（16），有

Fγ

ux，ry，uz（γth）=1-2×exp（-μ

ux，ryγ

th-μ

ry，uzγ

th）×

n

km

ux，ry-1

l（μ

ry，uz）n×

γn+k+l

th       （μ

ry，uzγ2

th）（μ

ux，ry）×

Kk+l-m

ux，ry（2）    （17）

最后，以Pr

out表示用户节点ux与uz以中继转发方式通信时的中断概率，则ux与uz通信时的总中断概率可表示为：

Pout = Pdir

out·Pr

out =

P（γ

ux，uz≤γth）·P（γ

ux，ry，uz≤γth） =

F

γu

，u

（γth）·F

γu

，r

，u

（γth）          （18）

将式（13）（17）代入式（18），可得中断概率的具体表达式.

2.2   中继决策

当无线网络中存在多个中继节点时，某个中继节点可能同时满足多个用户节点的需要，但同一时刻单个中继节点能服务的用户节点数目是有限的. 这种“多选一”的情况下，中继节点为谁提供服务会影响到整个网络的性能. 此部分将以最小化系统中断概率为目的提出MCM算法为用户节点分配中继.

假设每个中继节点同时只能为单个用户节点提供服务，在全双工模式下，用户节点ux与uz可能同时向对方发送信号，此时若只有一个中继为ux与uz之间的通信提供服务，由于该中继同一时刻只能转发一个传输方向的信号，将会导致来自另一个传输方向的信号依然无法被目的端正确接收. 因此，对于全双工模式下无法直接通信或直接通信效果不佳的用户节点ux与uz，应为二者各自分配一个中继节点. 由于最小化网络中断概率与最大化网络成功传输概率等价，所以中继决策问题可转化为：

max[（1-Pdir

out）ω

ux+（1-Pr

out）（1-ω

ux）λry

ux]

s.t.  C1：（λry

ux + λry

uz）≤1

C2：（λry

ux + λry

uz）≤2

C3：λry

ux，λry

uz∈{0，1}，?ux，uz，ry

C4：ω

ux∈{0，1}，?ux         （19）

式中：ω

ux代表用户节点ux与其目的用户节点uz采用的通信方式. 若ω

ux=1，则ux与uz通过直达链路通信;若ω

ux=0则通过中继辅助通信. λry

ux=1表明中继节点ry为用户节点ux提供服务. 约束条件C1表示一个中继节点只能为U中的一个用户节点提供服务. 约束条件C2表示每个用户节点最多只能被分配一个中继，若不等式取值为2则意味着当前通信双方各自选择一个中继辅助通信;为0则表示通信双方直接通信. 约束条件C3表明某个用户节点与某个中继节点之间的状态只有1和0两种，即该中继节点是否为该用户节点提供服务. 约束条件C4表明用户节点之间有直达与中继辅助两种通信方式.

为了减少中继节点的资源浪费，最大程度发挥每个中继节点的作用，本文为每个用户节点设定其对中继节点的渴求度δ，根据渴求度进行网络中继决策. δ具体值取决于该用户节点到目的节点直达链路的中断概率，将用户节点的渴求度与该用户节点通过中继辅助方式通信时的成功概率相乘，其乘积作为此用户参与分配中继时的优先级. 对于任意用户节点ux，直达链路的中断概率越高意味着该节点越需要中继节点的辅助来完成与目的用户节点uz的通信，即相应的渴求度δ

ux越大. 当中继成功概率相同时，渴求度越高的用户节点越有可能被分配到中继节点. 反之，当渴求度相同时，用户节点会被分配到通信成功概率更高的中继节点. 通过上述方法优化 U中每个用户节点的通信方式，即可使整个通信系统的中断概率最小. 用户节点ux对中继节点的渴求度计算方式定义如下：

δ

ux（Pdir

out） = ε（1 - exp（-Pdir

out））      （20）

式中：ε为正实数，确定了渴求度的取值上限. 由于Pdir

out∈[0，1]，指数函数exp（·）在实数域单调递增，因此直达通信的中断概率Pdir

out越高，该式计算所得的渴求度δ

ux越大，即此时该用户节点越需要中继节点进行辅助通信.

借助图论知识，可通过构建二部图将式（19）转化为最大带权匹配问题后用Kuhn-Munkres算法进行求解. 若仅在进行通信的节点之间建边则会出现孤点，因此为保证Kuhn-Munkres算法顺利运行，本文通過构建权值为0，即不具备竞争力的虚拟边将FD-WRNs中的通信场景构建为二部图. MCM算法的细节如下：首先，用U和R中的节点构建二部图中的顶点集. 随后，在U中的每个用户节点与R中的每个中继节点之间补充虚拟边，将边权设置为0建图. 最后，对于直达链路中断概率大于中继链路中断概率的用户节点，将此用户节点与相应的中继节点之间的边权更新为渴求度与中继链路成功概率的乘积. 由此，利用Kuhn-Munkres算法可求解出该二部图的最大带权匹配. 算法1描述了MCM算法的流程.

算法 1：最大渴求度匹配算法MCM

步骤①：根据用户节点集合U与中继节点集合R建立二部图顶点

集V1、V2;

步骤②：对任意ux∈V1及任意ry∈V2，用权值为0的虚拟边连接ux

与ry;

步骤③：若Pdir

out > Pr

out，将ux与ry之间的边权更新为δ

ux（1-Pr

out）;

步骤④：通过Kuhn-Munkres算法求解式（19）;

步骤⑤：返回集合U、R间的最大带权匹配结果，即得网络的中继选

择方案.

3   数值仿真分析

通过蒙特-卡罗仿真和数值仿真在不同的Nakagami-m信道衰落参数 、自干扰消除系数和信干噪比阈值条件下，对比分析无干扰网络情景和有干扰网络情景内中断概率随节点发射功率的变化情况并对MCM算法的有效性进行验证，仿真100次. 取FD-WRNs的用户节点数M = 12，中继节点数N = 10，网络中的节点均匀分布且坐标经归一化处理. 假设所有用户节点都处于激活状态，即eu = 1，?u∈U，中继节点的状态服从伯努利分布. 对于所有的仿真测试，通信过程中的AWGN强度为σ2 = 1，路径损耗系数α = 4，信道链路增益hA2 =1（A∈{（ux，uz），（ux，ry），（ry，uz）}）.

图 2展示了γth = 0 dB，β = 0.05时，不同mA取值条件下中断概率随节点发射功率的变化情况. 由图 2可知，mA取值越大，中断概率越小. 当mA取值相同时，同一发射功率下，无干扰的信道（仅考虑噪声）较有干扰的信道具有更低的中断概率. 当节点的发射功率不断增大时，由于网络中的自干扰和聚集干扰也不断增大，因此，有干扰的信道条件下系统的中断概率逐渐减小后在发射功率达到20 dB左右后开始趋于稳定，而无干扰的信道条件下的中断概率不断降低.

图 3为β = 0.2，mA = 2时，不同γth取值条件下中断概率随节点发射功率的变化情况. 分析图 3可以发现，系统的信干噪比阈值越高，中断概率相对越大. 当节点的发射功率增加到20 dB左右时，系统的中断概率会趋于稳定，此后发射功率的提升并不会改善系统的中断性能.

图 4展示了γth = 0 dB，mA =2时，不同β取值条件下中断概率随节点发射功率的变化情况. 从图 4可以看出，无论β取值如何，中断概率都会随着节点发射功率的增大而减小，最后在发射功率达到15 dB左右时趋于稳定. 当β取值相同时，有聚集干扰场景下的网络中断概率高于无聚集干扰时的中断概率. 此外，如果不消除节点自干扰（β = 1时），即使不断加大节点发射功率，系统仍具有较高的中断概率.

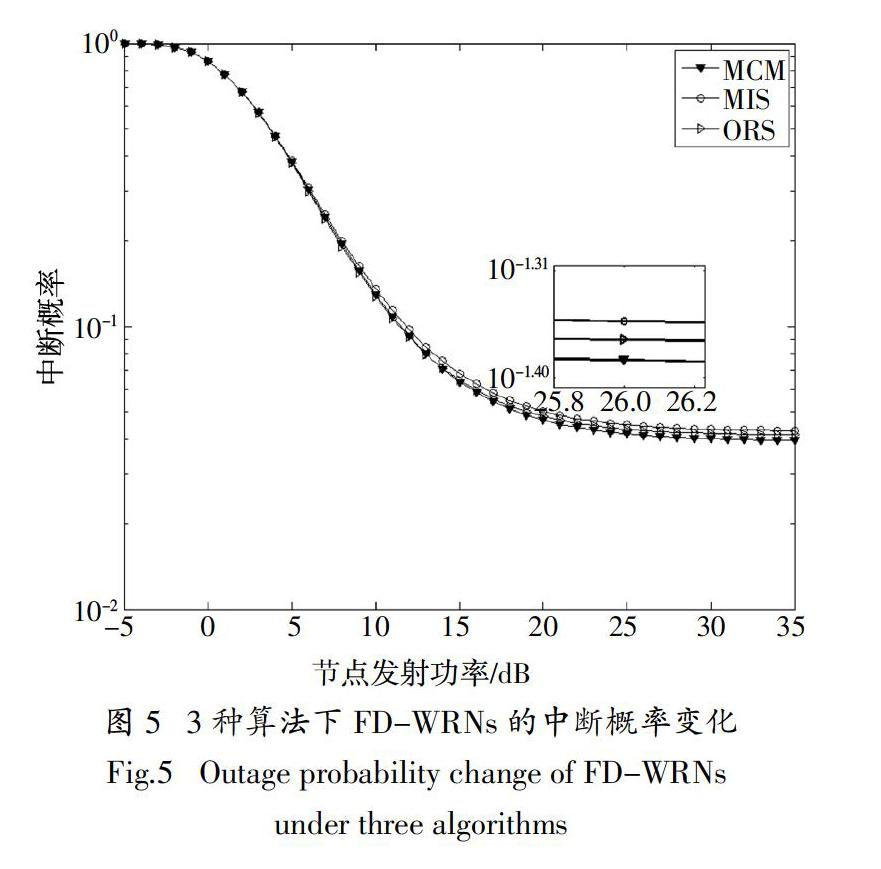
图 5为β = 0.03，mA = 2，γth = 1 dB的条件下，分别采用MCM算法、MIS算法和ORS算法进行中继决策后系统通信的中断概率随节点发射功率提升的变化情况. 从图中可以看出，发射功率提升至约25 dB，即发射功率对中断概率的改善作用达到饱和状态时，MCM算法较MIS算法和ORS算法具有更低的中断概率. 经数值分析发现，此时采用MCM算法得到的系统中断概率比采用ORS算法低约4%，比采用MIS算法低约7%.

由于MCM算法是基于Kuhn-Munkres算法解决最大带权匹配问题，故二者在算法性能上表现类似. 而Kuhn[22] 指出Kuhn-Munkres算法复杂度为O（n3），对于二部图总能求解出其最大带权匹配结果. 因此，Kuhn-Munkres算法保证了MCM算法得到的中继决策方案是全局最优的，但求解过程中需要完备的CSI，且当网络规模较大时，受算法复杂度影响，决策过程耗时较长，节点能耗也会相应增加.

4   结   论

针对自干扰与聚集干扰同时存在的FD-WRNs网络通过蒙特-卡罗法仿真了不同系统参数下中断概率随节点发射功率的变化情况，并对比分析了MCM算法与其他中继选择算法在改善系统中断性能方面的效果，得出以下主要结论：

1）提升节点的发射功率能在一定程度上降低通信的中断概率，但当发射功率达到某一特定值后，加大发射功率对网络中断性能带来的改善作用将会趋于饱和.

2）在FD-WRNs中，自干擾对无线通信的中断性能影响极大，若不进行自干扰消除，即使提升节点发射功率至饱和状态，系统仍具有极大的中断概率.

3）同一仿真环境下，采用MCM算法能够为通信系统带来更低的系统中断概率. 当增加发射功率对系统中断概率的提升效果达到饱和后，采用MCM算法得到的系统中断概率比ORS算法和MIS算法降低了约4%～7%.

4）通过MCM算法虽然能得到当前网络中最优的中继方案，但网络规模较大时，算法复杂度和CSI获取过程为网络节点带来的能耗压力也不容忽视，该问题将在今后的研究中进行优化.

参考文献

[1]    王思源. 全双工双向中继系统的中继策略研究[D]. 北京：北京邮电大学，2019：1—7.

WANG S Y. Research on relay strategies for the full-duplex two-way relay system[D]. Beijng：Beijing University of Posts and Telecommunications，2019：1—7. （In Chinese）

[2]    韩宾，邓冬梅，江虹. 基于功率控制的认知无线网络能效研究[J]. 湖南大学学报（自然科学版），2019，46（4）：115—120.

HAN B，DENG D M，JIANG H. Study on energy-efficient of cognitive wireless networks based on power control[J]. Journal of Hunan University（Natural Sciences），2019，46（4）：115—120. （In Chinese）

[3]   XIE X Z，CHEN J J，FU Y X. Outage performance and QoS optimization in full- duplex system with non- linear energy harvesting model[J]. IEEE Access，2018，6：44281—44290.

[4]    刘逸帆.无线通信系统中的新型中继协作策略研究[D]. 北京：北京邮电大学，2019：7—10.

LIU Y F. Research on new relay cooperation strategy in wireless communication system[D]. Beijing：Beijing University of Posts and Telecommunications，2019：7—10. （In Chinese）

[5]    XIAO Z Y，LI Y，BAI L，et al. Achievable sum rates of half- and full-duplex bidirectional OFDM communication links [J]. IEEE Transactions on Vehicular Technology，2017，66（2）：1351—1364.

[6]   TIAN F，CHEN X，LIU S D，et al. On full duplex scheduling for energy efficiency maximization in multi-hop wireless networks[J]. IEEE Access，2018， 6：2604—2614.

[7]    FIKADU M K， SOFOTASIOS P C， VALKAMA M， et al. Outage probability analysis of full-duplex regenerative relaying over generalized asymmetric fading channels[C]//2015 IEEE Global Communications Conference （GLOBECOM）. San Diego，CA：IEEE， 2015：6—10.

[8]    CHEN X H， LIU G， MA Z， et al. Optimal power allocations for non-orthogonal multiple access over 5G full/half-duplex relaying mobile wireless networks[J]. IEEE Transactions on Wireless Communications， 2019， 18（1）：77—92.

[9]    ARIFIN A S. Success probability in full duplex relay networks using stochastic geometry[C]//2016 IEEE Asia-Pacific Conference on Applied Electromagnetics （APACE）. Langkawi：IEEE， 2016：11—13.

[10]  LI Q，FENG S J， GE X H， et al. On the performance of full-duplex multi-relay channels with DF relays[J]. IEEE Transactions on Vehicular Technology， 2017， 66（10）：9550—9554.

[11]  KOC A， ALTUNBAS I， YONGACOGLU A. Outage probability of two-way full-duplex AF relay systems over Nakagami-m fading channels[C]//2016 IEEE 84th Vehicular Technology Conference （VTC-Fall）. Montreal， QC， Canada：IEEE， 2016：18—21.

[12] NAURYZBAYEV G， ABDALLAH M， RABIE K M. Outage probability of the EH-based full-duplex AF and DF relaying systems in α-μ environment[C]//2018 IEEE 88th Vehicular Technology Conference （VTC-Fall）.  Chicago， IL， USA：IEEE， 2018：20—25.

[13]  WANG Q， DONG Y， XU X D， et al. Outage probability of full-duplex AF relaying with processing delay and residual self-interference[J]. IEEE Communications Letters， 2015， 19（5）：783—786.

[14]  ZHONG S H， HUANG H J， LI R F. Outage probability of power splitting SWIPT two-way relay networks in Nakagami-m fading[J]. EURASIP Journal on Wireless Communications and Networking， 2018， 2018（1）：1—8.

[15]  GU B， WEI Y F， SONG M， et al. Auction-based relay selection and power allocation in green relay-assisted cellular networks[J]. IEEE Transactions on Vehicular Technology， 2019， 68（8）：8000—8011.

[16]  CHEN G J， XIAO P， KELLY J R， et al. Full-duplex wireless-powered relay in two way cooperative networks [J]. IEEE Access， 2017， 5：1548—1558.

[17]  WANG X， YU D Y， LIU Y， et al. Outage analysis for full-duplex cooperative networks with optimal relay selection[C]//2019 IEEE/CIC International Conference on Communications in China（ICCC）. Changchun， China：IEEE， 2019：271—276.

[18]  ATAPATTU S，DHARMAWANSA P，DI RENZO M， et al. Multi-user relay selection for full-duplex radio [J]. IEEE Transactions on Communications， 2019， 67（2）：955—972.

[19]  劉杰群，陈瑾，任国春，等. 能量收集全双工中继网络中的中继选择策略研究[J]. 信号处理，2017，33（1）：116—125.

LIU J Q， CHEN J， REN G C， et al. Research on relay selection strategy of energy harvesting full-duplex relay network[J]. Journal of Signal Processing， 2017， 33（1）：116—125. （In Chinese）

[20]  SONG L Y. Relay selection for two-way relaying with amplify-and-forward protocols[J]. IEEE Transactions on Vehicular Technology， 2011， 60（4）：1954—1959.

[21]  CUI H Y， MA M， SONG L Y， et al. Relay selection for two-way full duplex relay networks with amplify-and-forward protocol[J]. IEEE Transactions on Wireless Communications， 2014， 13（7）：3768—3777.

[22]  KUHN H W. The Hungarian method for the assignment problem[J]. Naval Research Logistics Quarterly， 1955， 2（1/2）：83—97.