基于统计方法对碳排放报告与核查指南中供热碳排放因子缺省值合理性的分析与研究
马亚军
(工业和信息化部电子第五研究所赛宝认证中心(广州赛宝认证中心服务有限公司),广东 广州510610)
1 背景
应对气候变化、全球增温已成为了人们普遍的共识。为应对气候变化,降低温室效应,全球多数国家于1992年签署了《联合国气候变化框架公约》,公约的目标是将全球气温降低到工业革命前的水平。2005年生效的《京都议定书》规定了发达国家需在1990年的基础上减排5.2%,中国属于发展中国家,不承担减排义务。
据统计,中国目前已成为全球最大的温室气体排放国,面对国内的环境压力,国家发改委于2014-12出台了《碳排放权交易管理暂行办法》,并于2013—2015年分别颁布了行业企业温室气体排放核算方法与报告指南[1-2](共24个行业,以下简称“指南”)。其中相关行业指南中规定,企业的外购热力的排放因子缺省值为0.11 tCO2/GJ(即110 tCO2/TJ),用于计算温室气体控排企业外购热力的碳排放量。每年,各省(直辖市)级地方政府委托第三方机构对八大行业的控排企业进行碳排放核查,核查的结果将被用于国家碳排放控排的政策制定。
2 目的
外购热力的排放因子缺省值准确可靠与否,将直接影响企业的碳排放总量的可靠性。理论上,用热企业所需热力除了有自备电厂外,均由热电联产企业提供,则该排放因子缺省值可以认为等于热电联产企业供热排放强度。本文试图通过对热电联产企业碳排放核查报告中供热碳排放强度数据的统计分析(描述性统计及t检验),从统计学的角度对该排放因子110 tCO2/TJ的可靠性进行推断,为相关指南的使用者及主管机构在进行相关决策时提供支撑,以期达到提高碳排放数据可靠的目的。
3 方法
为验证该排放因子缺省值的可靠性,笔者参考了统计学区间估计和假设检验的相关理论。当总体方差σ2未知时,均值μ的区间估计按如下方法确定。由于σ2未知,考虑到σ2的无偏估计量S2,则:

式(1)中:n为样本数量;为样本均值;μ为总体均值;S为样本标准差。
且此分布不依赖于任何未知参数,对于给定的置信度1-α即可计算得t∝/2(n-1),使得:

解以上不等式得:

式(2)中:t∝/2(n-1)为t分布双值临界值。
检验法则为:如|t|>t∝/2(n-1),则否定H0,接受H1;若|t|≤t∝/2(n-1),则接受H0。
根据以上的理论方法,笔者选取了2016—2018年度山东、辽宁、江西、河北省的热电联产企业实际核查的供热碳排放强度,有效数据共103条,数据层级为机组级。核查报告中的数据经过了企业、第三方核查机构、省级政府主管机构委托的复查机构的三级审核,数据质量较高。由于核查任务是由省级政府随机分配的,因此可认为其数据服从正态分布。应用SPSS统计学软件进行统计分析,置信水平1-α选取99%,显著性水平α=1%,供热碳排放强度的描述性统计成果如表1所示。

表1 描述性统计
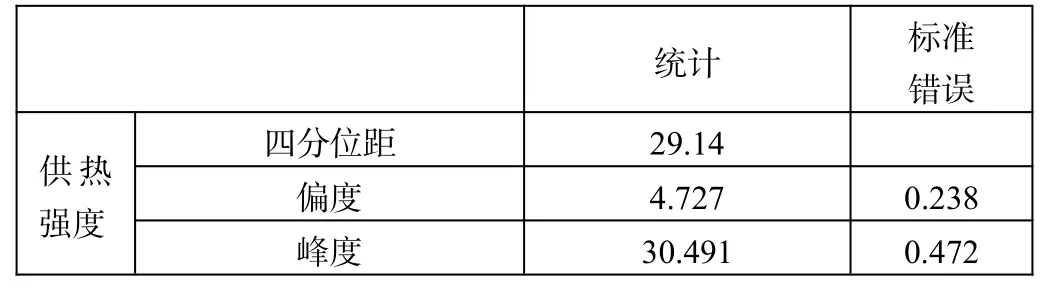
表1 (续)
同时,对排放因子缺省值110 tCO2/TJ执行t检验[3],原假设H0为:μ=μ0,即所有热电联产企业的供热排放强度均值等于110 tCO2/TJ,备择假设H1为:μ≠μ0,即所有热电联产企业的供热排放强度均值不等于110。则样本t值计算公式如下:

式(3)中:n为样本数量;为样本均值;μ0为待检验的值;S为样本标准差。
计算检验p值,自由度为n-1的t分布单尾概率如下:
p=P[t(n-1)≥t],t>0
p=P[t(n-1)≤t],t<0
应用SPSS统计软件分析结果如表2所示。

表2 单样本检验
则检验p值=0.000 055。
4 结论与建议
通过以上分析可以看出,原假设H0成立的概率仅有0.000 055,远远小于显著性水平,说明拒绝原假设H0所要承担的风险足够小(p=0.000 055<α=1%),因此接受备择假设的结论,即所有热电联产企业的供热排放强度均值不等于110的可能性非常高。由描述性统计的结果可知,所有热电联产企业的供热排放强度均值有99%的可能性落在区间(116.182 2,136.667 7)即(126.424 9±8.1019%)之中。
综上,笔者建议主管机构在修订碳排放报告与核查指南时,采用精确度更高的方法和模型对该缺省值进行适当合理的修订,以提高碳排放报告数据的精度,提高可靠性。

