块金效应地质意义及其对品位估值影响

高帮飞 李红兵 张书琛 陈伟康 刘国峰 孙刚

摘要：地质（矿化）连续性评价是矿产勘查和资源储量估算的基础。块金效应为变异函数中块金值与基台值的比值，可以用来刻画地质变量空间结构的变异性，并且对品位估值有重要影响。然而，实际操作过程中，对变异函数的拟合与块金效应的地质解释却显得主观随意。在整合前人研究的基础上，重点探讨影响变异函数块金效应确定的主要因素，系统阐述块金效应对地质（矿化）连续性的指示作用及其对克里格和距离幂次反比等品位估值的影响。本研究对于提升矿产勘查评价和资源储量估算的可靠程度有着现实意义。

关键词：变异函数;块金效应;屏蔽效应;克里格;距离幂次反比

中图分类号：TD11P618.51文献标志码：A开放科学（资源服务）标识码（OSID）：

文章编号：1001-1277（2021）11-0006-08doi：10.11792/hj20211102

引言

块金效应的概念源于金矿研究[1]，最早用来描述相邻样品品位的巨大变化，后来被地质统计学者借用，并赋予较广泛的含义，主要用来表征当观测点间距远大于微观结构的变程时，不能区分出来的那些变化性总和[2]。一般认为，块金效应有2个重要组分：地质或原位块金效应和取样块金效应[3]。近年来，地质统计学者侧重研究取样、制样及化验分析流程对块金效应的影响[3-7]，而关于地质结构对块金效应的影响重视不够。研究表明，块金效应对品位估值有着重要影响[1，4，8-9]，但实际操作过程中，对变异函数的拟合与块金效应的地质解释却又显得主观随意[10-11]。本文在整合前人研究的基础上，以刚果（金）Kalumbwe矿床（下称“K矿床”）为例，重点探讨影响变异函数块金效应确定的主要因素，系统阐述块金效应对地质（矿化）连续性的指示作用，以及其对克里格和距离幂次反比等品位估值的影响，以期对矿产勘查评价和资源储量估算工作有所启示。

1块金效应的定义

1.1块金值

块金值表示变异函数微结构在原点的不连续性[1，12]。块金值——变异函数γ（h）在原点处特征见图1。

1.2块金效应

块金效应在变异函数中定义为块金值与总方差（基台值）的比值[13]。块金效应（ε）计算公式为：

ε=C0/C（1）

基于块金效应的定义，块金效应一般分为以下几类[14]：低块金效应，ε≤25 %;中块金效应，25 %<ε≤50 %;高块金效应，50 %<ε≤75 %;极高块金效应，ε>75 %。

1.3块金效应的组成

块金效应定量描述了非常短距离内样品间的内在变异性。事实上，块金效应的影响范围远不止相邻样本，它实际是叠加在区域变量上的变异随机成分。一般认为，块金效应由采样分析程序及矿床自身内在变异性决定[9，15]。CARRASCO[5]将块金效应分为2类，即反映变程小于样品支集（support）的微结构（自然块金效应），以及取样和（或）分析的测量误差（人为块金效应）。综合认为，块金效应大小主要与以下因素有关：地质（矿化）的不均匀性、样品支集（样品大小，即体积-方差效应）、取样密度（单位空间内的样品数量，即信息效应）、样品取样和化验流程及质量[3-7]。

2块金效应的确定

基于变异函数的块金效应拟合或多或少都受主观因素影响，而这一点常常被忽略。MARCOTTE[11]认为，对于给定的样品数据，块金效应的确定与变异函数模型中结构组分数量和类型选择关系密切。OLIVER等[7]也认为，块金值取值与选取的变异函数模型有关，此外块金值由不受控的小于最小步长（lag）的距离来拟合γ（h），增加了不确定性。然而，大量实践表明，通过开展井向（downhole）变异函数拟合，剔除特异值影响及选取合适样品支集，可以减少主观因素影响，得到可靠的块金值。

2.1井向变异函数拟合

由于块金效应描述的是变程小于观测尺度的所有变异性[1]，因此样品间距最短的方向毫无疑问最能揭示块金效应。实践表明，块金效应的拟合最好采用井向变异函数[16]。一般采用井向变异函数的前2～4点进行模型拟合[17-18]。拟合理论模型可以选择球状模型、指数模型或线性模型，也可以采用线性回归方法[2]。采用球状模型的情况下，模型的切线与纵轴交点即为块金值，与基台值交汇于2/3变程处（见图2）。基台值是井向变异函数趋于稳定的数值，理论上与样品统计方差一致[18]。據此，可以计算块金值与基台值的比值，即块金效应。

2.2特异值影响

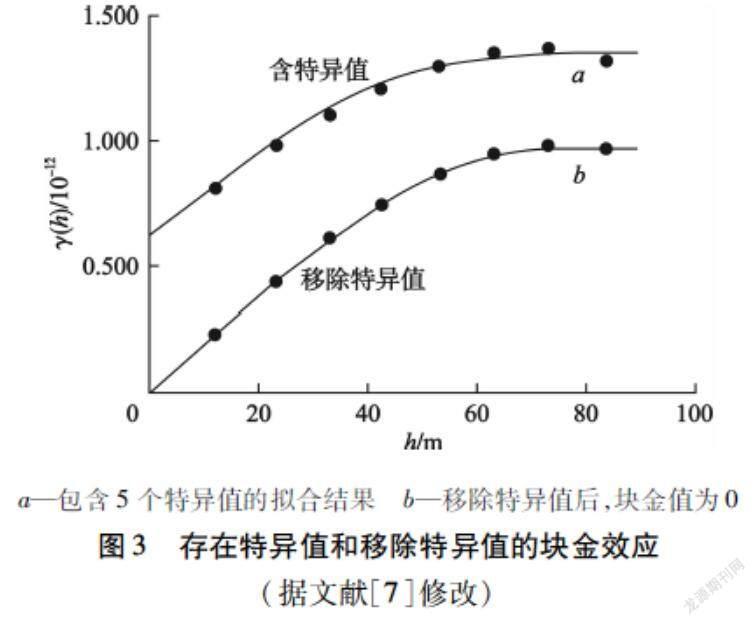
样品数据中存在特异值，且对块金效应产生较大影响。OLIVER等[7]基于400个模拟值得到的实验变异函数及其拟合球状模型显示，存在特异值时，块金值为0.617×10-12，基台值为1.341×10-12;移除特异值后，块金值为0，基台值为1.000×10-12（见图3）。很明显，移除特异值后，块金方差消失。

（据文献[7]修改）为不失一般性，以K矿床为例，进一步考虑移除特异值（特高值和特低值）的情况。K矿床位于刚果（金）铜钴（金）成矿带西段，为典型的沉积层状铜钴矿床[19]。主矿体走向东西，倾向南，倾角60°～80°;长约1 km，厚30～50 m。K矿床由上部氧化矿体和下部硫化矿体组成。勘查阶段主要由钻孔控制，生产阶段采用钻孔+槽探进行联合控制。基本采样间距2 m，圈定工业矿体的指标为铜品位1.00 %、钴品位0.10 %。矿体最小可采厚度和夹石剔除厚度均为2 m。露天采矿台阶高度为10 m。用分形方法剔除特异值，确定矿化域为0.30 %～13.00 %[20]。

通过利用所有勘查数据（以0.01 %为圈矿边界品位，构建隐式模型IM_0.01）、矿化体数据（以0.30 %为圈矿边界品位，构建隐式模型IM_0.30）和工业矿体数据（以1.00 %为圈矿边界品位，构建隐式模型IM_1.00），考察块金效应的变化。采用隐式建模方法以0.01 %、0.30 %和1.00 %为边界品位圈定矿（化）体（见图4），其块金效应拟合结果见表1。由表1可以看出：以0.30 %为边界品位圈定矿（化）体时，块金效应最小;以1.00 %为边界品位圈定矿（化）体时，块金效应最大。比较基台值与样品方差（σ）比值（C/σ2）可以看出：以0.01 %为边界品位圈定矿（化）体时，C/σ2值为0.73，显示有大量低品位、长变程组分，导致结构组分不突出;以0.30 %为边界品位圈定矿（化）体时，C/σ2值增加到0.93，表明低品位背景组分显著减少，总体结构已呈现，矿化连续性好;以1.00 %为边界品位圈定矿（化）体时，C/σ2值大于1.00，可能与矿化结构不完整、缺少较低品位组分有关。

2.3样品支集

研究表明，样品方差和块金效应随着样品支集的增加而降低[21]。利用原始样品数据的方差和不同样品支集組合样品数据的方差，可以计算不同样品支集下的块金效应[16]。假设V0为原始样品支集，组合样品支集为V1，不失一般性有V1=nV0，其中n为组合样品个数。基于空间相关性结构的方差不受组合样品长度影响的合理假设[16]，则有：σ2V1=C0/n+C1，进一步的ε=C0/（C0+nC1），其中C0/n为组合样品支集V1的块金方差，ε为组合样品数据的块金效应。显然，组合样品个数越多，即样品支集越大，块金效应越低;原始样品组合后，样品方差和块金效应均迅速降低（见图5）。为真实反映样品数据的块金效应，实践中，一般对原始样品长度进行统计，按照具有统计优势的样品长度进行等长组合[22]。

3块金效应的地质意义

块金效应与微结构和取样化验偏差有关。理论上讲，系统误差（如测量中的一致偏差）不会成为块金效应的一部分，因为当一个样品值从另一个样品值中减去时（xi-（xi+h）），其就会消失[15]。当然，机械岩心钻探、反循环钻探、炮孔的样品支集，以及取样精度等不同，同样会导致块金效应的变化。美国新墨西哥州Ortiz金矿床不同类型样品的井向变异函数（见图6-a））显示，炮孔样品具有更大的波动及高块金效应[23]。K矿床1 290～1 370 m标高钻孔和探槽数据拟合结果揭示，探槽样品的均值、方差比钻孔数据略高。探槽井向变异函数（见图6-b））显示，其变异性较钻孔数据要复杂，有着相应较高的块金值和块金效应。这些特征显示出探槽数据尽管也能表征矿体品位特征，但由于勘查方法不同，其表现出来的样品数据连续性相对较差。

块金效应与区域化变量的属性特征有关[10]。前人大量研究表明，块金效应所揭示的微结构与宏观地质结构有密切的联系。一定程度上，块金效应可以作为地质（矿化）连续性的测度。

DOMINY等[24]研究了块金效应与矿化结构的关系。在40 m钻孔间距条件下，贱金属矿床矿体总体连续性较好，所有钻孔均见到了工业品位（见图7-a））。全向变异函数显示块金效应为25 %，地质统计学变程为60 m，比40 m的钻孔间距要大，指示了40 m钻孔间距能较好代表地质和品位的连续性。含金石英脉的地质连续性可达几百米，但高金品位被限制于地质连续性仅有几米的局部透镜状含金石英脉中（见图7-b））。全向变异函数显示为纯块金效应特征，40 m的钻孔间距无法解决局部地质和品位连续性问题。21个钻孔中只有2个达到工业矿体品位，要解决此类矿体的连续性问题，需要将钻孔间距加密到5 m。

同样，在巴布亚新几内亚独立国的Ridges金矿项目中，样品的取样、制备和分析的质量控制流程都非常标准，采样及分析误差对块金效应的贡献忽略不计。对纯块金效应的地质解释是，金-菱锰矿脉经强挤压应力作用，矿体破碎成小碎块分布于整个矿化空间（见图8），失去了原始的空间相关性[5]。

4块金效应对品位估值的影响

4.1屏蔽效应

克里格估值算法是一个局部估值工具，其显著特征是具有屏蔽效应[25]。屏蔽效应是指距离待估矿块较近样品点对距离较远样品点的屏蔽效应，即在对待估矿块的平均品位进行估值时，距离较近样品点的贡献更大。更具体来说，只有待估矿块附近的样品点或矿块才能被赋予较大的权重，尤其是当块金方差与总方差比值较低时更为明显[7]。或者说克里格估值算法可看作一种低通滤波器，块金值越大，过滤越强[26]。当块金效应很小或者不存在时，已知样品点的克里格权重系数大小受屏蔽效应影响，当块金效应增大，屏蔽效应相应减弱;当为纯块金效应时，所有样品点相互独立，权重系数相等，屏蔽效应消失[27]。

如果变异函数的结构较好，也就是具有相对较低的块金效应，估值时只采用待估矿块周围第一圈的少量数据。这是因为待估点附近的样品点数据会把距离更远的样品点数据屏蔽[28]。考虑到图9-a）中的数据构型，假设构造上各向同性，也就是各方向上变异性相同。n=8的数据点（编号为Z1～Z8）有着相同的自然属性和相同的样品支集，克里格估值算法给出以下权重[1]：①由对称关系得出，λ2=λ3，λ6=λ5;②由不等关系得出，λ1≥λi，2≤i≤8;③λ7≤λ4，因为Z4屏蔽了Z7的影响;④λ8≥λ4，Z4的部分影响分散到Z5、Z6和Z7。

负克里格权重与低或者零块金值有关[26]。由图9-b）可知，离待估值点较远的外围样品点被赋予小的负权重，其被参与矿块估值样品点（+）所屏蔽[29]。这种情况下，负权重通常非常小，只有其他样品点权重的1/100或者更少。通常，出现负克里格权重表明[17]：①样品点位置被其他与待估值矿块相关的数据点屏蔽;②变异函数模型有着较高程度的连续性。这种特殊的权重模式在连续性最大时最强烈（如零块金效应和长变程），随着块金效应增加，这种模式变得不那么显著[17]。

纯块金效应对克里格权重的影响微乎其微[28]。对于纯块金效应，所有数据都有相同的样品支集，因此有着相同的权重，而不考虑与待估值矿块的距离。较近样品点不再屏蔽更远距离样品点的影响，因此可以说，纯块金效应消除了屏蔽效应[1]。

4.2平滑作用

克里格的平滑作用会导致估计方差降低，引起高值低估、低值高估现象[7]。平滑程度取决于块金效应和变程的相对大小[30]。块金效应越大，平滑作用越强，也就是说，样品的权重更均匀（见图10）。如果块金效应足够低，则矿块的平均品位可以从最近的样品点品位得出;否则，矿块品位则是变程影响范围内样品的加权平均[9]。直至块金效应为1时，平滑作用才消失[7]。在纯块金效应的情况下，估值构成了一个简单的移动平均值[30]。

4.3估值精度

块金方差影响估值精度[7]。克里格方差包含了理论变异函数中的块金方差，换言之，克里格方差不可能小于块金方差。因此，块金效应的确定影响克里格权重，反过来又影响克里格估值方差[18]。如果低块金方差被0代替，那么克里格估值方差会明显降低[31]。同时，由于高品位域的连续性增强，估值的品位风险也会增大。降低块金方差、提高估值精度的常见做法是提高取样、制样和化验工作的质量，减少人为影响[3，32]。

5讨论

5.1观测尺度

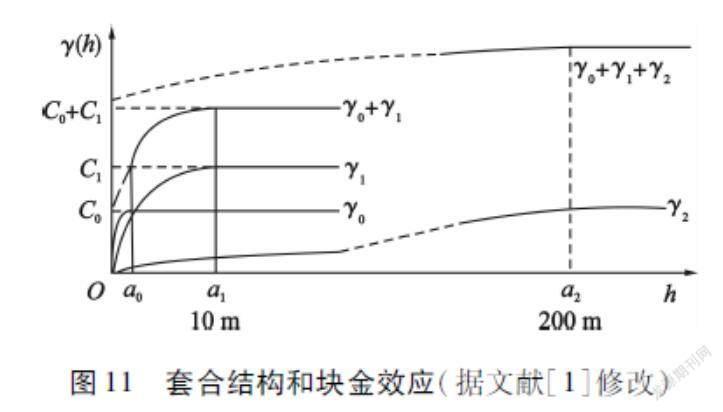
块金效应与观测尺度有密切联系[1-2，33]，但无法同时观测到所有尺度的變异性。例如：采用3～5 m取样网格数据，可以区分变程10 m的结构。但是，如果采用30～50 m取样网格数据，则无法区分这个结构，而只能把小于30 m的变化性放到块金方差中表现出来。这种块金效应的含义依赖于观测尺度的现象被称作块金效应的尺度效应。小观测尺度的结构组分，在大观测尺度上可能表现为块金效应;同时，大观测尺度上应包含块金组分，但可能无法识别，除非样品数据落入块金方差的变程范围[1]。因此，要想了解微观变化性的结构特征，只靠大观测尺度的数据信息是不行的，必须掌握不同观测尺度的样品信息（所谓的信息效应），也就是需要加密取样点[1-2]。这样有了2个不同观测尺度的数据，才有可能研究套合结构（Nested structures）及可能的块金效应。但是，如果品位完全是典型的随机变量，则不论观测尺度大小，所得到的实验变异函数曲线均接近于纯块金效应模型[2]。

变异函数的套合结构可以很好解释观测尺度对块金效应的影响（见图11）。变异函数分析可以定义3个主要的方差区域[1，34]：小观测尺度方差γ0（h）（块金效应），以短变程为特征（a0=2～4倍样长），包含了所有的显微变异性，如测量误差、岩性变化等;中观测尺度方差γ1（h）（几何各向异性），有相对较大的变程（如a1=10 m），以透镜状为特征;大观测尺度方差γ2（h）（带状各向异性），可能是第3个组分变程（如a2=200 m），代表了蚀变地层或者均匀矿化带的延伸。在较短观测距离（h<30 m）时，观测的总变异性取决于γ0（h）+γ1（h），大观测距离总变异性取决于所有的γi（h）。

5.2矿化域的圈定

资源量估算矿（化）体圈定的一个基本原则是保持矿化域内地质和统计特征的一致性[35]。从表1可以看出，以0.30 %为边界品位圈定矿（化）体时，块金效应仅为1.30 %，最大程度突出了变异函数结构组分，既避免了与估值无关的长变程、低品位组分的干扰，也减少了对中变程结构组分的人为破坏。

然而，具体采用矿化域内数据还是域外数据参与估值则取决于矿（化）体的边界分析[35-36]。本文基于图4的隐式模型，对比了以0.30 %和1.00 %为边界品位圈定矿（化）体进行边界条件分析，结果见图12。由图12可以看出：当边界品位为0.30 %时，域内外品位呈明显的渐变过渡关系，为典型的软边界条件;当边界品位为1.00 %时，域内外品位呈硬边界条件。不同矿（化）体及样品数据条件下的克里格估值结果见图13。由图13可知，与生产数据相比，当边界品位为0.30 %时，采用域外数据进行估值的结果（IM_0.30-0.01）与实际值最为接近。从K矿床氧化矿体的总体估计来看，在低块金效应背景下，最大程度保持矿化结构组分的圈矿条件（边界品位为0.30 %）为最佳实践。

5.3估值参数

传统距离幂次反比（IDW）法中样品权重的确定并不受屏蔽作用影响[25]，而是和待估值矿块与已知样品点的距离和幂次选择有关。但是，对于IDW方法而言，随着幂次的增大，离待估值点越近样品点的权重就会越大，类似于屏蔽效应[36]。因此，可以据此建立IDW估值参数与块金效应的联系[1，36-37]。

1）距离幂次的确定。块金效应是选择幂次非常有用的工具。低块金效应指示了空间样品很好的可重复性。这意味着靠近待估值点的样品品位与待估值点很接近，可以采用较高的幂次。相反，高块金效应表明重复性差，应该采用较小的幂次[37]。纯块金效应情形下，估计值为简单移动平均值[30]，幂次可以为0。此外，对于给定的块金效应，较大的变程减少了待估值点附近样品点的克里格权重系数。因此，对于低块金效应和短变程条件下的类似屏蔽作用，只有紧邻待估值矿块的样品点才在品位估值中起到作用[8]。

2）搜索半径的确定。如果数据密度足够，且变异函数有界，较小块金效应情况下，屏蔽作用较大，搜索半径可以接近变程，因为超过变程的样品点数据权重微乎其微。块金效应较大时，屏蔽作用减弱，搜索半径要大于变程，因为远距离样品也可能有权重，尤其是样品数据稀疏时，超过变程样品点的权重可能比较大[7]。

李红兵等[36]提出了基于变异函数块金效应和变程分析的IDW估值工作流程，并成功应用于中亚某金矿床的品位估值。COOMBES[37]系统总结了IDW幂次（屏蔽作用）与块金效应（变程大小）之间的关系（见图14）。然而，具体估值应用过程中，幂次的选取需要结合块金效应反复试验，直至与实际品位分布相近。

6结论

1）块金效应可以刻画地质变量空间结构的变异性。这种变异性的呈现与测量尺度有关。一般情况下，块金效应越低，结构性越好，相应测量尺度下的地质（矿化）连续性越强。

2）块金值拟合具有较强的人为因素。推荐最佳实践为：基于剔除特异值（特高值和特低值）的矿化域品位数据，采用接近实际取样样长的等长组合样品，选取井向变异函数中前2～4点进行拟合。

3）块金效应对品位估值有重要影响。对克里格法而言，块金效应越大，屏蔽效应越弱，平滑作用越强，估值方差（精度）越低。采用IDW估值时，进行变异函数的块金效应拟合可以帮助确定幂次。块金效应较小时，应选择较高的估值幂次。

[参 考 文 献]

[1]JOURNEL A G，HUIBREGTS C J.Mining geostatistics[M].London：Academic Press，1989.

[2]王仁铎，胡光道.线性地质统计学[M].北京：地质出版社，1987.

[3]PITARD F F.Exploration of the "Nugget Effect"[M]∥DIMITRAKOPOULOS R.Geostatistics for the next century.Springer：Dordrecht，1994：124-136.

[4]HOFMANN T，DARSOW A，SCHAFMEISTER M.Importance of the nugget effect in variography on modeling zinc leaching from a contaminated site using simulated annealing[J].Journal of Hydrology，2010，389（1/2）：78-89.

[5]CARRASCO P C.Nugget effect，artificial or natural？[J].The Journal of the Southern African Institute of Mining and Metallurgy，2010，110（6）：209-305.

[6]DOMINY S C，EDGAR W B.Approaches to reporting grade uncertainty in high nugget gold veins[J].Applied Earth Science，2012，121（1）：29-42.

[7]OLIVER M A，WEBSTER R.A tutorial guide to geostatistics：computing and modelling variograms and kriging[J].Catena，2014，113：56-69.

[8]ANNELS A E.Mineral deposit evaluation：a practical approach[M].London：Chapman and Hall，1991.

[9]ELLIOTT S M，SNOWDEN D V，BYWATER A，et al.Reconciliation of the McKinnons Gold Deposit，Cobar，New South Wales[M]∥EDWARDS A C.Mineral resource and ore reserve estimation—the AusIMM Guide to Practice.Victoria：The Australasian Institute of Mining and Metallurgy，2001：257-268.

[10]DUBRULE O.Estimating or choosing a geostatistical model[M]∥DIMITRAKOPOULOS R.Geostatistics for the next century.Springer：Dordrecht，1994：3-14.

[11]MARCOTTE D.Generalized crossvalidation for covariance model selection[J].Mathematical Geology，1995，27（5）：659-672.

[12]ISAAKS E H，SRIVASTAVA R M.An introduction to applied geostatistics[M].New York：Oxford University Press，1989.

[13]GUIBAL D.Variography，a tool for the resource geologist[M]∥ EDWARDS A C.Mineral resource and ore reserve estimation—the AusIMM Guide to good practice.Victoria：The AusIMM，2001：95-90.

[14]DOMINY S C，STEPHENSON P R，ANNELS A E.Classification and reporting of mineral resources for highnugget effect gold vein deposits[J].Exploration Mining Geology，2001，10（3）：215-233.

[15]CLARK I.Statistics or geostatistics？ Sampling error or nugget effect？[J].The Journal of the Southern African Institute of Mining and Metallurgy，2010，110（6）：307-312.

[16]BABAKHANI M，DEUTSCH C V.Compositing for the nugget effect[C]∥CCG.Annual report 14.Edmonton：CCG，2012：309.

[17]SINCLAIR A J，BLACKWELL G H.Applied mineral inventory estimation[M].Cambridge：Cambridge University Press，2004.

[18]SARKAR B C.Geostatistics in groundwater modelling[M]∥SIKDAR P K.Groundwater development and management.New Delhi：Capital Publishing Company，2019.

[19]高幫飞，沈阳，钟长汀，等.刚果（金）绿纱铜钴矿床黑色页岩Rb-Sr测年及其区域成矿意义[J].地质学报，2021，95（4）：1 029-1 049.

[20]高帮飞，谢徽，沈阳，等.一种确定资源储量估算的品位域的方法：CN201611040814.3[P].2017-05-31.

[21]ROSSI M E，DEUTSCH C V.Mineral resource estimation[M].Berlin：Springer，2014.

[22]高帮飞，陈志广，孙刚，等.内蒙古常福龙金矿床Au品位分布特征及其地质意义[J].黄金，2012，33（9）：9-12.

[23]SPRINGETT M.Sampling and ore reserve estimation for the Ortiz gold deposit，New Mexico[R].Rend：Nevada Bureau of Mines and Geology，1983：152-164.

[24]DOMINY S C，PLATTEN I M，RAINE M D.Grade and geological continuity in highnugget effect gold-quartz reefs：implications for resource estimation and reporting[J].Applied Earth Science，2003，112（3）：239-259.

[25]WACKEMAGEL H.Multivariate geostatistics：an introduction with applications（third，completely revised edition）[M].Berlin：Springer，2003.

[26]CARR J R.On visualization for assessing kriging outcomes[J].Mathematical Geology，2002，34（4）：421-432.

[27]DEUTSCH C V.Correcting for negative weights in ordinary kriging[J].Computers and  Geosciences，1996，22（7）：765-773.

[28]ARMSTRONG M.Basic linear geostatistics[M].Berlin：SpringerVerlag，1998.

[29]BAAFI E Y，KIM Y C，SZIDAROVSZKY F.On nonnegative weights of linear kriging estimation[J].Mining Engineering，1986，38：437-442.

[30]HOHN M E.Geostatistics and petroleum geology[M].Berlin：Springer，1988.

[31]BROOKER P I.A parametric study of robustness of kriging variance as a function of range and relative nugget effect for a spherical semivariogram[J].Berlin：Mathematical Geology，1986，18（5）：477-488.

[32]ABZALOV M Z.Geostatistical criteria for choosing optimal ratio between quality and quantity of the samples：method and case studies[C]∥AusIMM.Mineral resource and ore reserves estimation.Melbourne：AusIMM，2014：91-96.

[33]侯景儒，黃竞先.地质统计学及其在矿产储量计算中的应用[M].北京：地质出版社，1982.

[34]GRINGARTEN E，DEUTSCH C V.Teachers aide variogram interpretation and modeling[J].Mathematical Geology，2001，33（4）：507-534.

[35]高帮飞.资源量估算的边界分析与矿化体圈定[J].地质与勘探，2018，54（2）：415-425.

[36]李红兵，高帮飞.岩金矿床资源储量估算品位域的确定及其意义[J].黄金，2021，42（4）：6-11.

[37]COOMBES J.The art and science of resource estimation：a practical guide for geologists and engineers[M].Subiaco：Coombes Capability，2008.

Geological interpretation of nugget effect and its constraint on grade estimationGao Bangfei1，2，Li Hongbing3，Zhang Shuchen1，2，Chen Weikang1，2，Liu Guofeng4，Sun Gang1

（1.China Railway Resources Group Co.，Ltd.; 2.La Miniere de Kalumbuwe Myunga SAS;

3.Zijin Mining Co.，Ltd.，Kamoa Project; 4.Tenk Fungurume Mining SAS）

Abstract：The continuous evaluation of geology （mineralization） is the basis of mineral exploration and resource estimation.The nugget effect is the ratio of the nugget variance to the total variance in the variogram，which can be used to describe the variability of the spatial structure of geological variables and has important influence on grade estimation.In practice，however，the fitting of variogram and geological interpretation of nugget effect are subjective and arbitrary.Based on the previous studies，the paper mainly discussed the main factors influencing the nugget effect in variogram，systematically elucidated the indication of the nugget effect on geological （mineralization） continuity，and the significance on kriging and IDW grade estimation.The study is practical for mineral exploration evaluation and resource estimation to improve their reliability.

Keywords：variogram;nugget effect;screen effect;kriging;IDW