“确定起跑线”教学设计

李春梅

教学内容：

人教版数学六年级上册第80～81页综合实践。

教材分析：

本节课是在学生掌握了圆的概念和周长等知识的基础上进行设计的一节综合应用数学知识的实践活动课。这个数学综合实践活动，一方面让学生了解田径场跑道的结构，通过小组合作探究性活动，综合应用所学的知识和方法，动手实践解决问题，学会确定起跑线的方法;另一方面让学生体会数学在生活中无处不在，在各个领域，处处都能发现数学问题，培养学生用数学的眼光看待生活，发现生活中的数学问题的习惯，体会数学的应用价值，增强学生应用数学的意识，不断提高实践能力和解决问题的能力。

教学过程：

一、创设情境，引入新课

1.教师设问：同学们十二月是我们学校的什么节

预设生成：体育节。

教师引导：发扬奥运精神，从小热爱体育，咱们学校也积极响应。

2.创设情境：课件出示情境图，引导学生观察，获取信息

师：看，运动场上多热闹呀！这是100米跑起跑情景，这是400米跑起跑情景。教师提问：看了两幅图你有什么发现？

预设生成1：100米决赛起跑时，运动员是站在同一起跑线上的;400米决赛起跑时运动员是站在不同起跑线上的。

预设生成2：400米决赛起跑时，运动员一个比一个要往前移一些。

3.提出问题，引入新课

教师设疑：为什么400米决赛起跑时运动员会站在不同的起跑线上呢？

为了能让同学们比赛时公平、公正，体育老师在设计400米跑道时应该怎样确定起跑线？

这节课，我们就带着这些问题，走进运动场，一起探究确定起跑线。（板书：确定起跑线）

设计意图：此环节紧密联系学校十二月进行的“体育节”设问导入，创造这一生活化的教学情境，目的是激发学生的学习兴趣，唤起学生的学习经验，为新知探究找准了目标。

二、组织互动，探究新知

（一）组织自学，了解运动场的结构

1.组织自学：阅读课本第80、81页主题图，了解400m跑道的结构，整理获取的信息。

2.交流自学，了解跑道结构。

师：刚才同学们都进行了自学，老师想了解一下大家学得怎么样？

课件出示提纲：

（1）跑道由（   ）和（  ）组成。

（2）左右两个半圆形的弯道合起来刚好是（  ）。

（3）每一圈跑道的长度可以看成（  ）+（  ）。

师：同学们同意刚才几位同学的说法吗？

预设生成：同意。

师：课件演示，这是运动场的平面图，由里到外，每圈左右两边各是一个半圆，中间部分是两条直道，每一圈的直道部分是一样长的，我们把直道移开，把两边的半圆合在一起，就成了一个个同心圆，每相邻两个圆中间的部分是圆环，两个圆之间的距离在圆环上叫“环宽”，在这里我们把它称为“道宽”。因此，每圈跑道长=一个圆的周长+2条直道的长。

设计意图：对于运动场的结构，六年级的学生并不陌生，学生借助已有的知识经验可以自己学懂，留给学生一定的时间自学，可以让学生自主性得到充分发挥，同时也为后面的小组合作探究交流打下基础。

（二）组织合作探究

如何确定400米跑的起跑线？

教师引导：运动场跑道的结构我们了解清楚了，如果我们知道，运动场的直道长85.96m，最里圈半圆的直径是72.6m，每相邻两条跑道的道宽是1.25m（课件出示），那该如何确定400米赛跑的起跑线呢？同学们还想不想继续研究下去？

预设生成：想。

师：老师就把这个学习任务交给我们的学习小组去完成。

1.课件出示合作要求

（1）交流：每一跑道的直径、圆的周长、每圈的总长度分别用什么算式表示？填写在小组汇报单上。

……

（2）想一想，相邻两个跑道的周长差异是怎样形成的？与什么有关？与什么无关？

（3）讨论：怎样很快算出相邻两个跑道周长的差距？

2.组织小组活动

预设1：已知最里圈的直径是72.6m，那么第二圈的直径应该增减2个道宽，就是72.6+1.25×2;第三圈的直径应该增减4个道宽，就是72.6+1.25×4;第四圈的直径应该增减6个道宽，就是72.6+1.25×6……

预设2：因为圆的周长=直径×圆周率，因此左右两个半圆的长分别是

72.6π、（72.6+1.25×2）×π=72.6π+1.25×2×π、（72.6+1.25×4）×π=72.6π+1.25×4×π、（72.6+1.25×6）×π=72.6π+1.25×6×π……

预设3：每圈的总长度分别是：72.6π+85.96×2，72.6π+1.25×2×π+85.96×2，72.6π+1.25×4×π+85.96×2，72.6π+1.25×6×π+85.96×2，……

3.組织汇报交流

师：刚才各小组的交流、讨论都很热烈，哪位小组代表愿意把你们的学习成果分享给大家？看看哪几位是今天最出彩的小老师？

预设1：我们小组的结论是：每往外一圈，直径就增加1.25×2，也就是2个道宽;每相邻两条跑道的直径就相差1.25×2。（即：2个道宽的积）

预设2：我们还发现，从里圈到外圈，左右两个半圆的周长（也就是一个圆的周长），都有72.6π，是一个不变量，每相邻两个圆的周长就相差1.25×2×π。（即：2个道宽×π的积）

预设3：我们再看每圈跑道的总长，又发现每一圈总长都是一个圆的周长加2条直道的长，都有85.96×2，这也是一个不变量，说明每相邻两个跑道的总长，与直道无关。（教师板书：无关）再看算式的前面，都有72.6π，这也是一个不变量，第一跑道的72.6π，到第二跑道的72.6π+1.25×2×π，相差1.25×2×π，第二跑道的72.6π+1.25×2×π与第三跑道的72.6π+1.25×4×π也是相差1.25×2×π，第三跑道的72.6π+1.25×4×π与第四跑道的72.6π+1.25×6×π也是相差1.25×2×π。因此，我们可以得出每相邻两个跑道的总长与弯道有关。（教师板书：有关）每相邻两个跑道的总长都相差1.25×2×π，也就是2个道宽×π的积。

预设4：其实我们只要知道运动场的道宽就可以很快算出相邻两个跑道周长的差距。

同学们对我们小组的交流有什么意见吗？大家还有什么要补充的？

设计意图：自主探索、合作交流是学生学习数学的重要方式，究竟“如何确定起跑线呢？”学生有了这一疑问，教师放手给学生进行小组合作探究，在这个环节中留给学生充足的学习时间，体现了生生互动，互帮互学的教学理念。用算式表示计算结果，培养了学生符号化思考的能力，紧接着让小组代表上台展示交流，充分体现学生主体性，同时也体现学生是数学学习的主人，教师是数学学习的组织者、引导者与合作者。

（4）引导归纳结论

师：刚才上台汇报的两位同学真是今天最出彩的小老师。

我们知道了，相邻跑道起跑线相差都是：道宽×2×π。

从这里可以看出：起跑线的确定与什么关系最为密切？

预设：与跑道的宽度关系最为密切。

小结：同学们经过努力终于找到了确定起跑线的秘密！其实只要知道了跑道的宽度，就能确定起跑线的位置。

设计意图：以上三个环节是学生展示的舞台，作为合作者、引导者的教师适时点拨，目的是将教学的重难点进行梳理、规范。

（三）应用结论，解决疑问

师：现在我们能解决课前的疑问了吗？

1.为什么400米赛跑时运动员不站在同一起跑线上？

2.体育老师在设计400米赛跑的跑道时应该怎样确定起跑线？

预设1：因为400米跑道有弯道，也有直道。外圈的总长比内圈要长，所以运动员就要依次往前移一定的距离。如果站在同一起跑线上就不公平了。

预设2：体育老师在设计400米赛跑的跑道时先测量出跑道的道宽，然后用道宽×2×π，一道比一道提前（2道宽×π）米，起跑线就确定好了。

师：标准运动场一圈就是400米，在确定起跑线时要了解一下运动场标不标准，如果场地较小，需要测量出道宽、最里圈半圆的直径，每条直道的长，算一算一圈有多少米。

师：课前老师测量过了学校运动场的道宽是1米，设计400米赛跑时应该怎样确定起跑线？

预设1：1×2×3.14=6.28米，一个跑道与一个跑道依次往前移6.28米。

设计意图：学生带着疑问进入学习，经过一系列的学习活动后，进行解决，旨在体现数学学习的目的是解决生活中的实际问题，体现了数学的应用价值。

三、应用拓展

师：接下来老师要检验一下，同学们学得怎么样，敢接受挑战吗？

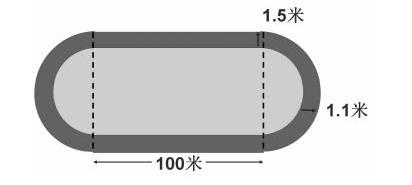
1.我能挑战：下图是某学校操场的跑道，进行400米的赛跑时，起跑线该依次提前多少米？如果道宽是1.1m呢？又该依次提前多少米？

2.拓展延伸：在本次体育节比赛中还有200米的比賽，跑道宽为1.25米，起跑线又该依次提前多少米？

设计意图：“我敢挑战”是结合本节课所学的知识点设计的，旨在检验学生对本节课知识的掌握情况。“拓展延伸”是促使学生灵活应用所学知识解决生活中的实际问题。

四、全课总结，提升认识

1.通过这节课的学习，你有什么收获？

生1：我学到了确定起跑线的方法。

生2：我知道400米跑道确定的起跑线的方法，还知道200米如何确定起跑线。

生3：我知道了只要知道跑道的宽，就可以确定400米、200米赛跑的起跑线。

2.你还有什么不懂的问题想和大家探讨？

预设：体育比赛中还有800m、1500m、3000m等赛跑，起跑线和400m赛跑一样吗？

师：是一样的，特别强调的是800m、1500m、3000m赛跑时，第一圈不能抢道，第二圈运动员就可以抢到最里圈跑了。

师：同学们，今天我们揭开了运动场的秘密，学会了确定起跑线的本领，大家自豪吗？运动会马上就到了，请大家踊跃到体育组报名，参加运动场的设计，用我们今天学到的知识，当好小小设计师。

设计意图：学生通过独立自学、合作探究、自主交流、学以致用几个环节的学习后进行总结评价，旨在将整节课知识点进行梳理、完善，使学生加深理解，鼓励学生活学活用。