基于灰色模型的衡阳市总家庭用水量预测分析

李思燕 罗清海 高瑞霞 谢勇

南华大学土木工程学院

有研究表明，从建筑全生命周期来看，运行使用阶段的建筑能耗占总建筑能耗的80%～90%，施工和拆除仅占10%～20%[1]。对于居住建筑而言，运行阶段的能耗主要为居民居住期间为满足生活需求而使用建筑而产生的能耗，主要包括用水、用电、用燃气等。随着社会经济发展，人民生活水平的提高，衡阳市近几年的总家庭用水量逐年增加。根据《衡阳统计年鉴2019》，2018 年自来水供水总量为17093.8 万m3，其中家庭总用水量为6659.2 万m3，占比达39%。在家庭用水方面，除了对水资源的消耗以外，加热冷水的能耗也占相当一部分比重，有调查统计热水能耗占住宅总能耗的12%[2]。因此，本文对家庭用水量进行预测，旨在一定程度上为家庭节水节能提供一定程度上的参考。并结合实地调研，对家庭用水节水提出几点建议。

1 灰色预测模型原理

灰色系统理论是由我国学者邓聚龙教授于1982年提出的一种解决具有较高灰性或不确定性贫信息问题的新方法，到目前为止已经发展成一套比较成熟的系统理论。灰色预测方法通过对原始数据的处理和灰色模型的建立，挖掘、发现、掌握系统演化规律，对系统的未来状态做出科学的定量预测[3]。灰色预测模型相比其他预测模型而言具有建模数据少、计算简单等优点，被广泛应用于各个领域：用水量预测[4]、电力需求预测[5]、煤炭消费量预测[6]、沉降预测[7]等。在灰色系统预测模型中，GM(1,1)模型的使用十分广泛。本文将建立新陈代谢GM(1,1)模型对衡阳市未来3 年的总家庭用水量进行预测。

1.1 均值GM(1,1)模型

均值GM(1,1)模型的建模原理如下：

1）设有原始序列X(0)=(x(0)(1)，x(0)(2)，…，x(0)(n))，对其进行一次累加计算，则X(0)的1-AGO 序列为：X(1)=(x(1)(1)，x(1)(2)，…，x(1)(n))。通过一次累加，可以使没有规律性的原始数据呈现出明显的增长规律性。

2）对序列X(1)施以紧邻均值生成算子，紧邻均值生成序列记为Z=(z(2)，z(3)，…，z(n))。其中z(k)=0.5x(k)+0.5x(k-1)，k=2，3，…，n。

1.2 新陈代谢GM(1,1)模型

将GM(1,1)模型的预测值x(0)(n+1)置入X(0)同时去掉老信息x(0)(1)，形成的新序列X(0)=(x(0)(2)，…，x(0)(n)，x(0)(n+1))。以此新序列建立的模型称为新陈代谢GM(1,1)模型。不断地对数据进行新陈代谢，就能依次得到新陈代谢GM(1,1)模型的预测值。随着系统的不断发展，老信息在系统中的作用逐渐减弱，及时去掉老信息能使建模序列更符合当前系统的运行特征。相比传统的GM(1,1)模型，能使预测结果更加精确。同时引入了缓冲算子，优化原始数据，提高模型精度。

1.3 模型检验

灰色系统模型的检验通常采用：残差检验、关联度检验以及后验差检验。一般情况下，残差检验是最常用的检验指标。下文对于模型精度的检验也将采用残差检验。常用的精度等级表见表1。

表1 精度检验等级参照表

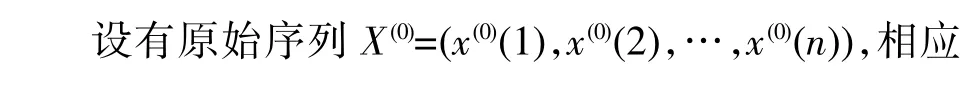
2 衡阳市总家庭用水量模拟

家庭用水跟人们生活息息相关，且户与户之间有时相差悬殊，有较大的节水潜力。如果能够对家庭用水量进行准确的预测，了解家庭用水量的发展趋势，相信能够一定程度上为家庭用水节水提供一定参考意义。目前，对于用水量的预测方法[8-11]中：指标分析法、神经网络法、回归分析法、灰色预测法等都是常用的预测方法。

影响家庭用水量的干扰因素有常住人口、收入情况、教育水平、节水理念、水价等，符合灰色系统理论“部分信息已知、部分信息未知”的不确定性系统概念。在各种影响因素中，以常住人口为例，其可能因为工作、学习等原因发生变化变成不确定的量。因此家庭用水量可以看成一个“部分信息明确、部分信息不明确”的灰色系统。有研究表明[12]：对于GM(1,1)模型而言，样本越小，模型效果越好。一般情况下，采用4 个数据进行GM(1,1)建模较好。因此本次模拟收集了衡阳市2014-2018 总家庭用水量数据（数据来源：衡阳统计年鉴2015-2019），见图1。由图可知，数据平滑度较好，呈现明显的增长规律，因此可以直接对数据进行建模。

图1 2014-2018 年衡阳市总家庭用水量

2.1 均值GM(1,1)模拟

以2014-2017 年的用水量数据进行GM (1,1)建模，以2019 年的数据作为预测结果对照组。对原始序列进行直接GM(1,1)建模。根据上文建模步骤进行建模，计算结果保留三位有效数字，计算结果具体如表2所示。

表2 均值GM(1,1)模拟结果

由计算结果得，均值GM (1,1) 的平均相对误差Δ=0.316%<1%，对照精度检验等级参照表可知精度等级为一级，精度等级高，可以用来预测。使用该模型预测2019 年总家庭用水量，得到数据为7041.984 万m3。将预测数据与2019 年实际用水数据6926 万m3对比可得预测误差为1.67%，偏差较小。因此均值GM(1,1)可以作为新陈代谢GM(1,1)的基础模型，用来对衡阳市未来家庭用水量进行预测。

2.2 新陈代谢GM(1,1)模拟分析

在以2015-2018 总家庭用水量数据建立的GM(1,1)模型上，加入2019 用水量数据同时剔除2015 年的用水量数据，对得到新序列进行建模。此时建立的模型为新信息GM(1,1)，模拟结果如表3 所示。计算得平均相对误差Δ=0.316%<1%属于一级精确度，预测结果可靠。

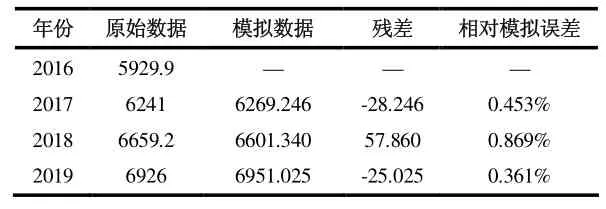
表3 新信息GM(1,1)模拟结果

以该模型作为基础模型对2020-2022 年衡阳市总家庭用水量进行预测。在数据序列中加入2020 年的预测值同时去掉2016 年作用数据，得到2021 年的预测值。如此对数据进行新陈代谢，来得到后一年的预测数据，预测结果如表4 所示。但必须要明确的是，灰色预测模型是基于对数据本身规律的挖掘，预测数据离最新数据越远其预测效果越差，即预测数据的个数越少其预测结果越可靠。最优做法为以2016-2019 年的数据建模预测2020 年的用水量，当2020 年的统计数据发布后，再以2017-2020 年的数据建模预测2021 年的用水量，依次不断更新数据库，摒弃老信息，能够得到比较准确的预测结果。

表4 2020-2022 总家庭用水量预测值

根据预测结果，从2020 年到2022 年的总家庭用水量呈现出逐年增高的趋势，至2022 年总家庭用水量将达到8057.299 万m3。这也意味着如果不采取任何节水措施，衡阳市家庭用水量在未来一段时间内将持续增长。

3 居民家庭用水调查与节水建议

3.1 居民家庭月用水量调查

就月用水量对衡阳市某一小区7 号楼进行调查，结果如图2，由图可知同一栋楼的月用水量存在较大差异。2019 年12 月，7 号楼用户最高月用水量为35 m3而最低用户月用水量仅为2 m3，该栋楼平均户用水量为12.8 m3。由此可见，对于家庭用水而言，其存在巨大的节能潜力。

图2 某小区7 号楼用户月用水量/m3

通过对一些住户的访谈了解到，大部分人在生活中没有节水习惯，用水模式以方便自己为主，不太考虑自身行为是否节水节能。比如洗水果时会直接打开水龙头冲洗而不是用盆子接水洗。当问及是否对用水节能采取措施时，部分人表示会购买节水型用水器具，极少人会对家庭用水二次利用。不过大部分人表示自己愿意接受节能教育。

3.2 居民家庭节水建议

Lutzenhiser&Bender[13]研究发现能源使用的39%取决于人的行为，因此在节水节能这条道路上切不可忽略“人”的作用。然而，国内的研究热点集中在“技术节能”，现状令人堪忧。以下从三个方面给出一些居民家庭用水的小建议。

从政府层面出发，政府作为人民的领导者具有一定的权威性，能够起到很好的模范带头作用。从居民的切身利益着手，让居民实实在在能感受到家庭节能所能带来的好处。由政府提出家庭节能的倡议，同时完善经济激励政策，如通过成立专项基金奖励节水效果显著的家庭。另一方面，继续实行阶梯水价收费标准，可适当提高基础水价、拉开阶梯水价差距。

从开发商层面，除了要加快节水产品的开发还应该加大推广力度。在推广产品时不应只向人们强调节能性能的好坏还应该加强对产品的正确使用方面。有研究表明家庭能源中有很大一部分能源的消耗是因为不正确的使用设备。宣讲产品时不能泛泛而谈，最好结合实际案例，用真实数据说话。让消费者通过案例感受到节水节能产品的优点，看到自己投下的资金能在一段时间以后得到回报。

从居民自身层面出发，要积极主动培养节水节能意识，改正不当的用水习惯。居民的节能意识是激发节能行为的内驱力。如果说经济激励措施的影响是短暂的，那么基于居民自身内驱力的节能行为则是稳定持续的。具备节能意识以后，随手关水龙头、用脸盘接水用、废水二次利用等将成为居民家庭“新常态”。

3 结论

1）通过2014-2017 年衡阳市家庭用水量数据对GM(1,1)模型进行模拟检验，结果表明均值GM(1,1)模拟精度高，预测结果偏差极小。在此基础上，使用新陈代谢GM(1,1)模型对衡阳市未来3 年的用水量进行预测，得到2020、2021、2022 年的家庭用水量分别为7319.234、7655.177、8057.299 万m3。预测结果显示，未来几年衡阳市家庭用水量将持续上升。

2）通过对衡阳市某小区7 号楼的月家庭用水量调查分析，得出了居民家庭用水存在巨大的节水节能潜力。

3）分别从政府层面、开发商层面和居民自身层面出发提出了几点有利于节水节能的建议。