基于IMM-UKF 的冷水机组故障检测与诊断

赵哲

西安建筑科技大学建筑设备科学与工程学院

0 引言

冷水机组一旦出现故障，会造成能源浪费、舒适度下降等诸多问题，因此需要对冷水机组进行故障检测与诊断。从现场应用的角度分析，现场机房内的冷水机组运行条件恶劣，其产生的运行数据会伴随着较大的噪声，会造成后续FDD 结果的误判，因此采用无迹卡尔曼滤波进行滤波去噪。从冷水机组的运行特点分析，冷水机组在实际运行中，并非一直处于正常模式下，若只建立正常模式下的UKF 来进行数据去噪，当冷水机组出现软故障时，单一模式下的UKF 必然会出现系统误差，从而不断累积，造成滤波发散，因此采用交互多模型来增强滤波的鲁棒性。

交互多模型在故障检测与诊断领域有着广泛的研究。Zhang[1]提出利用最大概率法来进行FDD，但建立的模型往往存在噪声及误差，这种方法会造成较高的虚警率。Willsky AS[2]提出最大似然比来判定是否发生故障，但是预测误差过大会造成似然比趋于无穷，不适合实际应用。Zhang[3]等人将似然比进一步改进，利用符号函数作为故障检测指标，利用联合指标来判定是否发生故障以及故障起始时间。本文基于上述的符号函数指标作出进一步改进，利用Tanh 函数作为故障检测指标，设置滑动窗口计算联合故障检测指标，从而进行FDD。相较于符号函数，采用Tanh 函数可以弱化故障模式模型概率与正常模式模型概率差值过小时对FDD 结果的影响，进一步降低虚警率。

1 模型建立

1.1 无迹卡尔曼滤波模型

假设有非线性离散系统的过程模型和量测模型：

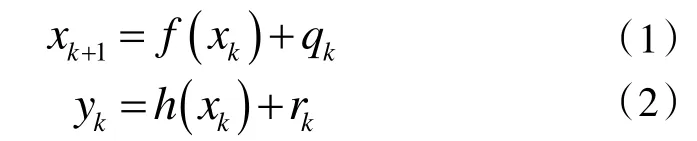
其中，k=1,2…，xk∊Rn为k时刻系统不可观测的状态向量；yk∊Rm为k时刻系统可观测的量测向量；qk-1∊Rn和rk∊Rm是相互独立的高斯白噪声，qk-1～N(0,Qk-1) 为过程噪声，表示xk-1变成xk过程中的不确定程度，rk～N(0,Rk)为量测噪声；f(·)和h(·)是已知的非线性函数。

无迹卡尔曼滤波可通过如下步骤实现[4]：

1）初始化

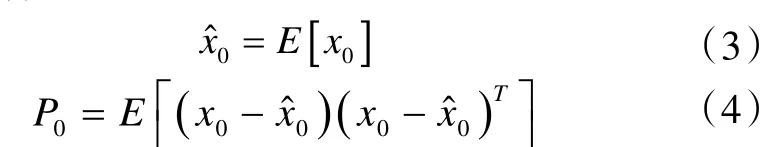
其中，x0表示系统的初始状态值表示先验均值；P0表示先验协方差矩阵。

2）状态向前一步预测

构造2L+1 个sigma 点：

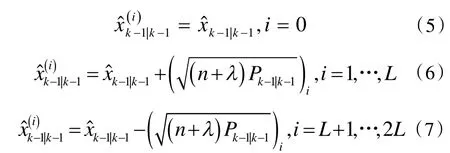
其中，λ为尺度参数，λ=α2(n+k)-n为标量参数，可以提高逼近精度。α决定采样点在周围的分布，通常设置为1>α>>0.0001；k是第二个尺度参数，在状态估计时通常设置为0，在参数估计是设置为3-n。适当调节α、k可以提高估计均值的精度。i表示sigma 点的第i列向量，共2L+1 个点。

将sigma 点代入非线性过程方程：

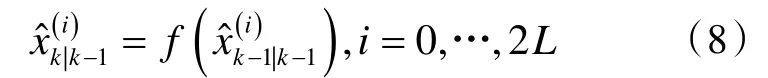
计算状态向量预测值为：

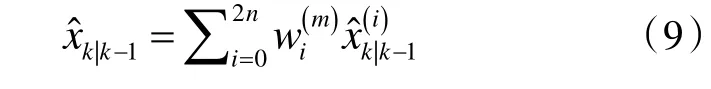
计算状态向量预测误差的协方差矩阵为：

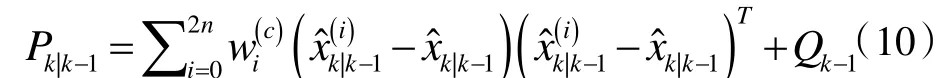
其中，wi(m)表示计算状态预测值的权重，wi(c)表示计算协方差矩阵的权重，具体可通过以下式表示：

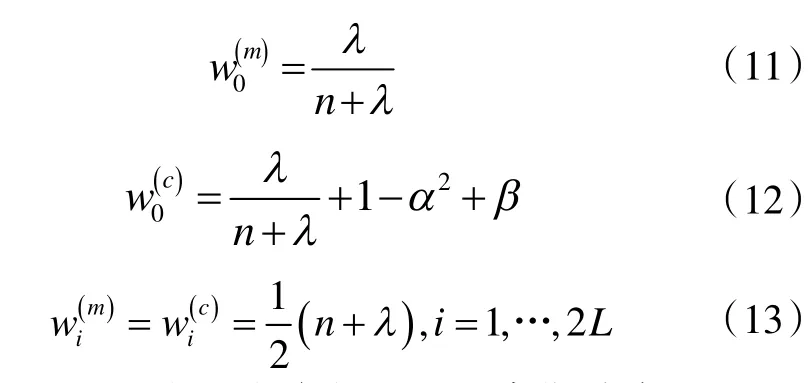
其中，β为状态分布参数，对于高斯分布，β=2 时最优；若状态变量为单变量，β=0 时最优。适当调节β可以提高方差的精度。

3）更新/纠错

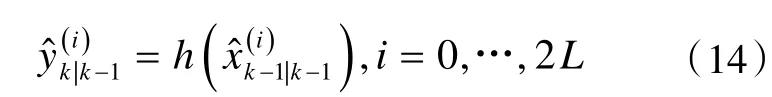
计算量测向量的预测值：

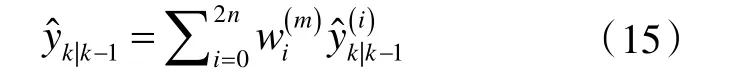
计算量测向量预测误差的协方差矩阵：

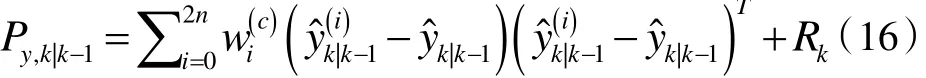
计算状态向量与量测向量之间的互协方差：

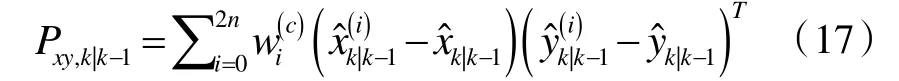
计算卡尔曼增益：

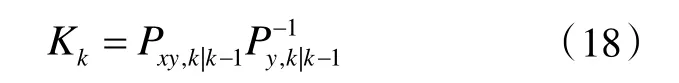
状态估计：

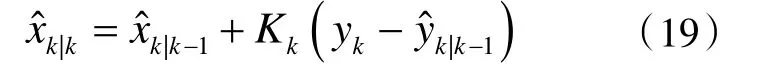
状态估计误差的协方差矩阵：

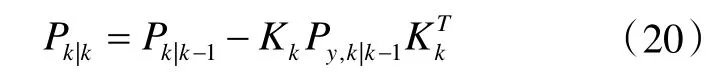
1.2 交互多模型

交互多模型算法最早由Blom 和Bar-Shalom[5]提出。IMM 并行运行多个子滤波器，每个滤波器对应一个系统模型。通过设置转移概率矩阵来控制不同模型间转换的概率，利用似然函数描述各个子滤波器的可靠度，结合这两者来实现每个子滤波器状态估计值的重新分配。IMM 输出的状态估计值是融合每个子滤波器输出值的加权和。

如图1 所示，IMM-UKF 算法分为初始化，更新模型概率，交互和状态融合四大步骤。

图1 IMM-UKF 流程图

初始化阶段需要定义马尔科夫转移矩阵Mar和模型概率初值由N×N个元素构成，每个元素mij表示从子滤波器i到子滤波器j的马尔科夫传递概率，i,j=1,2,…,N；模型概率反映k时刻时第j个子滤波器的可靠性。

更新模型概率阶段需要利用似然函数来分别量化第j个模型的似然性，从而实现由k-1 时刻模型概率到k时刻模型概率pjk的更新。

交互阶段会将第j个子滤波器在k-1 时刻输出的状态估计值和状态估计误差的协方差矩阵重新分配。通过预先设置的马尔科夫传递概率mij和k-1 时刻的归一化因子将k-1 时刻的模型概率pjk-1转化为k-1 时刻从第i个子滤波器到第j个子滤波器的交互概率，将此作为再分配的依据。

1.3 故障检测与诊断模型

Zhang[3]利用符号函数构建故障检测指标，该方法没有区分故障模式模型概率与正常模式模型概率之间差值的大小。因此，为降低检测虚警率、提高诊断正确率，引入Tanh 函数作为故障检测指标。如图所示，符号函数并没有区分故障模型概率与正常模型概率的差值对指标大小的影响。而对于Tanh 函数，当故障模式与正常模式之间模型概率的差值小时，Tanh 函数所计算的故障检测指标值就小；当故障模式与正常模式之间模型概率的差值越大，Tanh 函数故障检测指标值越趋近于±1。式（21）为基于Tanh 函数的故障检测指标。

图2 Tanh 函数和符号函数示意图

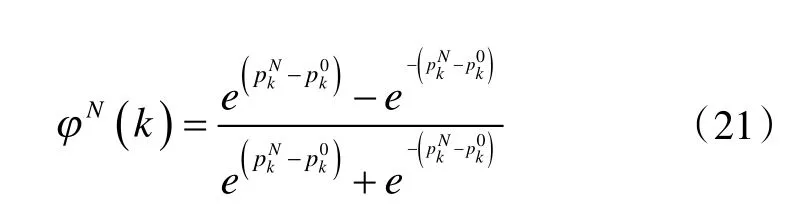
其中，pkN为第N个故障模式下k时刻的模型概率，pk0为正常模式下k时刻的模型概率，φN(k)表示k时刻第N个故障模式的故障检测指标。

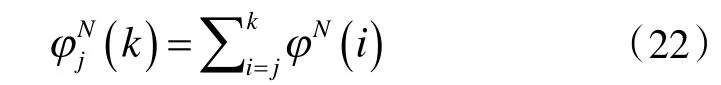
其中，j=k-H+1，k-H+2,…,k，H表示距离k时刻最近的滑动窗口大小，避免计算量过大。φNj(k)表示k时刻时滑动窗口H内的j时刻至k时刻的联合故障检测指标。

其中，λ代表阈值，若超过表示滑动窗口内发生该故障，且故障起始时刻j为滑动窗口内最大的联合故障检测指标。若滑动窗口内最大的联合故障检测指标未超过阈值，则说明滑动窗口内无故障发生。

2 研究对象

本文的研究对象为ASHRAE RP-1043 项目的实验数据。ASHRAE 项目是美国供暖、制冷和空调工程师协会对冷水机组FDD 展开的专项研究。RP-1043 实验采用一台90 冷吨离心式水冷冷水机组，蒸发器、冷凝器均为壳管式换热器，管程为水，制冷剂为R134a，冷却水流量FWC 为270 gpm，冷冻水流量FWE 为216 gpm[6]。该实验可以实时获取64 个变量，其中48个由传感器直接测得，16 个由软件实时计算得出，并且可以模拟出27 个运行工况和7 种典型故障模式，每种故障分为4 个劣化等级。8 种运行模式[7]分别是正常（Normal）、冷凝器结垢（CdFoul）、制冷剂充注过量（RefOver）、制冷剂泄漏（RefLeak）、不凝性气体（Ncg）、冷冻水流量减少（RedEW）、冷却水流量减少（RedCW）、润滑油过量（ExOil），对应的模型集合为{Nor，CF，RO，RL，Ncg，REW，RCW，EO}。

该实验的非线性离散系统模型常描述为：

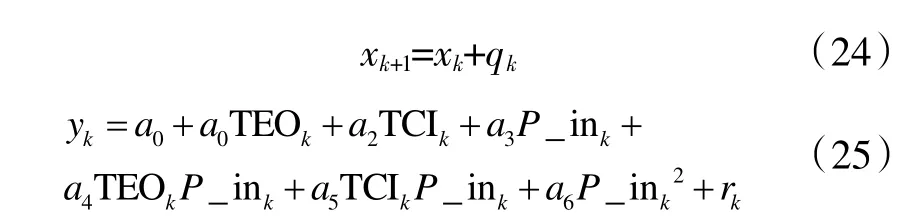
式（24）、（25）分别为冷水机组系统模型的状态转移方程和量测方程，a是经回归分析确定的参数，通常采用最小化总平方误差来对参数a进行寻优。状态参数设置为蒸发器出水温度TEO、冷凝器进水温度TCI和压缩机电机功率P_in，即：

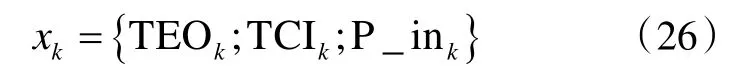
yk代表冷水机组的任一观测值，包括蒸发器进水温度TEI、冷凝器出水温度TCO、压缩机吸入温度T_suc、冷凝压力PRC、蒸发压力PRE、压缩机排放温度TR_dis，即：

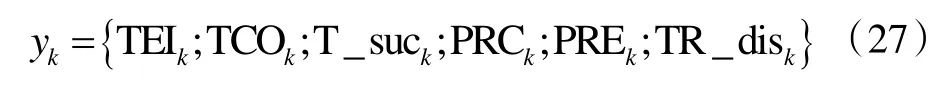
3 实验验证与分析

3.1 滤波方法对比分析

为了比较UKF 和IMM-UKF 两种滤波方法在变运行模式非线性系统中的性能，本文利用ASHRAE RP-1043 项目中变运行模式的实验数据进行验证。首先对冷水机组各个运行模式的系统离散模型进行拟合，得到各个运行模式下的无迹卡尔曼滤波器。其次，选择变运行模式下的冷水机组运行时间段对比两种方法的滤波效果，观察对比两种方法的滤波效果及RMSE 指标。

图3 可以看出，在变模式的运行状况下，由于UKF 采用单一模式建立的系统模型，因此并不适合其它模式下的状态估计，在运行模式改变后出现了严重的系统偏差，从而造成滤波发散。而IMM-UKF 基于8种运行模式的模型集建立8 个并行无迹卡尔曼子滤波器，具有更强地鲁棒性和适应性，因此始终保持良好的滤波精度。表1 可以看出IMM-UKF 相较于UKF 的RMSE 下降明显。对于状态估计值TEO、TCI、P_in，IMM-UKF 方法比UKF 方法的RMSE 分别下降了87.5%，74.2%和58.7%。结果表明，IMM-UKF 可以在改变运行模式的条件下显著降低滤波误差，有效抑制滤波发散问题。

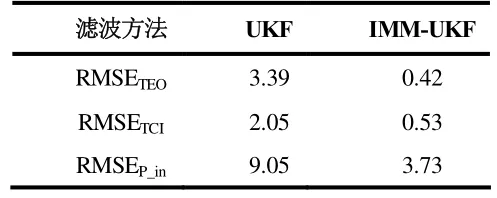
表1 各状态估计值不同滤波方法的RMSE 对比

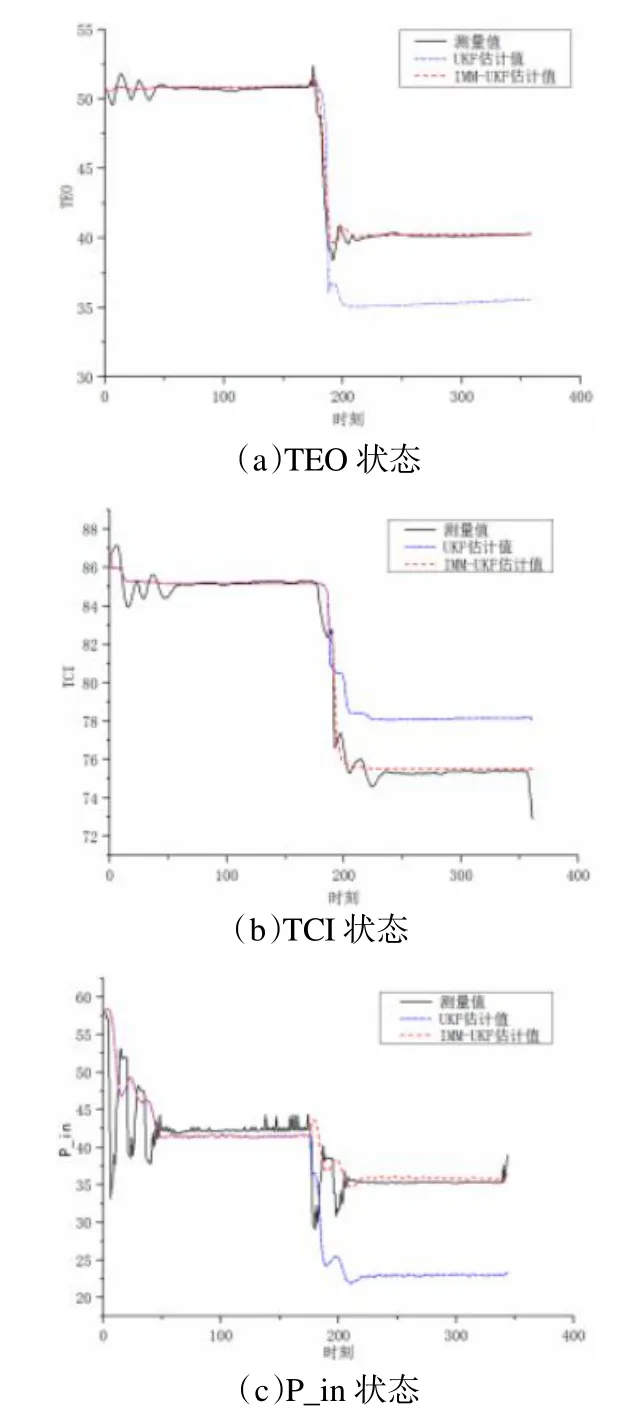
图3 变运行模式下各状态滤波效果对比

3.2 基于IMM-UKF 的FDD 评估

本次实验针对提出的Tanh 函数故障检测指标进行FDD 结果评估。本文将IMM-UKF 的FDD 框架按照故障检测指标的不同分为两个方案，方案一为基于符号函数故障检测指标的IMM-UKF FDD 框架；方案二为基于Tanh 函数故障检测指标的IMM-UKF FDD框架。在本实验中，将滑动窗口大小H设置为5，决策阈值λ设置为0。图4 表示两种方案的联合故障检测指标，横轴下方代表被检测为正常，横轴上方代表被检测为故障，真实故障起始时刻为30。图4 显示，方案一在故障时刻发生前一段时间就被误检测为故障，而方案二则更接近于真实故障的起始点。这说明方案一的符号函数故障检测指标未体现出故障模型概率与正常模型概率的差值对指标大小的影响，从而导致检测虚警率升高。而方案二的Tanh 函数故障检测指标针对故障模型概率与正常模型概率差值的大小会对应不同的值，当故障模型概率与正常模型概率差别不大时可以弱化对FDD 结果影响，从而降低检测虚警率。

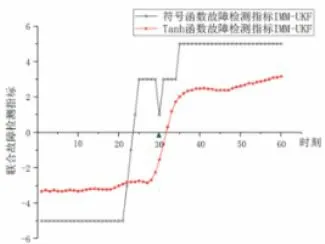
图4 两种方案的联合故障检测指标对比

图5 表示方案一和方案二的FDD 结果。横轴表示冷水机组的8 种运行模式，每种运行模式分别设置50 个样本点，纵轴表示FDD 结果。对比图5（a）和图5（b），可以直观地看出方案二虚警和误诊的数量普遍低于方案一，说明方案二的Tanh 函数故障检测指标的FDD 结果要优于方案一的符号函数故障检测指标。

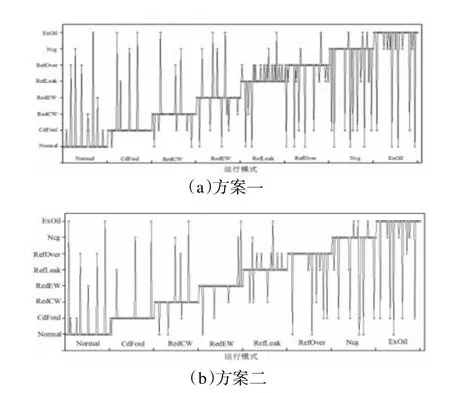
图5 两种方案的FDD 结果对比

图6 汇总了两种方案的检测正确率和诊断正确率。结果表明，方案一的FDD 结果均优于方案二的FDD 结果，说明在故障模型概率与正常模型概率差别不大的时刻，Tanh 函数故障检测指标通过弱化该时刻对FDD 结果的影响，可以有效地降低检测虚警率、提升诊断正确率。

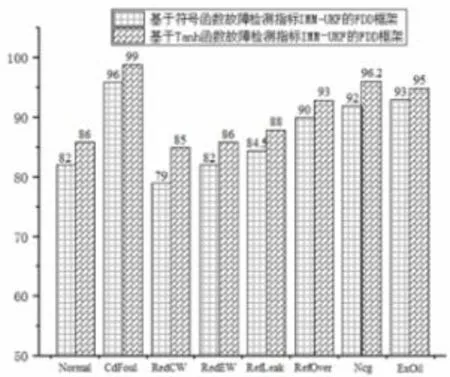
图6 两种方案的FDD 正确率对比

4 结论

为防止运行数据噪声对冷水机组FDD 结果的影响，本文提出基于IMM-UKF 的冷水机组FDD 框架。

1）通过建立8 种冷水机组运行模式的交互式无迹卡尔曼滤波，使得变运行模式阶段的滤波效果显著提升。相较于单模式的UKF，IMM-UKF 的三种状态估计值的RMSE 分别降低87.5%，74.2%和58.7%，有效抑制了滤波发散。

2）相比于符号函数故障检测指标，本文提出的Tanh 函数故障检测指标，衰减了在故障模型概率与正常模型概率差别不大时的故障检测指标，从而削弱其对FDD 结果的影响权重，有效提高FDD 正确率。