基于哈密顿原理的离散桥梁系统振动模态分析

□□ 王晓峰

(太原市市政公用工程质量安全站(太原市轨道交通建设服务中心)，山西 太原030024)

1 工程概况

鸭绿江界河公路大桥总长为1 266 m，主桥为双塔双索面钢箱梁斜拉桥，连续半漂浮体系。在86 m、229 m、636 m、229 m、86 m处分别布置18～23号桥墩；主梁采用正交异性钢桥面板扁平钢箱梁结构，梁高为3.5 m，宽为33.5 m，双索塔呈H型，高为194.6 m，采用箱形变截面；基础采用钻孔桩基础，辅助墩及过渡墩采用箱型墩。斜拉索为高强平行钢丝斜拉索，扇形布置，主梁上的标准索距为16.0 m，全桥为4组19对斜拉索，如图1所示。

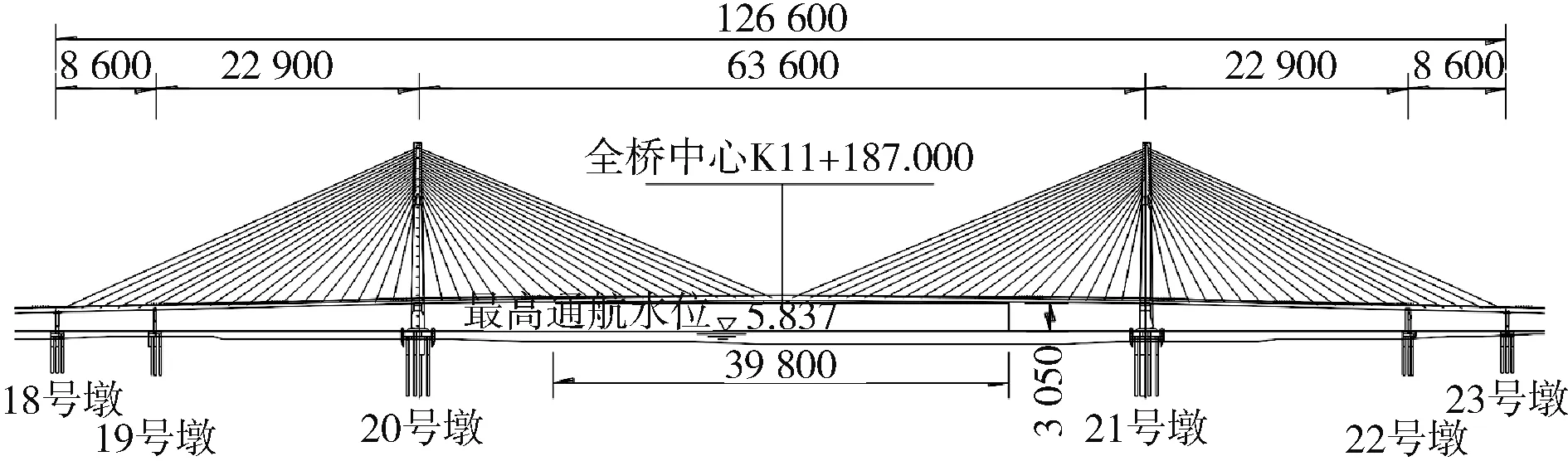
图1 鸭绿江界河公路大桥主桥总体布置(单位：cm)

双塔双索面钢箱梁斜拉桥的受力情况不同于普通桥梁，当荷载使桥梁顶端结构产生纵向弯曲变形时，主梁的横向弯曲变形不可忽略。常见的梁单元模型一般将结构刚度和质量集中于梁轴心线处，并认为受载后横断面保持不变，截面形状也保持不变[1-2]，所以常用的梁单元模型计算结果往往偏于保守[3-5]。根据盛春红等[6]研究结果表明，双塔双索面钢箱梁斜拉桥的整体振动形式是两边和中间会出现弯矩和位移峰值。因此，桥梁系统的离散化模型可简化表示为由两个弹性梁对称连接三个集中质量，而该系统属于三自由度系统。对于离散化模型的动力学建模一般可以采用拉格朗日方程或者哈密顿原理得到，这两种方法计算不需要过多的受力分析，对于复杂的力学问题计算过程更为方便。

2 离散桥梁系统动力学模型的建立

图2 离散桥梁系统简化模型

该系统可认为的典型的保守系统，系统的自由度为3，取广义坐标为y1、y2、y3。该系统的动能表示为：

(1)

系统在振动过程中会产生相对位移，取质量M的初始位置为重力势能的零势能面，弹性势能为kΔx2/2，重力势能为mgΔx，因而系统的势能可表示为：

mg(y1-y2)+mg(y3-y2)

(2)

根据式(1)和(2)，系统的拉格朗日函数可表示为：

2y22+y32-2y2(y1+y3)]-mg(y1-2y2+y3)

(3)

广义坐标y1、y2和y3所对应的广义动量分别表示为：

(4)

(5)

哈密顿函数为：

2y22+y32-2y2(y1+y3)]+mg(y1-2y2+y3)

(6)

因此，根据式(6)可得到广义坐标为y1、y2、y3所对应的哈密顿正则方程分别为：

(7a)

(7b)

(7c)

根据式(7)消去广义动量py1、py2和py3，得到离散桥梁系统的振动微分方程为：

(8)

其矩阵形式为：

(9)

式(9)为本文离散桥梁系统振动微分方程的矩阵表达形式。

3 离散桥梁系统的振动响应分析

3.1 振动频率

由式(9)可知离散桥梁系统的质量矩阵和刚度矩阵分别表示为：

(10)

考虑结构自由振动形式，代入频率方程|[k]-ω2[m]|=0可得：

(11)

展开式(11)得到系统的特征值分别为：

(12)

因此，系统的三阶固有频率分别为：

(13)

3.2 系统的正规坐标变换

根据式(13)，当ω1=0时，代入系统模态方程([k]-ω2[m])[φ]=0中，可得：

(14)

即为：

(15)

令φ11=1，则φ21=φ31=1，因此，ω1=0对应的归一化振型为：

(16)

(17)

(18)

(19)

(20)

根据式(16)、(18)和(20)得到系统的归一化振型为：

(21)

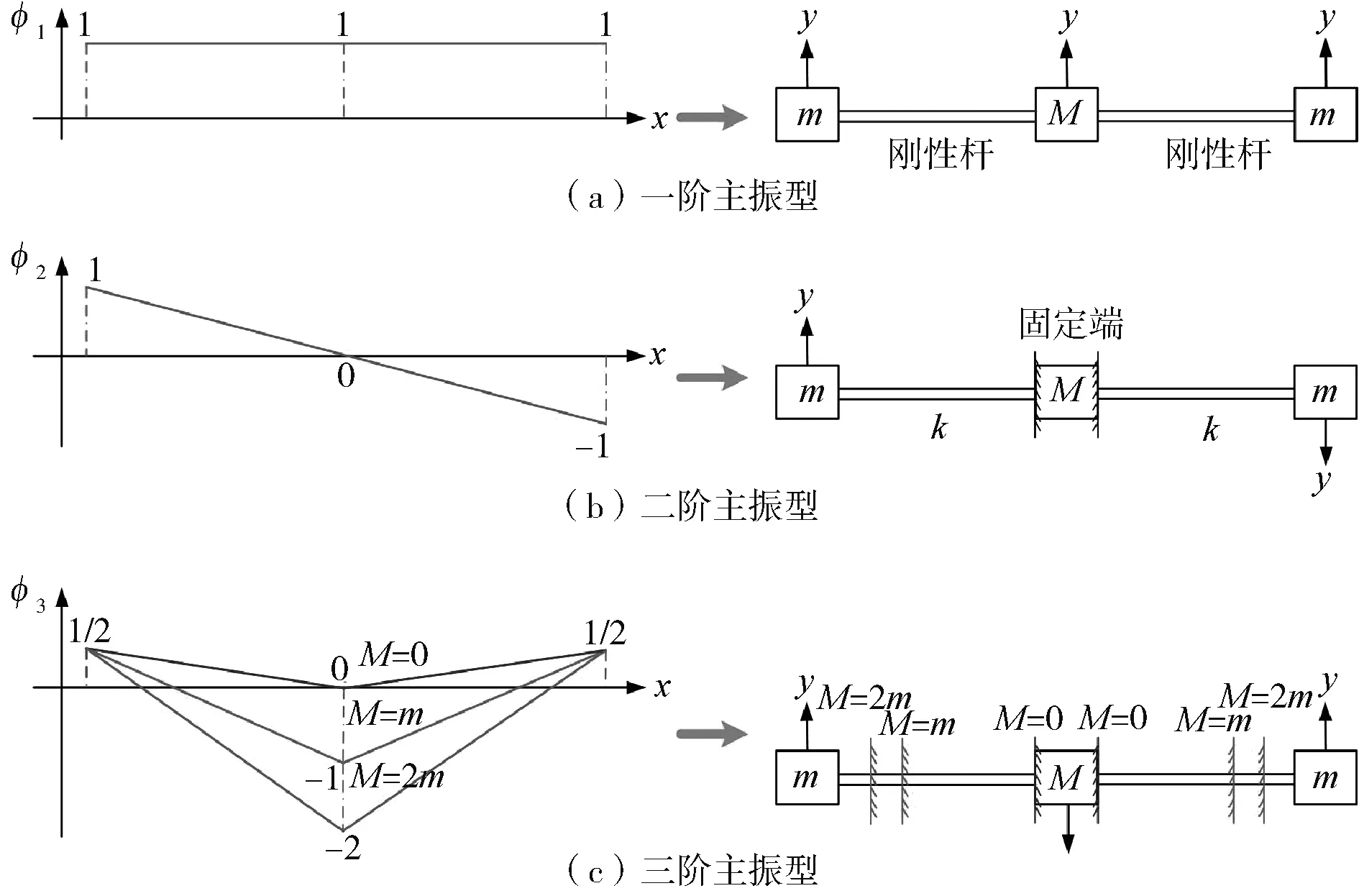
图3 离散桥梁系统的各阶主振型图和动力学等效图

图4为活载作用下主梁竖向位移的试验结果和理论结果对比图，并给出了主梁竖向位移随着边跨比(次边跨/边跨)的变化情况。随着边跨比的增加，主梁竖向位移先减小后增加，并且出现方向的反转现象。从图中可以看出，双塔双索面钢箱梁斜拉桥的整体振动形式是两边和中间会出现弯矩和位移峰值。本文中的理论结果与试验的变形模式结果相吻合。因此，通过对该桥梁进行一定的简化是可以通过理论来预测结构的振动位移。

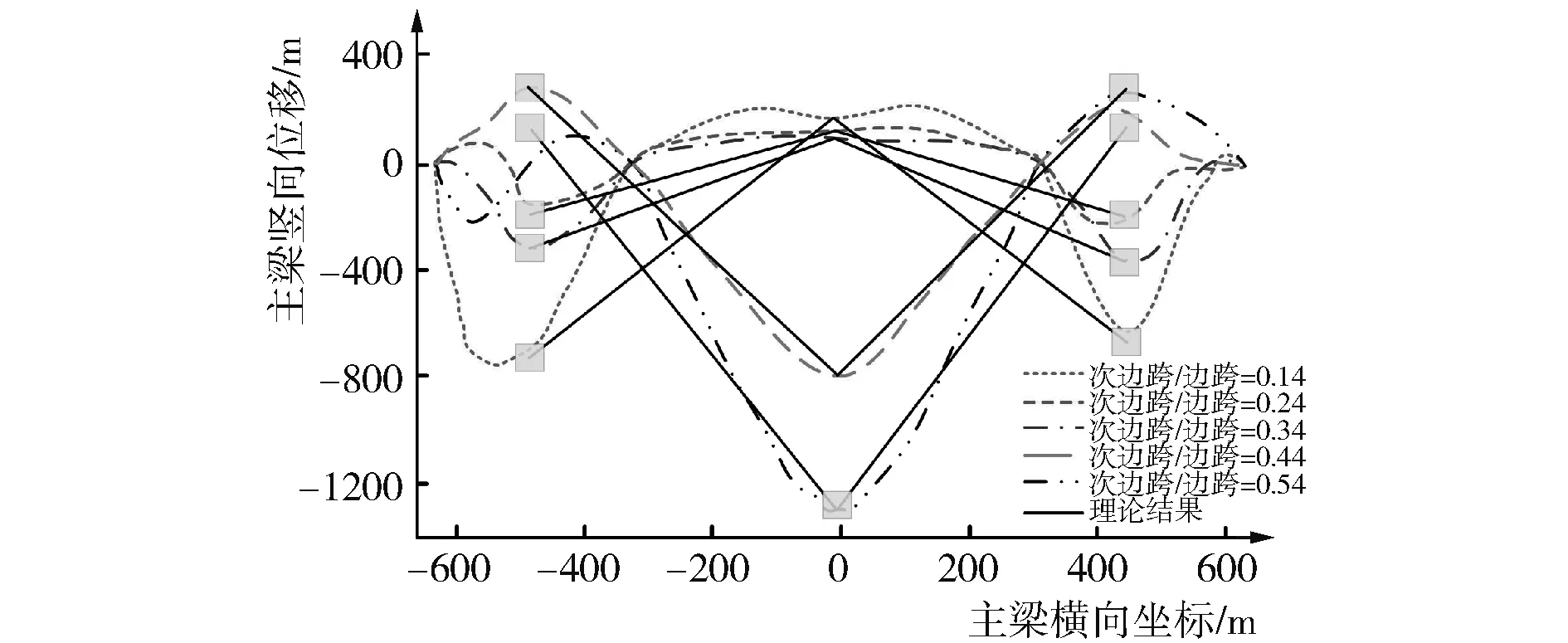
图4 活载作用下主梁竖向位移的试验结果和理论结果对比

此外，离散桥梁系统的主质量矩阵和主质量矩阵分别为：

[m*]=[φ]T[m][φ]

(22)

[k*]=[φ]T[k][φ]

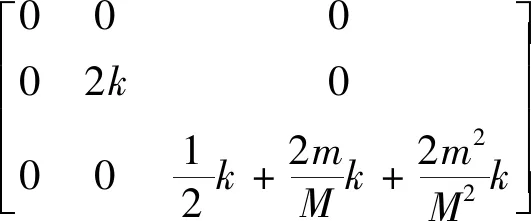
(23)

(24)

根据式(10)和(24)可得到正则后主质量矩阵和主刚度矩阵分别为：

(25)

(26)

根据式(25)和(26)，可得到正则后主质量矩阵为单位矩阵，主刚度矩阵为特征值矩阵。

4 结语

本文基于鸭绿江界河公路大桥工程实例得出桥梁整体的振动形式是两边和中间会出现弯矩和位移峰值，其他部位都是从最大值到0或者从0到最大值的过程。通过采用哈密顿正则方程得到离散桥梁系统的振动微分方程和三阶振动频率，得出离散桥梁系统的振动规律和节点位置分布情况，其理论结果与试验的变形模式结果相吻合。最后，对离散桥梁系统的振型进行了正规坐标变换。